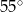Stosunek długości podstawy do ramienia trójkąta równoramiennego jest równy 2:3. Ramię jest nachylone do podstawy pod kątem  , takim, że
, takim, że
A) 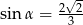 B)
B) 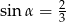 C)
C) 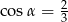 D)
D) 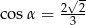
/Szkoła średnia/Zadania testowe/Geometria/Planimetria/Trójkąt/Równoramienny
Stosunek długości podstawy do ramienia trójkąta równoramiennego jest równy 4:3. Ramię jest nachylone do podstawy pod kątem  , takim, że
, takim, że
A) 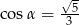 B)
B) 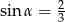 C)
C) 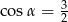 D)
D) 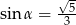
Stosunek długości podstawy do ramienia trójkąta równoramiennego jest równy 6:4. Ramię jest nachylone do podstawy pod kątem  , takim, że
, takim, że
A) 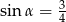 B)
B) 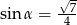 C)
C) 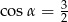 D)
D) 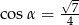
Dany jest trójkąt równoramienny 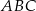 o kącie między ramionami
o kącie między ramionami 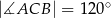 . Punkt
. Punkt 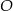 jest środkiem okręgu wpisanego w ten trójkąt. Prosta
jest środkiem okręgu wpisanego w ten trójkąt. Prosta 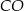 przecina podstawę
przecina podstawę 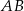 w punkcie
w punkcie 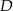 . Miara kąta
. Miara kąta 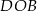 jest równa
jest równa
A) 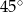 B)
B) 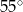 C)
C) 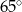 D)
D) 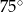
Dany jest trójkąt równoramienny 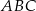 o kącie między ramionami
o kącie między ramionami 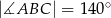 . Punkt
. Punkt 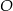 jest środkiem okręgu wpisanego w ten trójkąt. Prosta
jest środkiem okręgu wpisanego w ten trójkąt. Prosta 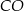 przecina podstawę
przecina podstawę 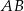 w punkcie
w punkcie 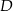 . Miara kąta
. Miara kąta 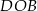 jest równa
jest równa
A) 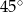 B)
B) 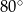 C)
C) 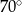 D)
D) 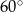
Dany jest trójkąt równoramienny 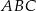 o kącie między ramionami
o kącie między ramionami 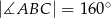 . Punkt
. Punkt 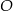 jest środkiem okręgu wpisanego w ten trójkąt. Prosta
jest środkiem okręgu wpisanego w ten trójkąt. Prosta 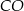 przecina podstawę
przecina podstawę 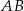 w punkcie
w punkcie 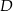 . Miara kąta
. Miara kąta 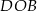 jest równa
jest równa
A) 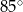 B)
B) 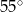 C)
C) 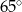 D)
D) 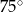
Ramię trójkąta równoramiennego 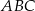 ma długość 8 cm i tworzy z podstawą kąt o mierze
ma długość 8 cm i tworzy z podstawą kąt o mierze 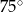 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 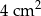 B)
B) 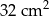 C)
C) 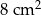 D)
D) 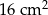
Dany jest trójkąt równoramienny, w którym ramię o długości 10 tworzy z podstawą kąt 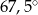 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 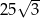 B)
B) 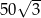 C)
C) 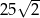 D)
D) 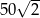
w trójkącie równoramiennym ramię ma długość 16 i tworzy z podstawą trójkąta kąt o mierze 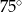 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 128 B) 64 C) 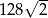 D)
D) 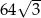
Dany jest trójkąt równoramienny, w którym ramię o długości 20 tworzy z podstawą kąt 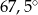 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 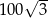 B)
B) 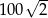 C)
C) 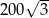 D)
D) 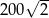
Dany jest trójkąt 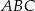 , w którym
, w którym 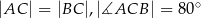 , zaś
, zaś 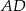 jest dwusieczną kąta
jest dwusieczną kąta 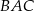 i
i 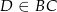 . Wówczas miara kąta
. Wówczas miara kąta 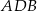 jest równa
jest równa
A) 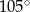 B)
B) 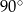 C)
C) 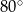 D)
D) 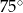
Dany jest trójkąt równoramienny 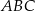 . Kąt
. Kąt 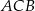 ma miarę
ma miarę 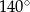 , a dwusieczna kąta
, a dwusieczna kąta 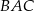 przecina bok
przecina bok 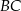 w punkcie
w punkcie 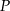 . Miara kąta
. Miara kąta 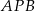 jest równa
jest równa
A) 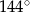 B)
B) 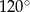 C)
C) 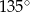 D)
D) 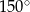
Dany jest trójkąt 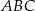 , w którym
, w którym 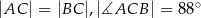 , zaś
, zaś 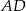 jest dwusieczną kąta
jest dwusieczną kąta 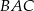 i
i 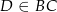 . Wówczas miara kąta
. Wówczas miara kąta 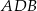 jest równa
jest równa
A) 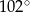 B)
B) 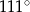 C)
C) 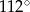 D)
D) 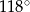
Dany jest trójkąt równoramienny 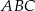 , w którym
, w którym 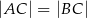 . Kąt między ramionami tego trójkąta ma miarę
. Kąt między ramionami tego trójkąta ma miarę 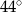 . Dwusieczna kąta poprowadzona z wierzchołka
. Dwusieczna kąta poprowadzona z wierzchołka  przecina bok
przecina bok 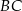 tego trójkąta w punkcie
tego trójkąta w punkcie 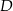 . Kąt
. Kąt 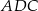 ma miarę
ma miarę
A) 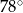 B)
B) 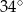 C)
C) 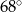 D)
D) 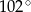
Dany jest trójkąt  , w którym
, w którym 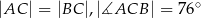 , zaś
, zaś 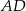 jest dwusieczną kąta
jest dwusieczną kąta 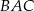 i
i 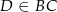 . Wówczas miara kąta
. Wówczas miara kąta 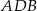 jest równa
jest równa
A) 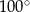 B)
B) 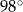 C)
C) 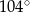 D)
D) 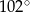
Dany jest trójkąt równoramienny 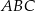 . Kąt
. Kąt 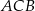 ma miarę
ma miarę 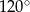 , a dwusieczna kąta
, a dwusieczna kąta 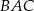 przecina bok
przecina bok 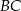 w punkcie
w punkcie 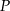 . Miara kąta
. Miara kąta 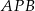 jest równa
jest równa
A) 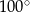 B)
B) 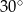 C)
C) 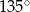 D)
D) 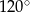
Dany jest trójkąt równoramienny, w którym ramię o długości 8 tworzy z podstawą kąt 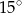 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 16 B) 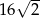 C)
C) 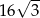 D) 32
D) 32
W trójkącie równoramiennym o polu 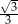 miara kąta przy podstawie jest równa
miara kąta przy podstawie jest równa 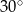 . Długość podstawy tego trójkąta jest liczbą
. Długość podstawy tego trójkąta jest liczbą
A) wymierną mniejszą od 2 B) niewymierną większą o 1
C) całkowitą większą od 1 D) niewymierną mniejszą od 2
W trójkącie równoramiennym o polu 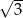 miara kąta przy podstawie jest równa
miara kąta przy podstawie jest równa 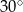 . Długość podstawy tego trójkąta jest liczbą
. Długość podstawy tego trójkąta jest liczbą
A) wymierną mniejszą od 3 B) niewymierną większą o 3
C) całkowitą większą od 3 D) niewymierną mniejszą od 3
W trójkącie równoramiennym o polu 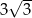 miara kąta przy podstawie jest równa
miara kąta przy podstawie jest równa 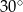 . Długość podstawy tego trójkąta jest liczbą
. Długość podstawy tego trójkąta jest liczbą
A) całkowitą większą od 4 B) niewymierną większą o 4
C) wymierną mniejszą od 4 D) niewymierną mniejszą od 4
Wysokość 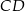 trójkąta równoramiennego
trójkąta równoramiennego 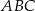 jest równa 8, a ramię
jest równa 8, a ramię 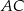 ma długość 10. Podstawa
ma długość 10. Podstawa 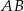 tego trójkąta ma długość
tego trójkąta ma długość
A) 12 B) 6 C) 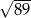 D)
D) 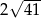
Wysokość 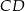 trójkąta równoramiennego
trójkąta równoramiennego 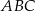 jest równa 10, a ramię
jest równa 10, a ramię 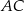 ma długość 14. Podstawa
ma długość 14. Podstawa 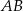 tego trójkąta ma długość
tego trójkąta ma długość
A) 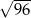 B)
B) 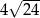 C)
C) 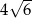 D)
D) 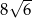
W trójkącie równoramiennym 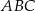 dane są
dane są 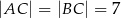 oraz wysokość
oraz wysokość 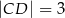 . Podstawa
. Podstawa 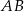 tego trójkąta ma długość
tego trójkąta ma długość
A) 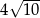 B)
B) 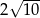 C)
C) 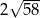 D) 10
D) 10
W trójkącie równoramiennym 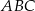 dane są
dane są 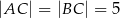 oraz wysokość
oraz wysokość 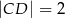 . Podstawa
. Podstawa 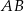 tego trójkąta ma długość
tego trójkąta ma długość
A) 6 B) 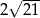 C)
C) 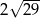 D) 14
D) 14
W trójkącie równoramiennym 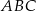 o podstawie
o podstawie 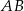 dane są:
dane są: 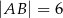 oraz
oraz 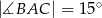 . Pole koła opisanego na tym trójkącie jest równe
. Pole koła opisanego na tym trójkącie jest równe
A) 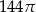 B)
B) 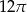 C)
C) 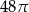 D)
D) 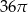
W trójkącie równoramiennym o bokach długości: 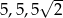 kąt przy podstawie ma miarę:
kąt przy podstawie ma miarę:
A) 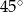 B)
B) 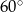 C)
C) 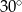 D)
D) 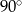
Na podstawie 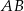 i ramieniu
i ramieniu 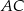 trójkąta równoramiennego
trójkąta równoramiennego 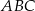 dane są punkty
dane są punkty 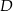 i
i 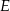 takie, że
takie, że 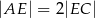 i
i 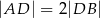 . Punkty
. Punkty 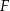 i
i 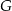 leżą na ramieniu
leżą na ramieniu 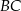 tak, że odcinki
tak, że odcinki 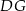 i
i 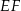 są prostopadłe do prostej
są prostopadłe do prostej 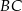 (zobacz rysunek).
(zobacz rysunek).
Pole trójkąta 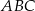 jest równe 18. Zatem suma pól trójkątów
jest równe 18. Zatem suma pól trójkątów 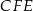 i
i 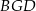 jest równa
jest równa
A) 9 B) 6 C) 3 D) 2
Punkty  i
i  są środkami odpowiednio podstawy
są środkami odpowiednio podstawy 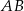 i ramienia
i ramienia 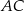 trójkąta równoramiennego
trójkąta równoramiennego 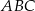 . Punkty
. Punkty 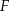 i
i 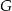 leżą na ramieniu
leżą na ramieniu 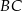 tak, że odcinki
tak, że odcinki 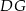 i
i 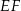 są prostopadłe do prostej
są prostopadłe do prostej 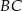 (zobacz rysunek).
(zobacz rysunek).
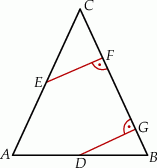
Pole trójkąta  jest równe 2, a pole trójkąta
jest równe 2, a pole trójkąta  jest równe 4. Zatem pole trójkąta
jest równe 4. Zatem pole trójkąta 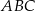 jest równe
jest równe
A) 24 B) 8 C) 12 D) 16
Każde z ramion trójkąta równoramiennego ma długość 20. Kąt zawarty między ramionami tego trójkąta ma miarę 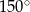 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 100 B) 200 C) 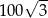 D)
D) 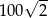
Każde z ramion trójkąta równoramiennego ma długość 20. Kąt zawarty między ramionami tego trójkąta ma miarę 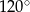 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 100 B) 200 C) 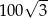 D)
D) 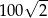
Pole powierzchni trójkąta równoramiennego o ramionach długości 6 cm i kącie między nimi 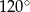 jest równe
jest równe
A) 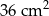 B)
B) 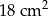 C)
C) 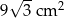 D)
D) 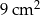
Ramię trójkąta równoramiennego 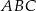 ma długość 8, a jeden z kątów tego trójkąta ma miarę
ma długość 8, a jeden z kątów tego trójkąta ma miarę 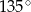 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 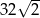 B)
B) 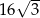 C) 32 D)
C) 32 D) 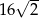
W trójkącie 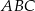 , w którym
, w którym 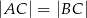 , na boku
, na boku 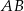 wybrano punkt
wybrano punkt 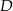 taki, że
taki, że 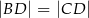 oraz
oraz 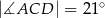 (zobacz rysunek).
(zobacz rysunek).
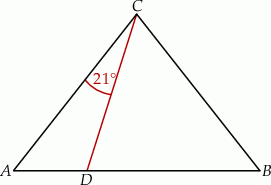
Wynika stąd, że kąt 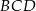 ma miarę
ma miarę
A) 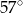 B)
B) 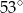 C)
C) 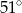 D)
D) 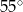
Dany jest trójkąt równoramienny 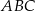 , w którym
, w którym 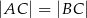 . Na podstawie
. Na podstawie 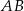 tego trójkąta leży punkt
tego trójkąta leży punkt 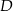 , taki że
, taki że 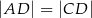 ,
, 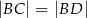 oraz
oraz 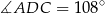 (zobacz rysunek).
(zobacz rysunek).
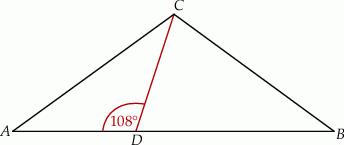
Wynika stąd, że kąt 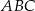 ma miarę
ma miarę
A) 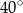 B)
B) 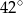 C)
C) 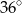 D)
D) 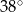
Dany jest trójkąt równoramienny 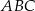 , w którym
, w którym 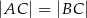 . Na podstawie
. Na podstawie 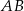 tego trójkąta leży punkt
tego trójkąta leży punkt 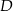 , taki że
, taki że 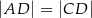 ,
, 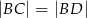 oraz
oraz 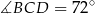 (zobacz rysunek).
(zobacz rysunek).
Wynika stąd, że kąt  ma miarę
ma miarę
A) 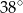 B)
B) 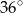 C)
C) 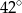 D)
D) 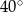
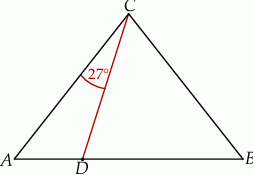
W trójkącie 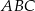 , w którym
, w którym 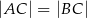 , na boku
, na boku 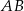 wybrano punkt
wybrano punkt 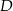 taki, że
taki, że 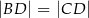 oraz
oraz 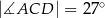 (zobacz rysunek).
(zobacz rysunek).
Wynika stąd, że kąt 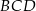 ma miarę
ma miarę
A) 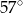 B)
B) 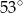 C)
C) 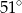 D)
D)