Wielomian 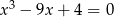 ma 3 pierwiastki rzeczywiste.
ma 3 pierwiastki rzeczywiste.
- Oblicz sumę odwrotności tych pierwiastków.
- Ustal, ile jest pierwiastków dodatnich.
- Oblicz odwrotność sumy kwadratów pierwiastków.
- Oblicz sumę kwadratów odwrotności tych pierwiastków.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wielomian 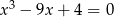 ma 3 pierwiastki rzeczywiste.
ma 3 pierwiastki rzeczywiste.
Wykaż, że równanie 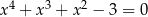 ma tylko jedno rozwiązanie które jest liczbą wymierną.
ma tylko jedno rozwiązanie które jest liczbą wymierną.
Rozwiąż równanie 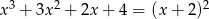 .
.
Rozwiąż równanie 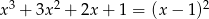 .
.
Rozwiąż równanie 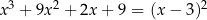 .
.
Rozwiąż równanie 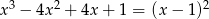 .
.
Rozwiąż równanie 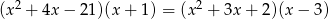 .
.
Rozwiąż równanie 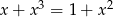 .
.
Rozwiąż równanie 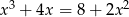 .
.
Wykaż, że równanie 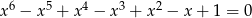 nie ma rozwiązań rzeczywistych.
nie ma rozwiązań rzeczywistych.
Dla jakich wartości parametru 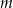 równanie
równanie 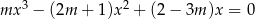 ma rozwiązania, których suma jest dodatnia?
ma rozwiązania, których suma jest dodatnia?
Wyznacz te wartości parametru 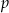 , dla których równanie
, dla których równanie 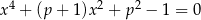 ma dokładnie dwa różne pierwiastki.
ma dokładnie dwa różne pierwiastki.
Wyznacz te wartości parametru 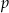 , dla których równanie
, dla których równanie 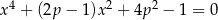 ma dokładnie dwa różne pierwiastki rzeczywiste.
ma dokładnie dwa różne pierwiastki rzeczywiste.
Dla jakich wartości parametru 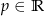 równanie
równanie 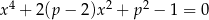 ma dokładnie dwa różne rozwiązania?
ma dokładnie dwa różne rozwiązania?
Rozwiąż równanie 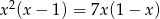 .
.
Rozwiąż równanie 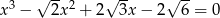 .
.
Rozwiąż równanie 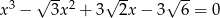 .
.
Wyznacz wszystkie wartości parametru 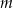 , dla których równanie
, dla których równanie
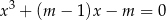
ma dokładnie dwa pierwiastki rzeczywiste. Dla otrzymanych wartości 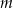 wyznacz te pierwiastki.
wyznacz te pierwiastki.
Wielomian 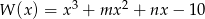 ma trzy pierwiastki
ma trzy pierwiastki 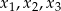 , przy czym
, przy czym 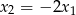 i
i 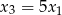 . Wyznacz
. Wyznacz 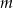 i
i  .
.
Wielomian 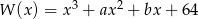 ma trzy pierwiastki:
ma trzy pierwiastki: 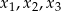 , przy czym
, przy czym 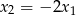 i
i 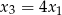 . Wyznacz
. Wyznacz  i
i 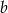 .
.
Równanie 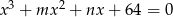 ma trzy pierwiastki będące kolejnymi wyrazami ciągu geometrycznego o ilorazie
ma trzy pierwiastki będące kolejnymi wyrazami ciągu geometrycznego o ilorazie 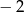 . Wyznacz
. Wyznacz 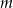 i
i  .
.
Rozwiąż równanie 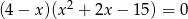 .
.
Rozwiąż równanie 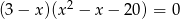 .
.
Znajdź wielomian o współczynnikach całkowitych, którego pierwiastkiem jest liczba 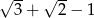 .
.
Liczba 3 jest pierwiastkiem wielomianu 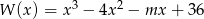 . Wyznacz parametr
. Wyznacz parametr 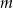 i pozostałe pierwiastki tego wielomianu.
i pozostałe pierwiastki tego wielomianu.
Rozwiąż równanie 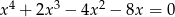 .
.
Rozwiąż równanie 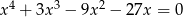 .
.
Rozwiąż równanie 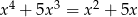 .
.
Funkcja 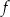 jest określona wzorem
jest określona wzorem 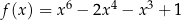 dla każdego
dla każdego 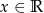 . Wykaż, że liczba 5 należy do zbioru wartości tej funkcji.
. Wykaż, że liczba 5 należy do zbioru wartości tej funkcji.
Dany jest wielomian 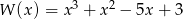 .
.
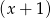 .
. 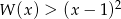 .
.Wielomian 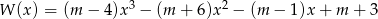 jest podzielny przez dwumian
jest podzielny przez dwumian 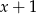 . Dla jakich wartości parametru
. Dla jakich wartości parametru 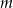 wielomian
wielomian 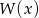 ma dokładnie dwa pierwiastki?
ma dokładnie dwa pierwiastki?
Dla jakich wartości parametru 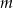 wielomian
wielomian 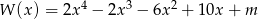 ma pierwiastek trzykrotny?
ma pierwiastek trzykrotny?
