Wykaż, że równanie 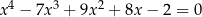 ma w przedziale
ma w przedziale 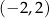 co najmniej dwa różne rozwiązania.
co najmniej dwa różne rozwiązania.
/Szkoła średnia/Równania/Wielomianowe
Wiedząc, że suma kwadratów pierwiastków równania
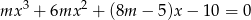
jest równa 30, wyznacz 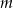 .
.
Sprawdź dla jakiego 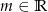 pierwiastki wielomianu
pierwiastki wielomianu 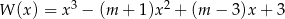 tworzą ciąg arytmetyczny?
tworzą ciąg arytmetyczny?
Wyznacz wszystkie wartości parametru 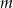 , dla których jedynym rozwiązaniem rzeczywistym równania
, dla których jedynym rozwiązaniem rzeczywistym równania 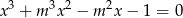 jest liczba 1.
jest liczba 1.
Wykaż, że jeżeli 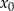 jest rozwiązaniem równania
jest rozwiązaniem równania 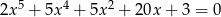 , to
, to 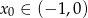 .
.
Rozwiąż równanie 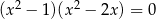 .
.
Rozwiąż równanie 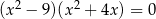 .
.
Rozwiąż równanie 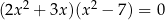 .
.
Rozwiąż równanie 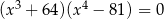 .
.
Rozwiąż równanie 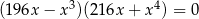 .
.
Rozwiąż równanie 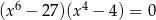 .
.
Dany jest wielomian 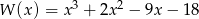 .
.
- Wyznacz pierwiastki tego wielomianu.
- Sprawdź, czy wielomiany
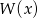 i
i 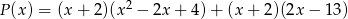 są równe.
są równe. - Uzasadnij, że jeśli
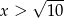 , to
, to 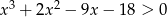 .
.
Rozważmy równanie 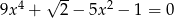 .
.
- Uzasadnij, że równanie to ma 4 pierwiastki.
- Oblicz sumę szóstych potęg wszystkich pierwiastków tego równania.
Liczby 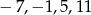 są miejscami zerowymi wielomianu czwartego stopnia
są miejscami zerowymi wielomianu czwartego stopnia 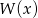 . Wykaż, że dla dowolnej liczby rzeczywistej
. Wykaż, że dla dowolnej liczby rzeczywistej  spełniona jest równość
spełniona jest równość 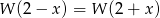 .
.
Rozwiąż równanie 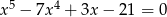 .
.
Rozwiąż równanie 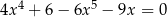 .
.
Uzasadnij, że jeżeli współczynniki wielomianu 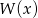 są liczbami całkowitymi i
są liczbami całkowitymi i 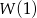 jest liczbą nieparzystą, to liczba nieparzysta nie jest pierwiastkiem wielomianu
jest liczbą nieparzystą, to liczba nieparzysta nie jest pierwiastkiem wielomianu 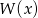 .
.
Pierwiastkiem wielomianu 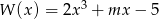 jest liczba -2. Wyznacz parametr
jest liczba -2. Wyznacz parametr 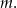
Pierwiastkiem wielomianu 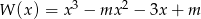 jest liczba
jest liczba 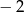 . Wyznacz parametr
. Wyznacz parametr 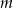 .
.
Dane są liczby wymierne 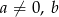 i
i 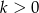 takie, że liczby
takie, że liczby 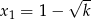 i
i 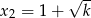 są pierwiastkami równania
są pierwiastkami równania 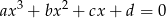 . Wykaż, że
. Wykaż, że  i
i 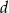 są liczbami wymiernymi.
są liczbami wymiernymi.
Dla jakich wartości parametru 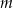 równanie
równanie 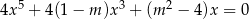 ma dokładnie trzy różne rozwiązania?
ma dokładnie trzy różne rozwiązania?
Dla jakich wartości parametru 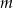 równanie
równanie ![2 2 (x − m ) [m(x − m ) − m − 1]+ 1 = 0](https://img.zadania.info/zad/3650840/HzadT1x.gif) ma więcej pierwiastków dodatnich niż ujemnych?
ma więcej pierwiastków dodatnich niż ujemnych?
Dany jest wielomian 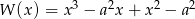 , gdzie
, gdzie 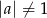 .
.
- Oblicz sumę pierwiastków tego wielomianu.
- Wyznacz wartość parametru
 , dla której suma kwadratów pierwiastków wielomianu
, dla której suma kwadratów pierwiastków wielomianu 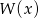 jest możliwie najmniejsza.
jest możliwie najmniejsza.
Rozwiąż równanie 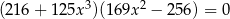 .
.
Rozwiąż równanie
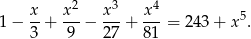
Dany jest wielomian 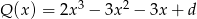 .
.
- Liczba 1 jest pierwiastkiem tego wielomianu. Oblicz
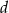 .
. - Dla
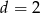 przedstaw wielomian
przedstaw wielomian 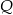 w postaci iloczynu wielomianów stopnia pierwszego.
w postaci iloczynu wielomianów stopnia pierwszego.
Wyznacz współczynniki  i
i 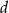 wielomianu
wielomianu 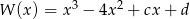 wiedząc, że liczba 1 jest dwukrotnym pierwiastkiem wielomianu
wiedząc, że liczba 1 jest dwukrotnym pierwiastkiem wielomianu 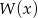 .
.

