Wartość wielomianu 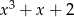 dla argumentu
dla argumentu 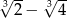 jest równa
jest równa
A) 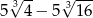 B)
B) 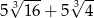 C)
C) 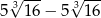 D)
D) 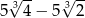
/Szkoła średnia/Zadania testowe/Funkcje/Wielomiany/Jeden wielomian
Dany jest wielomian 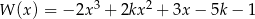 gdzie
gdzie 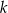 jest pewną liczbą rzeczywistą. Wiadomo, że liczba
jest pewną liczbą rzeczywistą. Wiadomo, że liczba 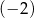 nie jest pierwiastkiem tego wielomianu. Zatem
nie jest pierwiastkiem tego wielomianu. Zatem
A) 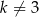 B)
B) 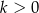 C)
C) 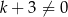 D)
D) 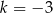
Wartość wielomianu 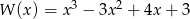 w punkcie
w punkcie 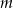 jest równa 15 dla
jest równa 15 dla
A) 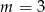 B)
B) 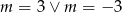 C)
C) 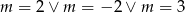 D)
D) 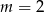
Wartość wielomianu 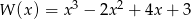 w punkcie
w punkcie  jest równa 11 dla
jest równa 11 dla
A) 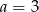 B)
B) 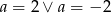 C)
C) 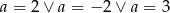 D)
D) 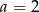
Wartość wielomianu 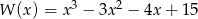 w punkcie
w punkcie 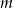 jest równa 3 dla
jest równa 3 dla
A) 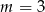 B)
B) 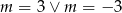 C)
C) 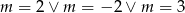 D)
D) 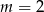
Wielomian 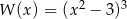 jest równy wielomianowi
jest równy wielomianowi
A) 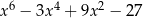 B)
B) 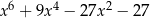
C) 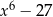 D)
D) 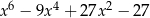
Funkcja 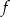 określona jest wzorem
określona jest wzorem 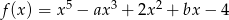 . Jeżeli
. Jeżeli 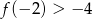 , to
, to
A) 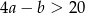 B)
B) 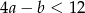 C)
C) 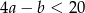 D)
D) 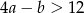
Wielomian 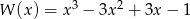
A) można przedstawić w postaci iloczynu trzech jednakowych czynników
B) dla argumentu 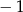 przyjmuje wartość
przyjmuje wartość 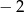
C) wartość równą 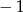 przyjmuje dla trzech argumentów
przyjmuje dla trzech argumentów
D) ma trzy różne pierwiastki
Wielomian 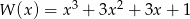
A) można przedstawić w postaci iloczynu trzech jednakowych czynników
B) dla argumentu 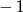 przyjmuje wartość
przyjmuje wartość 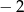
C) wartość równą 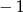 przyjmuje dla trzech argumentów
przyjmuje dla trzech argumentów
D) ma trzy różne pierwiastki
Wielomian 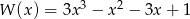
A) można przedstawić w postaci iloczynu trzech jednakowych czynników
B) dla argumentu 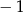 przyjmuje wartość
przyjmuje wartość 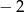
C) wartość równą 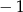 przyjmuje dla czterech argumentów
przyjmuje dla czterech argumentów
D) ma trzy różne pierwiastki
Stopień wielomianu 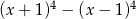 jest równy
jest równy
A) 4 B) 3 C) 2 D) 1
Wiadomo, że 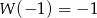 , gdy
, gdy 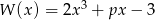 . Zatem wartość współczynnika
. Zatem wartość współczynnika 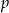 wynosi:
wynosi:
A) 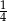 B) -4 C) 4 D) -1
B) -4 C) 4 D) -1
Dany jest wielomian 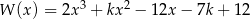 gdzie
gdzie 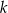 jest pewną liczbą rzeczywistą. Wiadomo, że liczba
jest pewną liczbą rzeczywistą. Wiadomo, że liczba 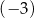 jest pierwiastkiem tego wielomianu. Liczba
jest pierwiastkiem tego wielomianu. Liczba 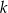 jest równa
jest równa
A) 2 B) 3 C) 6 D) 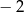
Dany jest wielomian 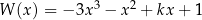 , gdzie
, gdzie 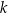 jest pewną liczbą rzeczywistą. Wiadomo, że wielomian
jest pewną liczbą rzeczywistą. Wiadomo, że wielomian 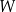 można zapisać w postaci
można zapisać w postaci 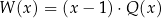 dla pewnego wielomianu
dla pewnego wielomianu 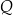 . Liczba
. Liczba 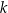 jest równa
jest równa
A) 29 B) 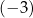 C) 0 D) 3
C) 0 D) 3
Dany jest wielomian 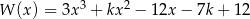 gdzie
gdzie 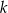 jest pewną liczbą rzeczywistą. Wiadomo, że liczba
jest pewną liczbą rzeczywistą. Wiadomo, że liczba 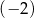 jest pierwiastkiem tego wielomianu. Liczba
jest pierwiastkiem tego wielomianu. Liczba 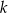 jest równa
jest równa
A) 2 B) 4 C) 6 D) 8
Dany jest wielomian 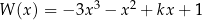 , gdzie
, gdzie 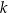 jest pewną liczbą rzeczywistą. Wiadomo, że wielomian
jest pewną liczbą rzeczywistą. Wiadomo, że wielomian 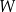 można zapisać w postaci
można zapisać w postaci 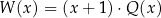 dla pewnego wielomianu
dla pewnego wielomianu 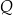 . Liczba
. Liczba 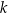 jest równa
jest równa
A) 29 B) 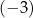 C) 0 D) 3
C) 0 D) 3
Wiadomo, że 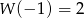 , gdy
, gdy 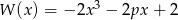 . Zatem wartość współczynnika
. Zatem wartość współczynnika 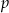 wynosi:
wynosi:
A) 6 B) -3 C) 3 D) -1
Dany jest wielomian 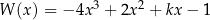 , gdzie
, gdzie 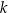 jest pewną liczbą rzeczywistą. Wiadomo, że wielomian
jest pewną liczbą rzeczywistą. Wiadomo, że wielomian 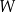 można zapisać w postaci
można zapisać w postaci 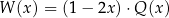 dla pewnego wielomianu
dla pewnego wielomianu 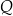 . Liczba
. Liczba 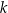 jest równa
jest równa
A) 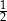 B) 2 C)
B) 2 C) 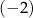 D)
D) 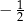
Wielomian 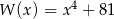 jest podzielny przez
jest podzielny przez
A) 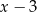 B)
B) 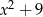 C)
C)  D)
D) 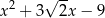
Wielomian 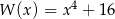 jest podzielny przez
jest podzielny przez
A) 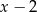 B)
B) 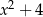 C)
C) 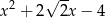 D)
D) 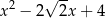
Dany jest wielomian 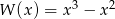 . Wartość tego wielomianu w punkcie
. Wartość tego wielomianu w punkcie 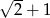 jest równa
jest równa
A) 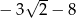 B)
B) 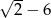 C)
C) 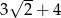 D)
D) 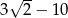
Dany jest wielomian 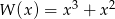 . Wartość tego wielomianu w punkcie
. Wartość tego wielomianu w punkcie 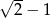 jest równa
jest równa
A) 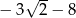 B)
B) 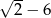 C)
C) 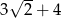 D)
D) 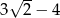
Dany jest wielomian 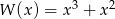 . Wartość tego wielomianu w punkcie
. Wartość tego wielomianu w punkcie 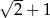 jest równa
jest równa
A) 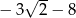 B)
B) 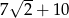 C)
C) 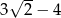 D)
D) 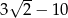
Wykres funkcji 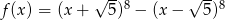 przecina oś
przecina oś 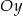 w punkcie
w punkcie
A) 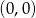 B)
B) 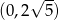 C)
C) 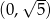 D)
D) 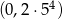
Wykres funkcji 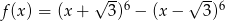 przecina oś
przecina oś 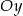 w punkcie
w punkcie
A) 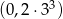 B)
B) 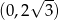 C)
C) 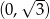 D)
D) 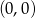
Wykres funkcji 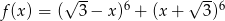 przecina oś
przecina oś 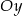 w punkcie
w punkcie
A) 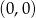 B)
B) 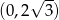 C)
C) 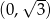 D)
D) 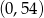
Wielomian 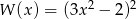 jest równy wielomianowi
jest równy wielomianowi
A) 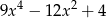 B)
B) 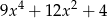 C)
C) 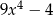 D)
D) 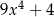
Wielomian 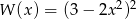 jest równy wielomianowi
jest równy wielomianowi
A) 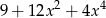 B)
B) 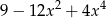 C)
C) 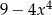 D)
D) 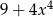
Wielomian 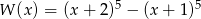 zapisano w postaci
zapisano w postaci 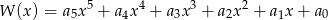 . Suma
. Suma 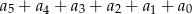 jest równa
jest równa
A) 275 B) 0 C) 1 D) 211
Wielomian 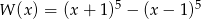 zapisano w postaci
zapisano w postaci 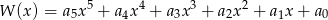 . Suma
. Suma 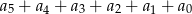 jest równa
jest równa
A) 32 B) 0 C) 1 D) 2
Wielomian 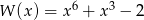 jest równy iloczynowi
jest równy iloczynowi
A) 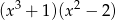 B)
B) 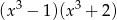 C)
C) 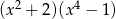 D)
D) 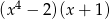
Wielomian 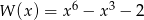 jest równy iloczynowi
jest równy iloczynowi
A) 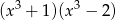 B)
B) 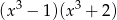 C)
C) 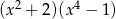 D)
D) 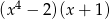
Wielomian 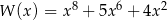 dla dowolnej liczby rzeczywistej
dla dowolnej liczby rzeczywistej  przyjmuje
przyjmuje
A) tylko wartości ujemne B) tylko wartości dodatnie
C) wartości niedodatnie D) wartości nieujemne
Wielomian 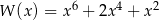 dla dowolnej liczby rzeczywistej
dla dowolnej liczby rzeczywistej  przyjmuje
przyjmuje
A) wartości niedodatnie B) wartości nieujemne
C) tylko wartości ujemne D) tylko wartości dodatnie
Wielomian 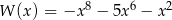 dla dowolnej liczby rzeczywistej
dla dowolnej liczby rzeczywistej  przyjmuje
przyjmuje
A) tylko wartości ujemne B) tylko wartości dodatnie
C) wartości niedodatnie D) wartości nieujemne

