Wielomian 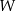 określony wzorem
określony wzorem 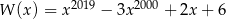
A) jest podzielny przez 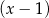 i z dzielenia przez
i z dzielenia przez 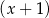 daje resztę równą 6.
daje resztę równą 6.
B) jest podzielny przez 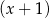 i z dzielenia przez
i z dzielenia przez 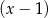 daje resztę równą 6.
daje resztę równą 6.
C) jest podzielny przez 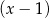 i jest podzielny przez
i jest podzielny przez 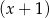 .
.
D) nie jest podzielny ani przez 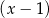 , ani przez
, ani przez 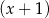 .
.
/Szkoła średnia/Zadania testowe/Funkcje/Wielomiany/Jeden wielomian
Wielomian 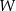 określony wzorem
określony wzorem 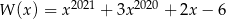
A) jest podzielny przez 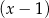 i z dzielenia przez
i z dzielenia przez 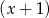 daje resztę równą
daje resztę równą 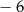 .
.
B) jest podzielny przez 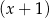 i z dzielenia przez
i z dzielenia przez 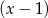 daje resztę równą
daje resztę równą 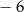 .
.
C) jest podzielny przez 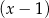 i jest podzielny przez
i jest podzielny przez 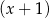 .
.
D) nie jest podzielny ani przez 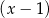 , ani przez
, ani przez 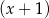 .
.
Wyraz wolny wielomianu 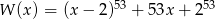 jest równy
jest równy
A) 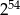 B) 0 C)
B) 0 C) 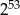 D) 53
D) 53
Wyraz wolny wielomianu 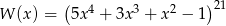 (po uporządkowaniu) jest równy
(po uporządkowaniu) jest równy
A) 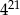 B)
B) 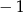 C) 1 D)
C) 1 D) 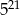
Wielomian 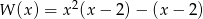 można zapisać w postaci
można zapisać w postaci
A) 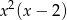 B)
B) 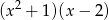 C)
C) 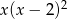 D)
D) 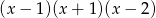
Wielomian 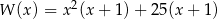 można przedstawić w postaci
można przedstawić w postaci
A) 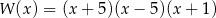 B)
B) 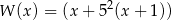
C) 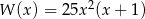 D)
D) 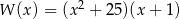
Wielomian 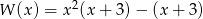 można zapisać w postaci
można zapisać w postaci
A) 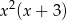 B)
B) 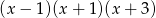 C)
C) 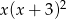 D)
D) 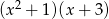
Wielomian 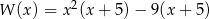 można przedstawić w postaci
można przedstawić w postaci
A) 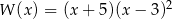 B)
B) 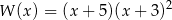
C) 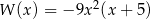 D)
D) 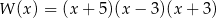
Wiadomo, że wśród pierwiastków wielomianu 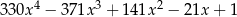 są odwrotności czterech różnych liczb pierwszych. Mediana wszystkich pierwiastków tego wielomianu jest równa
są odwrotności czterech różnych liczb pierwszych. Mediana wszystkich pierwiastków tego wielomianu jest równa
A) 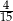 B)
B) 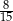 C)
C) 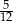 D)
D) 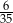
Stopień wielomianu 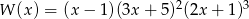 jest równy
jest równy
A) 4 B) 5 C) 6 D) 8
Stopień wielomianu 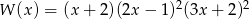 jest równy
jest równy
A) 4 B) 5 C) 6 D) 8
Stopień wielomianu 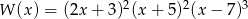 jest równy
jest równy
A) 4 B) 5 C) 6 D) 7
Wielomian 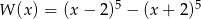 zapisano w postaci
zapisano w postaci 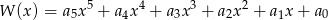 . Suma
. Suma 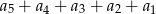 jest równa
jest równa
A) 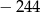 B)
B) 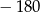 C)
C) 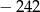 D)
D) 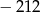
Wielomian 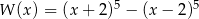 zapisano w postaci
zapisano w postaci 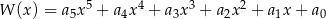 . Suma
. Suma 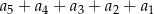 jest równa
jest równa
A) 180 B) 244 C) 242 D) 212
Wiadomo, że wielomian 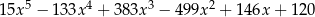 ma w zbiorze
ma w zbiorze 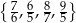 dokładnie jeden pierwiastek wymierny. Jest nim liczba
dokładnie jeden pierwiastek wymierny. Jest nim liczba
A) 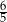 B)
B)  C)
C) 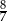 D)
D) 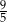
Wiadomo, że wielomian 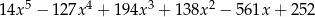 ma w zbiorze
ma w zbiorze 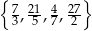 dokładnie jeden pierwiastek wymierny. Jest nim liczba
dokładnie jeden pierwiastek wymierny. Jest nim liczba
A)  B)
B) 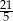 C)
C) 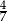 D)
D) 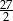
Suma współczynników wielomianu 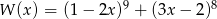 (po uporządkowaniu) jest równa
(po uporządkowaniu) jest równa
A) 0 B) 1 C) 2 D) 3
Suma współczynników wielomianu 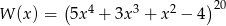 (po uporządkowaniu) jest równa
(po uporządkowaniu) jest równa
A) 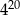 B)
B) 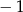 C) 1 D)
C) 1 D) 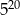
Suma wszystkich współczynników wielomianu 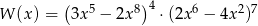 jest równa
jest równa
A) 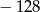 B) 216 C) 64 D)
B) 216 C) 64 D) 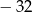
Suma wszystkich współczynników wielomianu 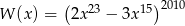 (po uporządkowaniu) wynosi
(po uporządkowaniu) wynosi
A) 0 B) 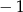 C) 1 D)
C) 1 D) 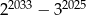
Suma współczynników wielomianu 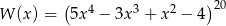 (po uporządkowaniu) jest równa
(po uporządkowaniu) jest równa
A) 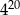 B)
B) 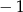 C) 1 D)
C) 1 D) 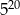
Suma wszystkich współczynników wielomianu 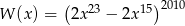 (po uporządkowaniu) wynosi
(po uporządkowaniu) wynosi
A) 0 B) 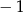 C) 1 D)
C) 1 D) 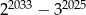
Suma wszystkich współczynników wielomianu 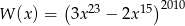 (po uporządkowaniu) wynosi
(po uporządkowaniu) wynosi
A) 0 B) 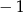 C) 1 D)
C) 1 D) 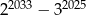
Wielomian 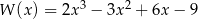 jest podzielny przez wielomian
jest podzielny przez wielomian
A) 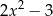 B)
B) 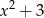 C)
C) 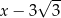 D)
D) 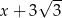
Wielomian 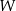 określony jest wzorem
określony jest wzorem 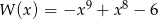 . Zatem
. Zatem 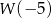 jest liczbą
jest liczbą
A) ujemną B) dodatnią C) niewymierną D) pierwszą
Wielomian 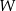 określony jest wzorem
określony jest wzorem 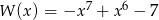 . Zatem
. Zatem 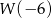 jest liczbą
jest liczbą
A) ujemną B) niewymierną C) dodatnią D) pierwszą
Wielomian 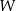 określony jest wzorem
określony jest wzorem 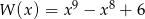 . Zatem
. Zatem 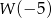 jest liczbą
jest liczbą
A) ujemną B) dodatnią C) niewymierną D) pierwszą
Po rozłożeniu wielomianu 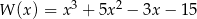 otrzymujemy
otrzymujemy
A) 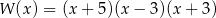 B)
B) 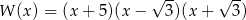
C) 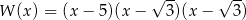 D)
D) 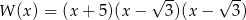
Wielomian 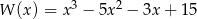 rozłożony na czynniki ma postać
rozłożony na czynniki ma postać
A) 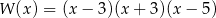 B)
B) 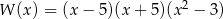
C) 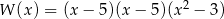 D)
D) 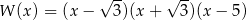
Wielomian 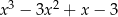 po rozłożeniu na czynniki ma postać:
po rozłożeniu na czynniki ma postać:
A) 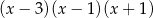 B)
B) 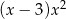
C) 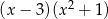 D)
D) 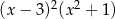
Wielomian 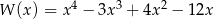 po rozłożeniu na czynniki ma postać:
po rozłożeniu na czynniki ma postać:
A) 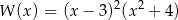 B)
B) 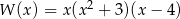
C) 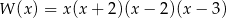 D)
D) 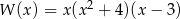
Wielomian 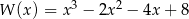 można przedstawić w postaci
można przedstawić w postaci
A) 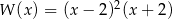 B)
B) 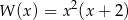
C) 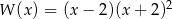 D)
D) 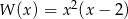
Wielomian 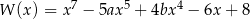 jest podzielny przez wielomian
jest podzielny przez wielomian 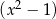 . Zatem
. Zatem
A) 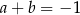 . B)
. B) 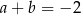 . C)
. C) 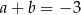 . D)
. D) 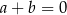 .
.
Wartość wielomianu 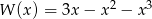 dla
dla 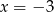 jest równa
jest równa
A) 12 B) -9 C) 9 D) -24
Wartość wielomianu 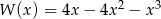 dla
dla 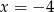 jest równa
jest równa
A) -16 B) -112 C) -144 D) 112
Wartość wielomianu 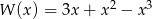 dla
dla 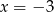 jest równa
jest równa
A) 12 B) 27 C) 9 D) -27
Dany jest wielomian 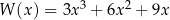 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Wielomian 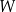 jest iloczynem wielomianów jest iloczynem wielomianów 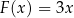 i i 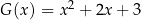 . . | P | F |
Liczba 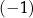 jest rozwiązaniem równania jest rozwiązaniem równania 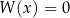 . . | P | F |
Wielomian 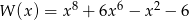 jest równy iloczynowi
jest równy iloczynowi
A) 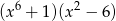 B)
B) 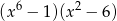 C)
C) 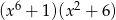 D)
D) 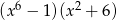
Współczynnikiem liczbowym jednomianu 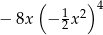 jest liczba
jest liczba
A) 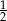 B) 4 C)
B) 4 C) 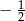 D)
D) 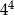
Funkcja 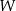 jest określona wzorem
jest określona wzorem 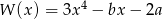 dla wszystkich liczb rzeczywistych. Równość
dla wszystkich liczb rzeczywistych. Równość 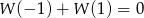 zachodzi, gdy
zachodzi, gdy
A) 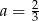 B)
B) 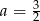 C)
C) 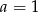 D)
D) 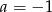
Wielomian 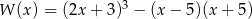 przedstawiony w postaci sumy algebraicznej przyjmuje postać:
przedstawiony w postaci sumy algebraicznej przyjmuje postać:
A) 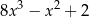 B)
B) 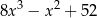
C) 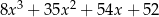 D)
D) 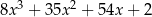
Największa wartość funkcji 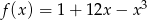
A) jest równa 17 B) jest równa 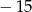 C) jest równa 4 D) nie istnieje
C) jest równa 4 D) nie istnieje
Wielomian 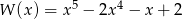
A) jest iloczynem wielomianów 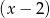 i
i 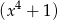
B) ma trzy miejsca zerowe
C) ma dwa miejsca zerowe
D) jest różnicą wielomianów 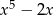 i
i 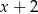
Wielomian 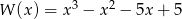
A) jest różnicą wielomianów 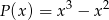 oraz
oraz 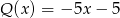
B) dla argumentu 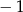 przyjmuje wartość zero
przyjmuje wartość zero
C) ma jeden pierwiastek
D) ma trzy pierwiastki
Wielomian 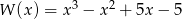
A) jest różnicą wielomianów 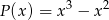 oraz
oraz 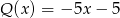
B) ma trzy pierwiastki
C) ma jeden pierwiastek
D) dla argumentu 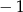 przyjmuje wartość zero
przyjmuje wartość zero
Wielomian 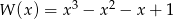
A) jest różnicą wielomianów 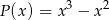 oraz
oraz 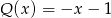
B) nie ma pierwiastków
C) ma jeden pierwiastek
D) dla argumentu 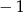 przyjmuje wartość zero
przyjmuje wartość zero

