Wykaż, że jeśli przekątna trapezu równoramiennego zawiera się w dwusiecznej jego kąta ostrego, to ramię jest równe krótszej podstawie.
/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez/Równoramienny/Udowodnij...
W trapezie równoramiennym przekątna ma długość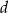 
i tworzy z dłuższą podstawą kąt o mierze 
. Wykaż, że pole tego trapezu jest równe 
.
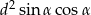Przekątna trapezu równoramiennego tworzy z dłuższą podstawą kąt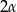 
, a z ramieniem kąt 
. Wykaż, że stosunek pól trójkątów, na które został podzielony trapez tą przekątną, jest równy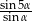 
.
Podstawy trapezu równoramiennego mają długości 
i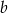 
, gdzie 
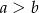. Z wierzchołka kąta rozwartego trapezu poprowadzono wysokość. Uzasadnij, że wysokość ta dzieli dłuższą podstawę na odcinki o długościach 
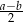i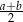 
.
