Dany jest trójkąt równoboczny 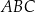 , w którym
, w którym 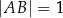 . Na boku
. Na boku 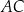 tego trójkąta wybrano taki punkt
tego trójkąta wybrano taki punkt 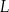 , że
, że 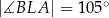 . Odcinek
. Odcinek 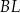 przecina wysokość
przecina wysokość 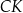 trójkąta
trójkąta 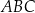 w punkcie
w punkcie 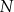 (zobacz rysunek).
(zobacz rysunek).
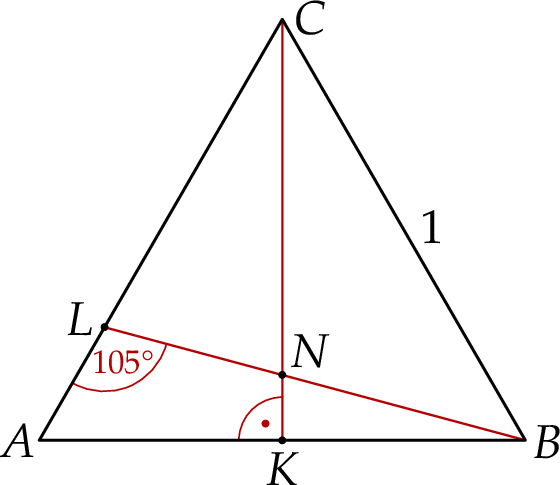
Oblicz długość odcinka 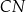 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest trójkąt równoboczny 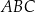 , w którym
, w którym 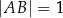 . Na boku
. Na boku 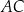 tego trójkąta wybrano taki punkt
tego trójkąta wybrano taki punkt 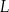 , że
, że 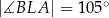 . Odcinek
. Odcinek 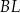 przecina wysokość
przecina wysokość 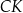 trójkąta
trójkąta 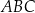 w punkcie
w punkcie 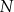 (zobacz rysunek).
(zobacz rysunek).

Oblicz długość odcinka 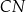 .
.
Wysokość trójkąta równobocznego jest o 3 cm krótsza od długości jego boku. Oblicz promień okręgu opisanego na tym trójkącie.
Oblicz długość boku kwadratu wpisanego w trójkąt równoboczny o boku  .
.
Na boku 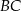 trójkąta równobocznego
trójkąta równobocznego 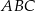 wybrano taki punkt
wybrano taki punkt 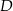 , że pole trójkąta
, że pole trójkąta 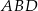 jest równe
jest równe 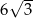 i jest dwa razy większe od pola trójkąta
i jest dwa razy większe od pola trójkąta 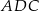 (zobacz rysunek).
(zobacz rysunek).
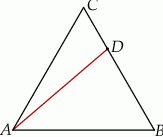
Oblicz długość odcinka 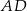 .
.
Trójkąt równoboczny 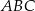 ma pole równe
ma pole równe 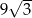 . Prosta równoległa do boku
. Prosta równoległa do boku 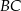 przecina boki
przecina boki 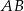 i
i 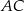 – odpowiednio – w punktach
– odpowiednio – w punktach 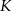 i
i 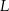 . Trójkąty
. Trójkąty 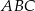 i
i 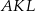 są podobne, a stosunek długości boków tych trójkątów jest równy
są podobne, a stosunek długości boków tych trójkątów jest równy  . Oblicz długość boku trójkąta
. Oblicz długość boku trójkąta 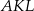 .
.
Trójkąt równoboczny 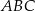 ma pole równe
ma pole równe 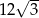 . Prosta równoległa do boku
. Prosta równoległa do boku 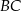 przecina boki
przecina boki 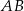 i
i 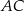 – odpowiednio – w punktach
– odpowiednio – w punktach 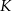 i
i 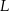 . Stosunek obwodów trójkątów
. Stosunek obwodów trójkątów 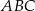 i
i 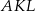 jest równy
jest równy 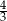 . Oblicz długość boku trójkąta
. Oblicz długość boku trójkąta 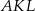 .
.
Oblicz długość boku trójkąta równobocznego, wiedząc, że bok ten jest o 2 cm dłuższy od wysokości tego trójkąta.
Przez środek okręgu wpisanego w trójkąt równoboczny 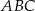 poprowadzono prostą równoległą do boku
poprowadzono prostą równoległą do boku 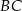 i przecinającą bok
i przecinającą bok 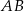 w punkcie
w punkcie 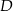 . Oblicz iloraz
. Oblicz iloraz 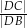 .
.
Dwa trójkąty równoboczne mają wspólny środek i boki równoległe. Pole jednego jest 2 razy większe od pola drugiego, a boki mniejszego trójkąta mają długość 1. Jaka jest odległość między równoległymi bokami?
Trójkąty 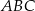 i
i 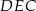 są przystającymi trójkątami równobocznymi o boku długości 6. Odcinki
są przystającymi trójkątami równobocznymi o boku długości 6. Odcinki 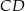 i
i 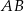 są prostopadłe, a odcinek
są prostopadłe, a odcinek 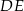 przecina odcinki
przecina odcinki 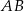 i
i 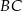 w punktach
w punktach 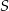 i
i 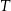 odpowiednio (zobacz rysunek). Oblicz długość odcinka
odpowiednio (zobacz rysunek). Oblicz długość odcinka  .
.
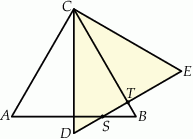
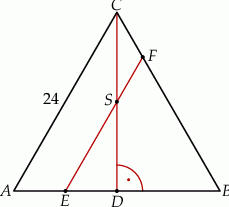
Dany jest trójkąt równoboczny 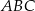 o boku długości 24. Punkt
o boku długości 24. Punkt 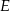 leży na boku
leży na boku 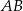 , a punkt
, a punkt 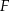 – na boku
– na boku 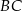 tego trójkąta. Odcinek
tego trójkąta. Odcinek 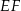 jest równoległy do boku
jest równoległy do boku 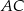 i przechodzi przez środek
i przechodzi przez środek 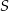 wysokości
wysokości 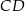 trójkąta
trójkąta 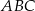 (zobacz rysunek).
(zobacz rysunek).
Oblicz długość odcinka 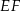 .
.
