Zadania.info Największy internetowy zbiór zadań z matematyki

/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Dowolny/Czworokątny/Romb w podstawie

Wyszukiwanie zadań

Podstawą ostrosłupa jest romb, którego przekątne mają długości 12 i 16. Spodek wysokości ostrosłupa pokrywa się z punktem przecięcia przekątnych rombu w podstawie, a pole powierzchni bocznej jest równe 104. Oblicz objętość ostrosłupa.

Podstawą ostrosłupa 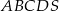ABCDS jest romb 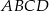ABCD , w którym 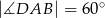∘ |∡DAB | = 60 . Krawędź 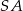SA jest wysokością ostrosłupa oraz jej długość jest równa długości krawędzi podstawy. Oblicz sinus kąta nachylenia ściany 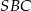SBC do płaszczyzny podstawy.

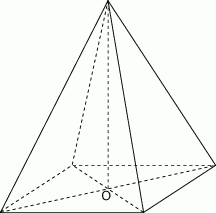
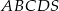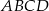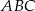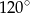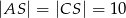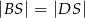Podstawą ostrosłupa ABCDS jest romb ABCD o boku długości 4. Kąt ABC rombu ma miarę 120∘ oraz |AS | = |CS | = 10 i |BS | = |DS | . Oblicz sinus kąta nachylenia krawędzi 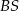BS do płaszczyzny podstawy ostrosłupa.

Podstawą ostrosłupa jest romb o boku długości 18 cm. Każda ze ścian bocznych tworzy z płaszczyzną podstawy kąt 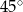45∘ . Pole powierzchni bocznej ostrosłupa jest równe 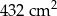43 2 cm 2 . Oblicz jego objętość.

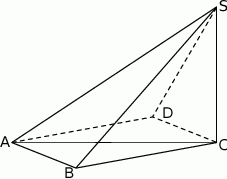
Podstawą ostrosłupa 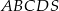ABCDS jest romb o boku długości 6. Krawędź boczna 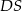DS ma długość 8 i jest jednocześnie wysokością tego ostrosłupa. Długości pozostałych trzech krawędzi bocznych są równe (zobacz rysunek).

PIC

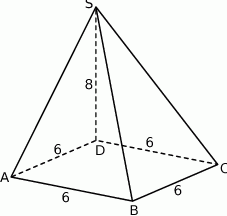
Oblicz objętość tego ostrosłupa.

Podstawą ostrosłupa jest romb, którego pole wynosi 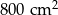2 800 cm , a kąt ostry rombu ma miarę 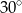30∘ . Wysokość ostrosłupa jest równa 24 cm, a spodek tej wysokości jest środkiem okręgu wpisanego w podstawę. Oblicz:

  • promień tego okręgu,
  • pole powierzchni bocznej ostrosłupa.

Podstawą ostrosłupa 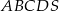ABCDS jest romb 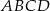ABCD . Krawędź 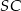SC jest prostopadła do płaszczyzny podstawy, krawędź 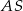AS ma długość 4 i jest nachylona do płaszczyzny podstawy pod kątem 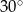30∘ . Krawędź 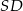SD ma długość 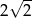2√ 2- . Oblicz objętość tego ostrosłupa.

PIC

Podstawą ostrosłupa jest romb. Wysokość ostrosłupa ma długość 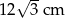√ -- 12 3 cm , a spodek 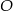O tej wysokości jest punktem przecięcia przekątnych. Każda ze ścian bocznych ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze 60∘ .

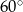  • Zaznacz na rysunku kąt nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa oraz poprowadź odcinek 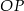OP , którego długość jest równa odległości punktu 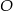O od ściany bocznej.
  • Oblicz odległość punktu 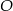O od ściany bocznej.
PIC