Dany jest trójmian kwadratowy 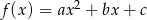 .
.
- Dla
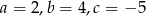 wyznacz największą i najmniejszą wartość tego trójmianu w przedziale
wyznacz największą i najmniejszą wartość tego trójmianu w przedziale 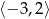 .
. - Wyznacz wzór trójmianu w postaci iloczynowej, jeśli wiadomo, że ma on miejsca zerowe
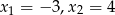 , a do jego wykresu należy punkt
, a do jego wykresu należy punkt 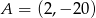 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest trójmian kwadratowy 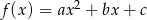 .
.
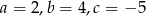 wyznacz największą i najmniejszą wartość tego trójmianu w przedziale
wyznacz największą i najmniejszą wartość tego trójmianu w przedziale 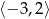 .
. 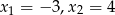 , a do jego wykresu należy punkt
, a do jego wykresu należy punkt 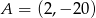 .
.Funkcja kwadratowa 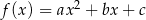 ma dwa miejsca zerowe
ma dwa miejsca zerowe 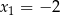 i
i 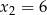 . Wykres funkcji
. Wykres funkcji 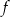 przechodzi przez punkt
przechodzi przez punkt 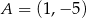 . Oblicz najmniejszą wartość funkcji
. Oblicz najmniejszą wartość funkcji 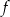 .
.
Funkcja kwadratowa 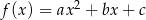 ma dwa miejsca zerowe
ma dwa miejsca zerowe 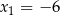 i
i 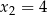 . Wykres funkcji
. Wykres funkcji 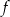 przechodzi przez punkt
przechodzi przez punkt 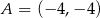 . Oblicz najmniejszą wartość funkcji
. Oblicz najmniejszą wartość funkcji 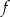 .
.
Parabola, która jest wykresem funkcji kwadratowej 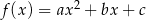 , przechodzi przez punkt
, przechodzi przez punkt 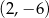 oraz
oraz 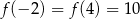 . Oblicz odległość wierzchołka tej paraboli od początku układu współrzędnych.
. Oblicz odległość wierzchołka tej paraboli od początku układu współrzędnych.
Funkcja kwadratowa 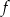 jest określona dla wszystkich liczb rzeczywistych
jest określona dla wszystkich liczb rzeczywistych  wzorem
wzorem 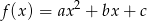 . Największa wartość funkcji
. Największa wartość funkcji 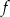 jest równa 6 oraz
jest równa 6 oraz 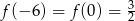 . Oblicz wartość współczynnika
. Oblicz wartość współczynnika  .
.
Funkcja kwadratowa 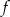 jest określona dla wszystkich liczb rzeczywistych
jest określona dla wszystkich liczb rzeczywistych  wzorem
wzorem 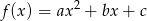 . Najmniejsza wartość funkcji
. Najmniejsza wartość funkcji 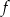 jest równa
jest równa 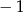 oraz
oraz 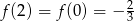 . Oblicz wartość współczynnika
. Oblicz wartość współczynnika  .
.
