Obwód trójkąta prostokątnego wynosi 60 cm, a tangens jednego z kątów ostrych jest równy 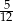 . Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego na przeciwprostokątną.
. Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego na przeciwprostokątną.
/Szkoła średnia/Geometria/Planimetria/Trójkąt
Obwód trójkąta prostokątnego wynosi 72 cm, a tangens jednego z kątów ostrych jest równy 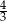 . Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego na przeciwprostokątną.
. Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego na przeciwprostokątną.
Na bokach 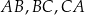 trójkąta równobocznego
trójkąta równobocznego 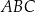 wybrano kolejno punkty
wybrano kolejno punkty 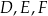 tak, że
tak, że 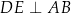 ,
, 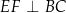 i
i 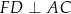 .
.

Wykaż, że trójkąt 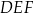 jest trójkątem równobocznym o polu trzy razy mniejszym od pola trójkąta
jest trójkątem równobocznym o polu trzy razy mniejszym od pola trójkąta 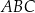 .
.
W trójkącie 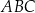 dane są długości dwóch boków
dane są długości dwóch boków 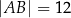 ,
, 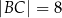 oraz miara kąta
oraz miara kąta 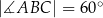 . Oblicz długość środkowej tego trójkąta poprowadzonej z wierzchołka A.
. Oblicz długość środkowej tego trójkąta poprowadzonej z wierzchołka A.
Dany jest trójkąt prostokątny o polu 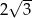 i kącie ostrym
i kącie ostrym 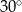 . Oblicz długości przyprostokątnych tego trójkąta.
. Oblicz długości przyprostokątnych tego trójkąta.
Dany jest trójkąt prostokątny o polu 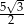 i kącie ostrym
i kącie ostrym  . Oblicz długości przyprostokątnych tego trójkąta.
. Oblicz długości przyprostokątnych tego trójkąta.
Dany jest trójkąt prostokątny o polu 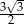 i kącie ostrym
i kącie ostrym 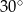 . Oblicz długości przyprostokątnych tego trójkąta.
. Oblicz długości przyprostokątnych tego trójkąta.
Dany jest trójkąt równoboczny 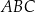 , w którym
, w którym 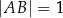 . Na boku
. Na boku 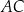 tego trójkąta wybrano taki punkt
tego trójkąta wybrano taki punkt 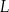 , że
, że 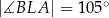 . Odcinek
. Odcinek 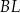 przecina wysokość
przecina wysokość 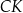 trójkąta
trójkąta 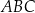 w punkcie
w punkcie 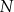 (zobacz rysunek).
(zobacz rysunek).
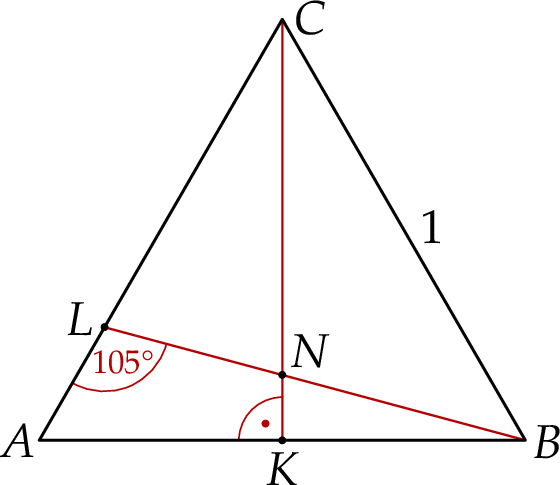
Oblicz długość odcinka 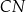 .
.
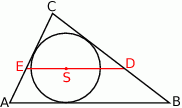
Przez środek 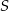 okręgu wpisanego w trójkąt
okręgu wpisanego w trójkąt 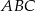 poprowadzono prostą równoległą do boku
poprowadzono prostą równoległą do boku 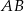 , która przecina boki
, która przecina boki 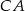 i
i 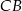 odpowiednio w punktach
odpowiednio w punktach 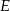 i
i 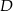 .
.
Wykaż, że 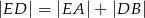 .
.
Dany jest trójkąt o wymiarach 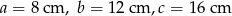 . Oblicz obwód trójkąta podobnego w skali 5.
. Oblicz obwód trójkąta podobnego w skali 5.
Dany jest trójkąt o wymiarach 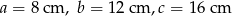 . Oblicz obwód trójkąta podobnego w skali
. Oblicz obwód trójkąta podobnego w skali 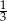 .
.
W trójkącie równobocznym 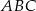 połączono środki wysokości otrzymując trójkąt
połączono środki wysokości otrzymując trójkąt 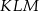 . Oblicz stosunek pól trójkątów
. Oblicz stosunek pól trójkątów 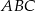 i
i 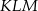 .
.
Liczby 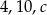 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
Liczby 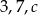 są długościami boków trójkąta równoramiennego. Oblicz długość boku
są długościami boków trójkąta równoramiennego. Oblicz długość boku  .
.
Liczby 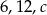 są długościami boków trójkąta równoramiennego. Oblicz długość boku
są długościami boków trójkąta równoramiennego. Oblicz długość boku  .
.
Dany jest trójkąt prostokątny 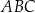 , w którym
, w którym 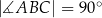 oraz
oraz 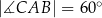 . Punkty
. Punkty 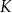 i
i 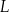 leżą na bokach – odpowiednio –
leżą na bokach – odpowiednio – 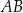 i
i 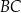 tak, że
tak, że 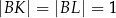 (zobacz rysunek). Odcinek
(zobacz rysunek). Odcinek 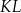 przecina wysokość
przecina wysokość 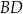 tego trójkąta w punkcie
tego trójkąta w punkcie 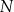 , a ponadto
, a ponadto 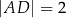 .
.
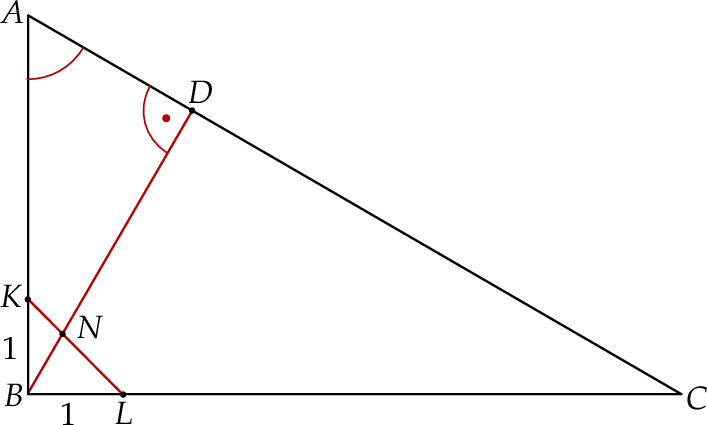
Wykaż, że 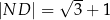 .
.
Wykaż, że wysokość 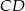 trójkąta prostokątnego
trójkąta prostokątnego 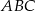 poprowadzona z wierzchołka
poprowadzona z wierzchołka 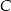 kąta prostego dzieli przeciwprostokątną na odcinki
kąta prostego dzieli przeciwprostokątną na odcinki 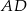 i
i 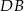 , których stosunek długości jest równy stosunkowi kwadratów długości przyprostokątnych odpowiednio
, których stosunek długości jest równy stosunkowi kwadratów długości przyprostokątnych odpowiednio 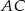 i
i 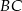 tego trójkąta.
tego trójkąta.
Na okręgu o promieniu 1 opisano trójkąt prostokątny, którego przyprostokątne mają długości  i
i 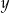 .
.
- Wyznacz
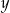 jako funkcję
jako funkcję  i określ dziedzinę tej funkcji.
i określ dziedzinę tej funkcji. - Sporządź wykres tej funkcji.
Wysokość trójkąta równobocznego jest o 3 cm krótsza od długości jego boku. Oblicz promień okręgu opisanego na tym trójkącie.
Na zewnątrz trójkąta prostokątnego 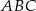 , w którym
, w którym 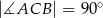 oraz
oraz 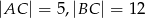 zbudowano kwadrat
zbudowano kwadrat 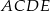 .
.
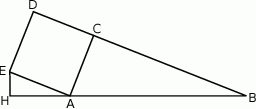
Punkt 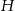 leży na prostej
leży na prostej 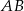 i kąt
i kąt 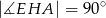 . Oblicz pole trójkąta
. Oblicz pole trójkąta 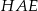 .
.
Sinus kąta 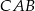 trójkąta równoramiennego
trójkąta równoramiennego 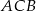 jest równy
jest równy 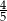 . Pole kwadratu
. Pole kwadratu 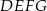 , wpisanego w ten trójkąt (zobacz rysunek), jest równe 4. Oblicz pole trójkąta
, wpisanego w ten trójkąt (zobacz rysunek), jest równe 4. Oblicz pole trójkąta 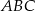 .
.
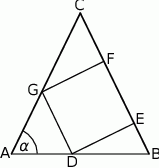
Dany jest trójkąt prostokątny 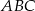 , w którym
, w którym 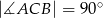 i
i 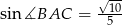 . Niech
. Niech 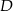 oznacza punkt wspólny wysokości poprowadzonej z wierzchołka
oznacza punkt wspólny wysokości poprowadzonej z wierzchołka 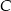 kąta prostego i przeciwprostokątnej
kąta prostego i przeciwprostokątnej 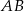 tego trójkąta. Wykaż, że
tego trójkąta. Wykaż, że 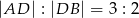 .
.
W trójkącie ostrokątnym 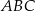 bok
bok 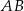 ma długość
ma długość  , długość boku
, długość boku 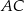 jest równa
jest równa 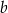 oraz
oraz 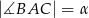 . Dwusieczna kąta
. Dwusieczna kąta 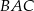 przecina bok
przecina bok 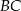 trójkąta w punkcie
trójkąta w punkcie 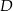 i odcinek
i odcinek 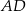 ma długość
ma długość 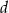 . Wykaż, że
. Wykaż, że
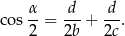
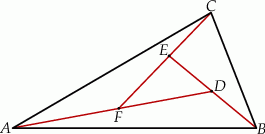
W trójkącie 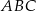 poprowadzono odcinki
poprowadzono odcinki 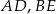 i
i 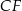 w ten sposób, że punkty
w ten sposób, że punkty 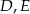 i
i 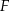 są środkami odpowiednio odcinków
są środkami odpowiednio odcinków 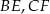 i
i 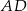 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 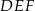 jest siedem razy mniejsze od pola trójkąta
jest siedem razy mniejsze od pola trójkąta 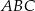 .
.
W trójkącie 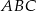 dane są
dane są 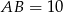 ,
, 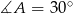 i
i 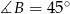 . Oblicz długości pozostałych boków tego trójkąta i promień okręgu opisanego na tym trójkącie.
. Oblicz długości pozostałych boków tego trójkąta i promień okręgu opisanego na tym trójkącie.
Oblicz cosinus najmniejszego kąta  trójkąta o bokach 2 cm, 4 cm, 5 cm.
trójkąta o bokach 2 cm, 4 cm, 5 cm.
Dany jest trójkąt 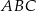 o bokach długości 6, 7 oraz 8. Oblicz cosinus najmniejszego kąta tego trójkąta.
o bokach długości 6, 7 oraz 8. Oblicz cosinus najmniejszego kąta tego trójkąta.
Dany jest trójkąt 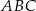 o bokach długości 6, 7 oraz 8. Oblicz cosinus największego kąta tego trójkąta.
o bokach długości 6, 7 oraz 8. Oblicz cosinus największego kąta tego trójkąta.

