Na bokach trójkąta 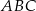 zbudowano kwadraty
zbudowano kwadraty 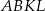 ,
, 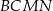 i
i 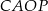 (zobacz rysunek).
(zobacz rysunek).
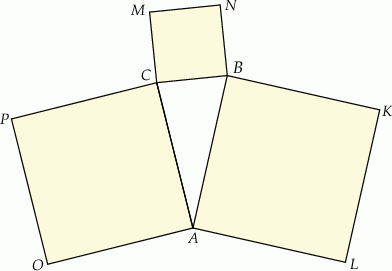
Kąty 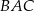 i
i 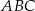 są ostre oraz suma ich tangensów jest równa
są ostre oraz suma ich tangensów jest równa  . Wykaż, że jeżeli pole kwadratu
. Wykaż, że jeżeli pole kwadratu 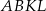 jest pięć razy większe od pola trójkąta
jest pięć razy większe od pola trójkąta 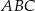 , to suma pól kwadratów
, to suma pól kwadratów 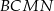 i
i 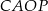 też jest pięć razy większa od pola trójkąta
też jest pięć razy większa od pola trójkąta 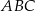 .
.

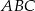 środkowa
środkowa 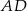 jest prostopadła do boku
jest prostopadła do boku 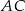 oraz
oraz 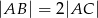 . Oblicz miarę kąta
. Oblicz miarę kąta 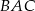 .
. 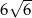 . Ramię jest o 30% krótsze od podstawy. Oblicz obwód tego trójkąta.
. Ramię jest o 30% krótsze od podstawy. Oblicz obwód tego trójkąta. 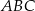 dane są kąt
dane są kąt 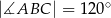 ,
, 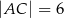 i
i 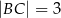 . Dwusieczna kąta
. Dwusieczna kąta 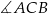 przecina bok
przecina bok 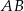 w punkcie
w punkcie 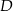 . Oblicz długość odcinka
. Oblicz długość odcinka 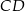 .
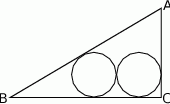
. 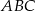 o przyprostokątnych długości
o przyprostokątnych długości 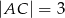 i
i 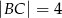 wpisano dwa przystające okręgi w ten sposób, że są one wzajemnie styczne oraz jeden z nich jest styczny do boków
wpisano dwa przystające okręgi w ten sposób, że są one wzajemnie styczne oraz jeden z nich jest styczny do boków 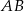 i
i 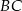 , a drugi do boków
, a drugi do boków 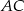 i
i  .
. 
 takie, że trójkąt o bokach
takie, że trójkąt o bokach 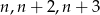 jest rozwartokątny.
jest rozwartokątny. 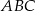 , w którym
, w którym 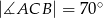 połączono środek okręgu wpisanego
połączono środek okręgu wpisanego 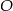 z wierzchołkami
z wierzchołkami 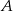 i
i 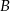 . Oblicz miarę kąta
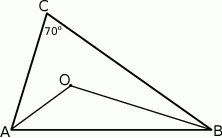
. Oblicz miarę kąta 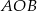 .
. 
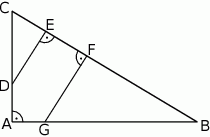
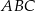 odcinek
odcinek 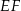 o końcach należących do boków odpowiednio
o końcach należących do boków odpowiednio 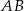 i
i 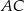 przecina środkową
przecina środkową 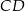 w punkcie
w punkcie 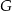 , oraz odcinek
, oraz odcinek 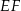 jest równoległy do odcinka
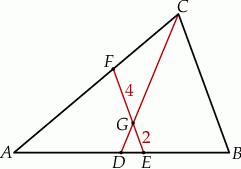
jest równoległy do odcinka 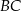 (patrz rysunek). Oblicz długość odcinka
(patrz rysunek). Oblicz długość odcinka 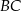 wiedząc, że
wiedząc, że 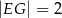 i
i 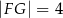 .
. 
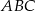 , w którym przyprostokątna
, w którym przyprostokątna 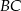 ma długość 6. Punkt
ma długość 6. Punkt 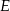 jest środkiem przeciwprostokątnej
jest środkiem przeciwprostokątnej 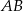 , spodek
, spodek 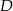 wysokości
wysokości 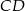 leży między punktami
leży między punktami 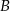 i
i 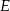 , a odległość między punktami
, a odległość między punktami 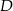 i
i 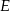 jest równa 7 (zobacz rysunek).
jest równa 7 (zobacz rysunek). 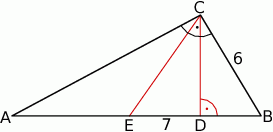
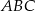 .
. 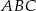 . Na przyprostokątnych
. Na przyprostokątnych 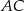 i
i 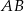 tego trójkąta obrano odpowiednio punkty
tego trójkąta obrano odpowiednio punkty 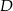 i
i 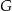 . Na przeciwprostokątnej
. Na przeciwprostokątnej 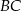 wyznaczono punkty
wyznaczono punkty 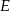 i
i 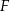 takie, że
takie, że 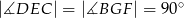 (zobacz rysunek). Wykaż, że trójkąt
(zobacz rysunek). Wykaż, że trójkąt 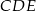 jest podobny do trójkąta
jest podobny do trójkąta 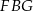 .
. 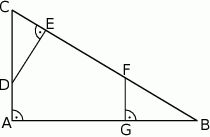
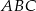 . Na przyprostokątnych
. Na przyprostokątnych 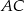 i
i 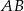 tego trójkąta obrano odpowiednio punkty
tego trójkąta obrano odpowiednio punkty 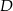 i
i 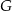 . Na przeciwprostokątnej
. Na przeciwprostokątnej 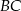 wyznaczono punkty
wyznaczono punkty 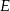 i
i 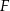 takie, że
takie, że 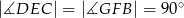 (zobacz rysunek). Wykaż, że trójkąt
(zobacz rysunek). Wykaż, że trójkąt 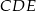 jest podobny do trójkąta
jest podobny do trójkąta  .
. 
 . Na przyprostokątnych
. Na przyprostokątnych  i
i 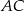 tego trójkąta obrano odpowiednio punkty
tego trójkąta obrano odpowiednio punkty 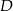 i
i 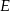 takie, że
takie, że 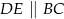 . Na przeciwprostokątnej
. Na przeciwprostokątnej 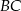 wyznaczono punkt
wyznaczono punkt 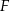 taki, że
taki, że 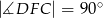 (zobacz rysunek). Wykaż, że trójkąt
(zobacz rysunek). Wykaż, że trójkąt 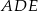 jest podobny do trójkąta
jest podobny do trójkąta 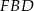 .
. 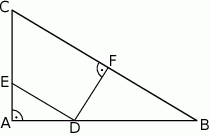
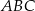 obrano na boku
obrano na boku 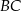 taki punkt
taki punkt 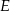 , że
, że 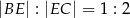 . Oblicz tangens kąta
. Oblicz tangens kąta 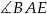 .
. 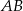 trójkąta równobocznego
trójkąta równobocznego 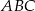 wybrano punkt
wybrano punkt 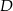 taki, że
taki, że 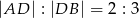 . Oblicz tangens kąta
. Oblicz tangens kąta 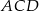 .
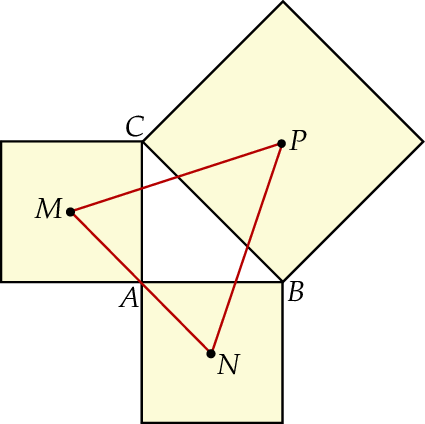
.  zbudowano kwadraty tak, że bok każdego kwadratu jest jednocześnie bokiem trójkąta. Środki symetrii tych kwadratów połączono odcinkami i otrzymano trójkąt
zbudowano kwadraty tak, że bok każdego kwadratu jest jednocześnie bokiem trójkąta. Środki symetrii tych kwadratów połączono odcinkami i otrzymano trójkąt 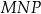 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 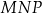 jest równe
jest równe 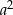 .
. 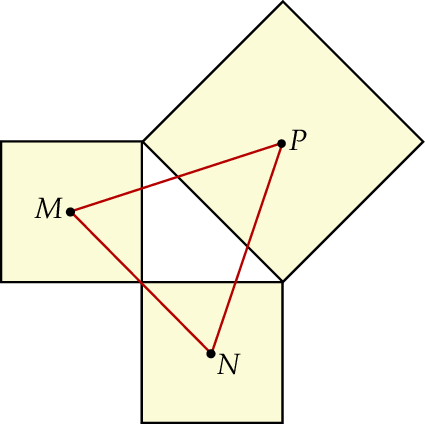
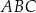 zbudowano kwadraty tak, że bok każdego kwadratu jest jednocześnie bokiem trójkąta. Środki symetrii tych kwadratów połączono odcinkami i otrzymano trójkąt
zbudowano kwadraty tak, że bok każdego kwadratu jest jednocześnie bokiem trójkąta. Środki symetrii tych kwadratów połączono odcinkami i otrzymano trójkąt 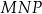 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 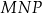 jest dwa razy większe od pola trójkąta
jest dwa razy większe od pola trójkąta 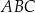 .
. 
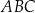 o przeciwprostokątnej
o przeciwprostokątnej 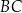 punkt
punkt 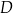 jest środkiem ramienia
jest środkiem ramienia 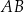 . Odcinek
. Odcinek 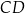 ma długość 5 (zobacz rysunek).
ma długość 5 (zobacz rysunek). 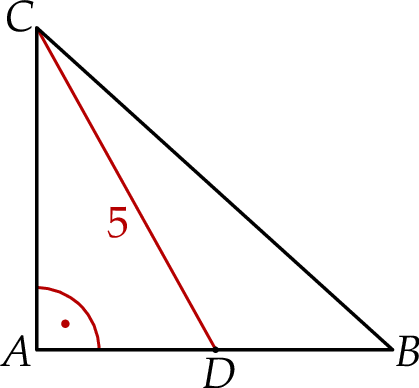
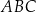 .
. 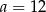 cm i wysokości
cm i wysokości 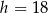 cm. W trójkąt ten wpisano prostokąt w ten sposób, że dwa wierzchołki prostokąta leżą na podstawie, a po jednym na każdym ramieniu trójkąta, przy czym przekątne prostokąta są równoległe do ramion trójkąta. Oblicz długości boków prostokąta.
cm. W trójkąt ten wpisano prostokąt w ten sposób, że dwa wierzchołki prostokąta leżą na podstawie, a po jednym na każdym ramieniu trójkąta, przy czym przekątne prostokąta są równoległe do ramion trójkąta. Oblicz długości boków prostokąta.  i
i 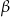 są takie, że
są takie, że 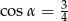 i
i 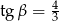 .
. 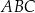 ma miarę mniejszą niż
ma miarę mniejszą niż 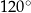 . Na bokach tego trójkąta zbudowano trójkąty równoboczne
. Na bokach tego trójkąta zbudowano trójkąty równoboczne 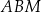 ,
, 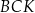 i
i 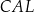 (zobacz rysunek).
(zobacz rysunek). 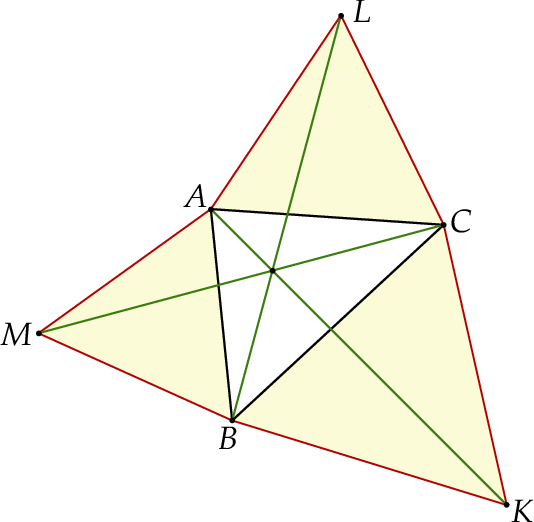
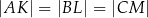 .
. 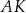 ,
, 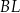 i
i 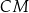 przecinają się w jednym punkcie (jest to tzw. punkt
przecinają się w jednym punkcie (jest to tzw. punkt 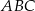 boki
boki 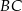 i
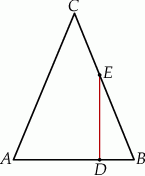
i 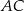 są równej długości. Prosta
są równej długości. Prosta 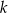 jest prostopadła do podstawy
jest prostopadła do podstawy 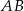 tego trójkąta i przecina boki
tego trójkąta i przecina boki 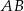 oraz
oraz 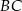 w punktach – odpowiednio –
w punktach – odpowiednio – 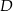 i
i 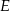 . Pole czworokąta
. Pole czworokąta 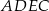 jest 17 razy większe od pola trójkąta
jest 17 razy większe od pola trójkąta 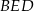 . Oblicz
. Oblicz 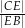 .
. 
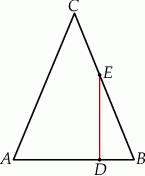
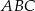 boki
boki 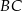 i
i 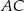 są równej długości. Prosta
są równej długości. Prosta 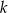 jest prostopadła do podstawy
jest prostopadła do podstawy 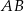 tego trójkąta i przecina boki
tego trójkąta i przecina boki 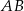 oraz
oraz 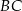 w punktach – odpowiednio –
w punktach – odpowiednio – 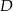 i
i 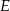 . Oblicz stosunek pola czworokąta
. Oblicz stosunek pola czworokąta 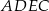 do pola trójkąta
do pola trójkąta 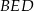 jeżeli
jeżeli 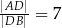 .
. 
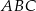 długości boków
długości boków 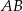 i
i 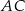 są odpowiednio równe 4 i 6. Punkt
są odpowiednio równe 4 i 6. Punkt 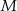 jest środkiem odcinka
jest środkiem odcinka 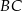 , a długość środkowej
, a długość środkowej 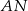 trójkąta
trójkąta 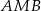 jest równa 3. Oblicz długość boku
jest równa 3. Oblicz długość boku 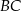 .
. 