Promień okręgu opisanego na trójkącie 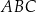 jest równy 17. Najdłuższym bokiem tego trójkąta jest bok
jest równy 17. Najdłuższym bokiem tego trójkąta jest bok 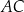 , a długości dwóch pozostałych boków są równe
, a długości dwóch pozostałych boków są równe 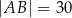 oraz
oraz 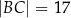 . Oblicz miarę kąta
. Oblicz miarę kąta 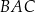 oraz długość boku
oraz długość boku 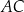 tego trójkąta.
tego trójkąta.
/Szkoła średnia/Geometria/Planimetria/Trójkąt
Jeden z boków trójkąta ma długość  , zaś kąty trójkąta przyległe do tego boku mają miary
, zaś kąty trójkąta przyległe do tego boku mają miary  i
i 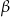 . Znajdź promień okręgu wpisanego w ten trójkąt.
. Znajdź promień okręgu wpisanego w ten trójkąt.
W trójkącie 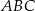 dane są długości boków
dane są długości boków 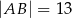 i
i 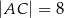 oraz
oraz 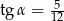 , gdzie
, gdzie 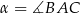 . Oblicz pole trójkąta
. Oblicz pole trójkąta 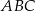 .
.
W trójkącie  długość boku
długość boku  stanowi
stanowi 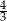 długości boku
długości boku 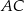 , a kąt
, a kąt 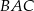 ma miarę
ma miarę 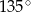 . Oblicz cosinus kąta
. Oblicz cosinus kąta 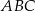 .
.
Środkowa 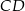 trójkąta
trójkąta 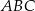 jest równa bokowi
jest równa bokowi 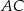 . Wyznacz kąty trójkąta
. Wyznacz kąty trójkąta 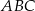 wiedząc, że
wiedząc, że 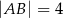 i
i 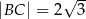 .
.
Na bokach 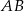 i
i 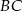 trójkąta
trójkąta 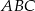 wybrano punkty
wybrano punkty 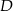 i
i 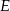 w ten sposób, że odcinek
w ten sposób, że odcinek 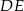 jest styczny do okręgu wpisanego w trójkąt
jest styczny do okręgu wpisanego w trójkąt 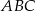 oraz trójkąt
oraz trójkąt 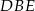 jest równoboczny. Obwód trójkąta
jest równoboczny. Obwód trójkąta 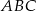 jest równy 20, a długość boku
jest równy 20, a długość boku 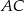 jest równa 7. Oblicz pole trójkąta
jest równa 7. Oblicz pole trójkąta 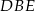 .
.
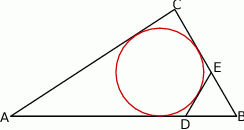
Dany jest trójkąt 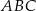 , w którym
, w którym 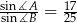 . Na boku
. Na boku 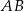 leży punkt
leży punkt 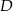 taki, że
taki, że 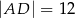 ,
, 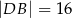 oraz
oraz 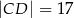 . Oblicz długość promienia okręgu opisanego na trójkącie
. Oblicz długość promienia okręgu opisanego na trójkącie 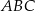 .
.
W trójkącie kąt między bokami o długościach 8 i 6 jest równy 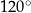 . Jaką długość ma trzeci bok trójkąta?
. Jaką długość ma trzeci bok trójkąta?
W trójkącie kąt między bokami o długościach 6 i 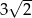 jest równy
jest równy 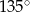 . Jaką długość ma trzeci bok trójkąta?
. Jaką długość ma trzeci bok trójkąta?
Dany jest trójkąt równoboczny 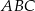 . Na bokach
. Na bokach 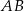 i
i 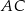 wybrano punkty – odpowiednio –
wybrano punkty – odpowiednio –  i
i  takie, że
takie, że 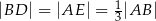 . Odcinki
. Odcinki 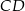 i
i 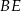 przecinają się w punkcie
przecinają się w punkcie 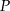 (zobacz rysunek).
(zobacz rysunek).
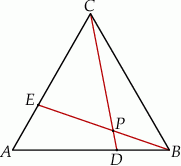
Wykaż, że pole trójkąta 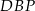 jest 21 razy mniejsze od pola trójkąta
jest 21 razy mniejsze od pola trójkąta 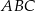 .
.
Dany jest trójkąt równoboczny 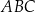 . Na bokach
. Na bokach 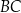 i
i 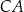 wybrano punkty – odpowiednio –
wybrano punkty – odpowiednio – 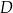 i
i 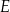 takie, że
takie, że 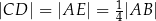 . Odcinki
. Odcinki 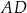 i
i 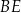 przecinają się w punkcie
przecinają się w punkcie 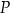 (zobacz rysunek).
(zobacz rysunek).
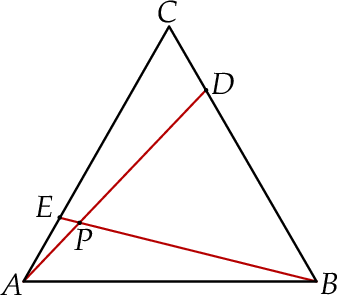
Wykaż, że pole trójkąta 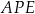 jest 52 razy mniejsze od pola trójkąta
jest 52 razy mniejsze od pola trójkąta 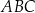 .
.
Wykaż, że jeżeli  i
i 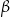 są kątami trójkąta oraz
są kątami trójkąta oraz 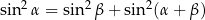 to trójkąt ten jest prostokątny.
to trójkąt ten jest prostokątny.
Punkty 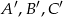 są środkami boków trójkąta
są środkami boków trójkąta 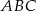 . Pole trójkąta
. Pole trójkąta 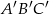 jest równe 4. Oblicz pole trójkąta
jest równe 4. Oblicz pole trójkąta 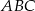 .
.
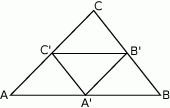
Oblicz długości boków trójkąta prostokątnego, którego obwód wynosi 70, a pole 210.
Oblicz długości boków trójkąta prostokątnego, którego obwód wynosi 40, a pole 60.
Środkowa 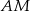 trójkąta
trójkąta 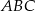 ma długość równą połowie długości boku
ma długość równą połowie długości boku 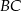 . Miara kąta między tą środkową a wysokością
. Miara kąta między tą środkową a wysokością 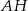 jest równa
jest równa 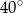 . Wyznacz miary kątów trójkąta
. Wyznacz miary kątów trójkąta 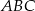 .
.
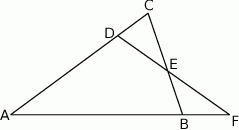
Dany jest trójkąt 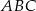 , w którym
, w którym 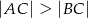 . Na bokach
. Na bokach 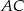 i
i 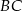 tego trójkąta obrano odpowiednio takie punkty
tego trójkąta obrano odpowiednio takie punkty 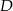 i
i 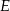 , że zachodzi równość
, że zachodzi równość 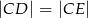 . Proste
. Proste 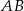 i
i 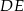 przecinają się w punkcie
przecinają się w punkcie 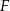 (zobacz rysunek). Wykaż, że
(zobacz rysunek). Wykaż, że 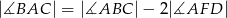 .
.
Dany jest trójkąt 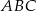 , w którym
, w którym 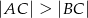 . Na bokach
. Na bokach 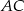 i
i 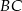 tego trójkąta obrano odpowiednio takie punkty
tego trójkąta obrano odpowiednio takie punkty 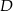 i
i 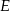 , że zachodzi równość
, że zachodzi równość 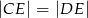 . Proste
. Proste 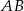 i
i 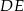 przecinają się w punkcie
przecinają się w punkcie 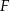 (zobacz rysunek). Wykaż, że
(zobacz rysunek). Wykaż, że 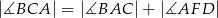 .
.
Wykaż, że jeżeli pole koła opisanego na trójkącie prostokątnym jest 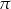 razy większe od pola trójkąta, to trójkąt ten jest równoramienny.
razy większe od pola trójkąta, to trójkąt ten jest równoramienny.
W trójkącie równoramiennym 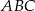 , w którym
, w którym 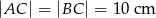 , wysokość poprowadzona z wierzchołka
, wysokość poprowadzona z wierzchołka 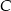 jest równa 5 cm. Oblicz miary kątów tego trójkąta. Odpowiedź podaj w stopniach.
jest równa 5 cm. Oblicz miary kątów tego trójkąta. Odpowiedź podaj w stopniach.
W trójkącie 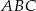 proste zawierające dwusieczne kątów poprowadzonych z wierzchołków
proste zawierające dwusieczne kątów poprowadzonych z wierzchołków 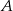 i
i 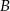 przecinają się pod kątem
przecinają się pod kątem 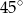 . Wiedząc, że
. Wiedząc, że 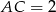 i
i 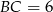 , oblicz
, oblicz
- długość boku
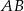 trójkąta
trójkąta 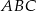 ;
; - długość środkowej trójkąta
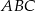 poprowadzonej z wierzchołka
poprowadzonej z wierzchołka 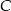 .
.
Wykaż, że jeśli 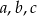 są długościami boków trójkąta ostrokątnego takimi, że
są długościami boków trójkąta ostrokątnego takimi, że 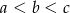 oraz
oraz 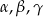 są miarami kątów tego trójkąta leżącymi odpowiednio na przeciwko boków
są miarami kątów tego trójkąta leżącymi odpowiednio na przeciwko boków 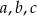 , to
, to 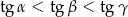 .
.
W trójkącie 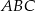 połączono środki boków i otrzymano trójkąt
połączono środki boków i otrzymano trójkąt 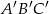 . Uzasadnij, że trójkąty
. Uzasadnij, że trójkąty 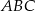 i
i 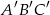 są podobne.
są podobne.
Punkty 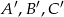 są środkami odpowiednio boków
są środkami odpowiednio boków 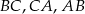 trójkąta
trójkąta 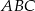 . Uzasadnij, że trójkąt
. Uzasadnij, że trójkąt 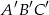 jest przystający do trójkąta
jest przystający do trójkąta 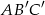 .
.
W trójkącie ostrokątnym 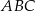 wysokości
wysokości 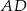 i
i 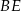 przecinają się w punkcie
przecinają się w punkcie 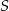 . Wiadomo, że
. Wiadomo, że 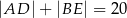 ,
, 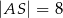 ,
, 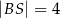 . Wyznacz długości odcinków
. Wyznacz długości odcinków 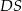 i
i 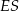 .
.

