Trójkąt  jest ostrokątny oraz
jest ostrokątny oraz 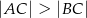 . Dwusieczna
. Dwusieczna 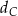 kąta
kąta 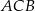 przecina bok
przecina bok 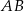 w punkcie
w punkcie 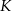 . Punkt
. Punkt 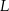 jest obrazem punktu
jest obrazem punktu 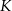 w symetrii osiowej względem dwusiecznej
w symetrii osiowej względem dwusiecznej 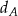 kąta
kąta 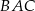 , punkt
, punkt 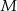 jest obrazem punktu
jest obrazem punktu 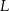 w symetrii osiowej względem dwusiecznej
w symetrii osiowej względem dwusiecznej 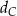 kąta
kąta 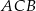 , a punkt
, a punkt 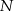 jest obrazem punktu
jest obrazem punktu 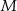 w symetrii osiowej względem dwusiecznej
w symetrii osiowej względem dwusiecznej 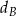 kąta
kąta 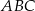 (zobacz rysunek).
(zobacz rysunek).
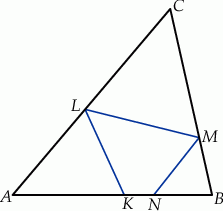
Udowodnij, że na czworokącie 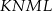 można opisać okrąg.
można opisać okrąg.

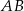 ,
, 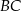 i
i 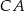 trójkąta
trójkąta 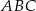 wybrano odpowiednio punkty
wybrano odpowiednio punkty 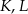 i
i 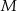 w ten sposób, że
w ten sposób, że 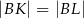 i
i 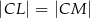 . Okrąg opisany na trójkącie
. Okrąg opisany na trójkącie 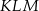 przecina bok
przecina bok 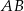 tego trójkąta w punkcie
tego trójkąta w punkcie 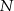 takim, że
takim, że 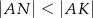 (zobacz rysunek).
(zobacz rysunek). 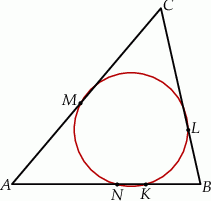
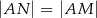 .
. 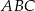 bok
bok 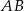 ma długość 8, a bok
ma długość 8, a bok 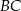 ma długość 10. Dwusieczna kąta
ma długość 10. Dwusieczna kąta 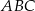 przecina bok
przecina bok 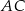 w punkcie
w punkcie 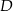 takim, że
takim, że 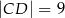 (zobacz rysunek).
(zobacz rysunek). 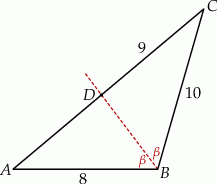
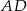 .
. 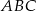 bok
bok 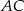 ma długość
ma długość 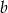 ,
, 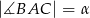 oraz
oraz 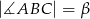 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 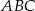 jest równe
jest równe 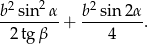
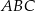 i
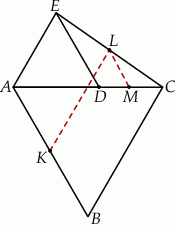
i 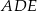 są równoboczne (zobacz rysunek). Punkty
są równoboczne (zobacz rysunek). Punkty 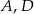 i
i 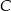 leżą na jednej prostej. Punkty
leżą na jednej prostej. Punkty 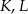 i
i 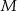 są środkami odcinków
są środkami odcinków 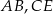 i
i 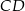 . Wykaż, że
. Wykaż, że 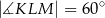 .
. 
 , w którym
, w którym 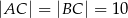 ,
, 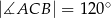 . Na boku
. Na boku 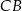 obrano punkt
obrano punkt 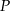 dzielący ten bok w stosunku 3:2 (licząc od punktu
dzielący ten bok w stosunku 3:2 (licząc od punktu 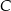 ). Oblicz sinus kąta
). Oblicz sinus kąta 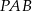 .
. 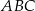 :
: 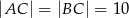 , a miara kąta
, a miara kąta 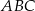 jest równa
jest równa 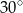 . Na boku
. Na boku 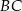 wybrano punkt
wybrano punkt 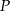 , taki, że
, taki, że 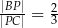 . Oblicz sinus kąta
. Oblicz sinus kąta  (zobacz rysunek).
(zobacz rysunek). 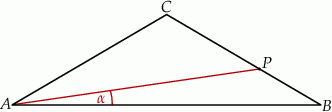
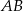 trójkąta równoramiennego
trójkąta równoramiennego 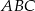 ma długość 8 oraz
ma długość 8 oraz 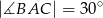 . Oblicz długość środkowej
. Oblicz długość środkowej 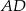 tego trójkąta.
tego trójkąta. 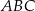 i
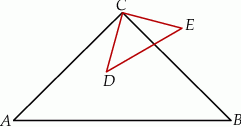
i 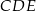 są położone tak, jak na poniższym rysunku (w obu trójkątach kąt przy wierzchołku
są położone tak, jak na poniższym rysunku (w obu trójkątach kąt przy wierzchołku 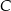 jest prosty). Wykaż, że
jest prosty). Wykaż, że 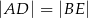 .
. 
 i
i  są położone tak, jak na poniższym rysunku.
są położone tak, jak na poniższym rysunku. 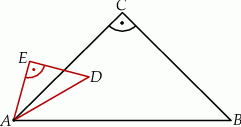
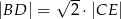 .
. 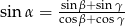 to trójkąt ten jest prostokątny.
to trójkąt ten jest prostokątny. 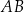 trójkąta
trójkąta 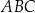 wybrano punkt
wybrano punkt 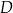 w ten sposób, że
w ten sposób, że 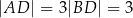 . Bok
. Bok 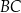 tego trójkąta ma długość 2. Oblicz stosunek długości odcinków
tego trójkąta ma długość 2. Oblicz stosunek długości odcinków 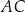 i
i 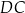 .
. 
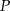 wewnątrz trójkąta równobocznego od boków tego trójkąta jest stała, tzn. nie zależy od wyboru tego punktu.
wewnątrz trójkąta równobocznego od boków tego trójkąta jest stała, tzn. nie zależy od wyboru tego punktu. 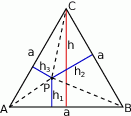
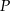 z wierzchołkami trójkąta i zapisujemy równość pól
z wierzchołkami trójkąta i zapisujemy równość pól 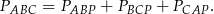
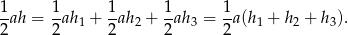
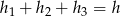 , a więc suma ta nie zależy od wyboru punktu
, a więc suma ta nie zależy od wyboru punktu 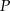 .
.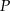 wewnątrz czworościanu foremnego od jego ścian jest stała, to znaczy nie zależy od wyboru punktu
wewnątrz czworościanu foremnego od jego ścian jest stała, to znaczy nie zależy od wyboru punktu 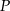 .
. 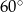 , promień okręgu wpisanego w ten trójkąt ma długość 1. Oblicz długości boków trójkąta.
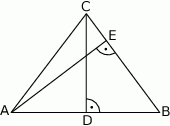
, promień okręgu wpisanego w ten trójkąt ma długość 1. Oblicz długości boków trójkąta. 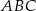 (patrz rysunek,
(patrz rysunek, 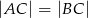 ), w którym wysokość
), w którym wysokość 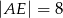 , a długość odcinka
, a długość odcinka 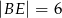 .
. 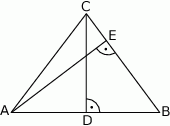
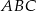 (patrz rysunek,
(patrz rysunek, 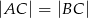 ), w którym wysokość
), w którym wysokość 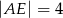 , a długość odcinka
, a długość odcinka 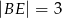 .
. 
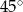 oblicz
oblicz 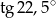 .
. 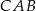 trójkąta prostokątnego
trójkąta prostokątnego 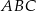 ma miarę
ma miarę 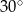 . Odcinek
. Odcinek 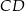 jest wysokością tego trójkąta opuszczoną na przeciwprostokątną
jest wysokością tego trójkąta opuszczoną na przeciwprostokątną 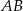 . Oblicz stosunek pól trójkątów
. Oblicz stosunek pól trójkątów 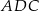 i
i 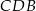 .
. 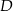 leży na boku
leży na boku 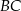 trójkąta
trójkąta 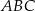 oraz
oraz 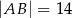 ,
, 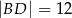 ,
, 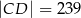 i
i 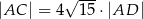 . Oblicz pole trójkąta
. Oblicz pole trójkąta 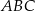 .
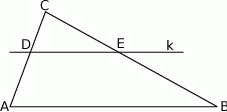
. 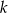 równoległa do boku
równoległa do boku 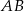 trójkąta
trójkąta 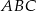 przecina boki
przecina boki 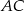 oraz
oraz 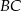 odpowiednio w punktach
odpowiednio w punktach 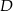 i
i 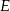 (zobacz rysunek). Wiadomo, że pole trójkąta
(zobacz rysunek). Wiadomo, że pole trójkąta 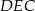 wynosi
wynosi 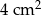 , zaś pole trapezu
, zaś pole trapezu 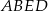 jest równe
jest równe 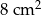 . Wykaż, że
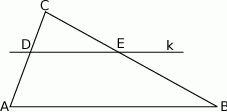
. Wykaż, że 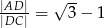 .
. 
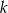 równoległa do boku
równoległa do boku 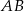 trójkąta
trójkąta 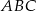 przecina boki
przecina boki 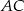 oraz
oraz 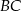 odpowiednio w punktach
odpowiednio w punktach 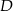 i
i 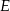 (zobacz rysunek). Wiadomo, że pole trójkąta
(zobacz rysunek). Wiadomo, że pole trójkąta 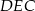 wynosi
wynosi 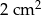 , zaś pole trapezu
, zaś pole trapezu 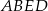 jest równe
jest równe 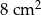 . Wykaż, że
. Wykaż, że 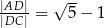 .
.