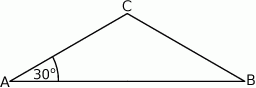
Kąt przy podstawie trójkąta równoramiennego 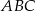 ma miarę
ma miarę 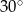 . Uzasadnij, że pole trójkąta jest trzy razy mniejsze od pola trójkąta równobocznego o boku równym podstawie trójkąta
. Uzasadnij, że pole trójkąta jest trzy razy mniejsze od pola trójkąta równobocznego o boku równym podstawie trójkąta 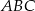 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Kąt przy podstawie trójkąta równoramiennego 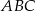 ma miarę
ma miarę 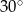 . Uzasadnij, że pole trójkąta jest trzy razy mniejsze od pola trójkąta równobocznego o boku równym podstawie trójkąta
. Uzasadnij, że pole trójkąta jest trzy razy mniejsze od pola trójkąta równobocznego o boku równym podstawie trójkąta 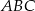 .
.

Z wierzchołka kąta prostego trójkąta prostokątnego 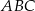 poprowadzono wysokość
poprowadzono wysokość 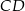 , która podzieliła przeciwprostokątną
, która podzieliła przeciwprostokątną 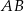 na odcinki o długościach 32 cm i 18 cm (zobacz rysunek).
na odcinki o długościach 32 cm i 18 cm (zobacz rysunek).
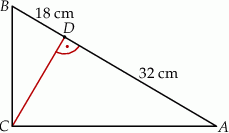
Oblicz pole trójkąta 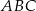 .
.
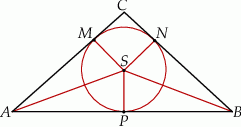
W trójkąt równoramienny 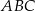 (
(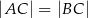 ) wpisano okrąg o środku
) wpisano okrąg o środku 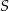 . Punkty wspólne okręgu i trójkąta oznaczono literami
. Punkty wspólne okręgu i trójkąta oznaczono literami 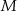 ,
, 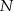 i
i 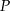 . Uzasadnij, że trójkąty
. Uzasadnij, że trójkąty 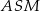 i
i 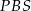 są przystające.
są przystające.
Ze środka ciężkości trójkąta równobocznego o boku  , wykreślono okrąg o promieniu
, wykreślono okrąg o promieniu 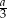 . Oblicz pole części koła nie należącego do trójkąta.
. Oblicz pole części koła nie należącego do trójkąta.
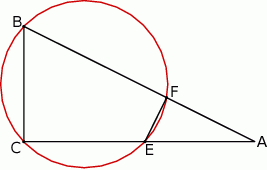
W okrąg wpisany jest trójkąt 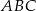 , przy czym
, przy czym 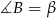 i
i 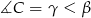 . Oblicz miarę kąta między prostą
. Oblicz miarę kąta między prostą 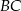 i styczną do okręgu w punkcie
i styczną do okręgu w punkcie 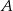 .
.
Dane są długości boków  i
i 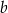 trójkąta. Znajdź długość trzeciego boku, jeżeli kąt leżący naprzeciw tego boku jest dwa razy większy od kąta leżącego naprzeciw boku
trójkąta. Znajdź długość trzeciego boku, jeżeli kąt leżący naprzeciw tego boku jest dwa razy większy od kąta leżącego naprzeciw boku 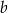 .
.
Trójkąt prostokątny 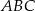 ma boki długości 3, 4, 5. Oblicz promień okręgu stycznego do przeciwprostokątnej i prostych będących przedłużeniami przyprostokątnych.
ma boki długości 3, 4, 5. Oblicz promień okręgu stycznego do przeciwprostokątnej i prostych będących przedłużeniami przyprostokątnych.
Na wysokości 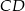 trójkąta
trójkąta 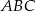 wybrano punkt
wybrano punkt 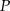 taki, że
taki, że 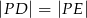 , gdzie
, gdzie 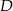 i
i 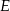 są rzutami tego punktu odpowiednio na boki
są rzutami tego punktu odpowiednio na boki 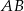 i
i 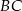 . Wiedząc, że
. Wiedząc, że 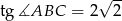 oblicz iloraz
oblicz iloraz  .
.
W okrąg o promieniu 4 wpisano trójkąt 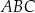 . Długość boku
. Długość boku 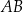 jest równa 6. Bok
jest równa 6. Bok 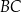 ma długość
ma długość 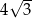 i jest najdłuższym bokiem tego trójkąta. Oblicz długość boku
i jest najdłuższym bokiem tego trójkąta. Oblicz długość boku 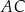 trójkąta
trójkąta 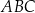 .
.
Na podstawie twierdzenia Pitagorasa można udowodnić bardziej ogólną własność niż ta, o której mówi samo to twierdzenie.
Rozważmy trójkąt prostokątny 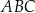 o kącie prostym przy wierzchołku
o kącie prostym przy wierzchołku 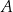 . Niech każdy z boków tego trójkąta:
. Niech każdy z boków tego trójkąta: 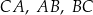 będzie podstawą trójkątów podobnych, odpowiednio:
będzie podstawą trójkątów podobnych, odpowiednio: 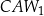 ,
, 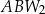 ,
, 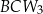 . Trójkąty te mają odpowiadające sobie kąty o równych miarach, odpowiednio przy wierzchołkach:
. Trójkąty te mają odpowiadające sobie kąty o równych miarach, odpowiednio przy wierzchołkach: 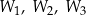 .
.

Pola trójkątów: 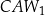 ,
, 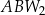 ,
, 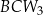 oznaczymy odpowiednio jako
oznaczymy odpowiednio jako 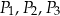 . Udowodnij, że
. Udowodnij, że
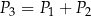
W trójkącie równoramiennym 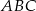 (
(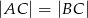 ) miara kąta
) miara kąta 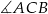 jest równa
jest równa 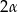 . Promień okręgu wpisanego w ten trójkąt ma długość
. Promień okręgu wpisanego w ten trójkąt ma długość  . Oblicz długości boków trójkąta
. Oblicz długości boków trójkąta 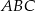 .
.
Wierzchołki 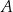 i
i 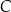 trójkąta
trójkąta 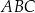 leżą na okręgu o promieniu
leżą na okręgu o promieniu  . Środek
. Środek 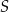 tego okręgu leży na boku
tego okręgu leży na boku 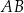 tego trójkąta (zobacz rysunek poniżej). Długości boków
tego trójkąta (zobacz rysunek poniżej). Długości boków 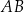 i
i 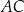 są równe odpowiednio
są równe odpowiednio 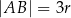 oraz
oraz 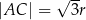 .
.
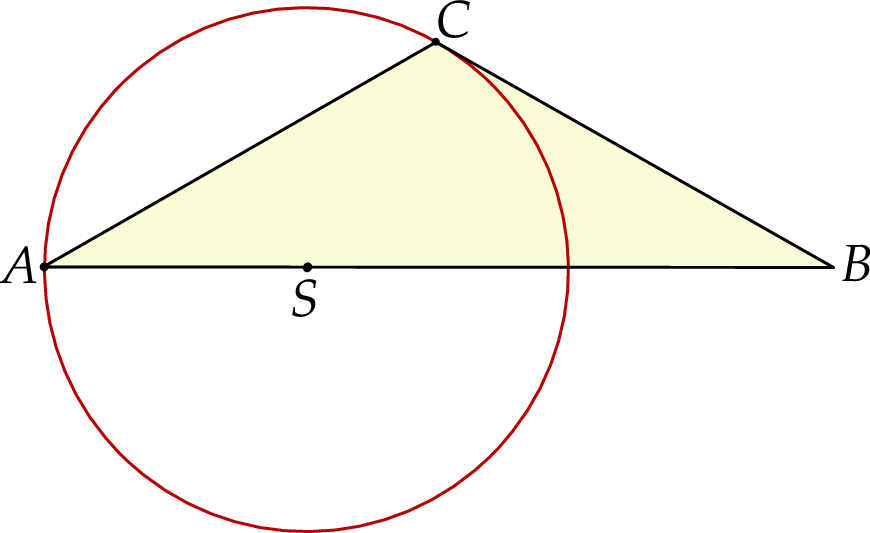
Oblicz miary wszystkich kątów wewnętrznych trójkąta 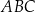 .
.
Udowodnij, że jeżeli w trójkącie dwa kąty nie są równe, to naprzeciw większego z nich leży dłuższy bok.
Wykaż, że pole trójkąta o bokach 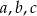 i promieniu
i promieniu 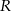 okręgu opisanego na nim jest równe
okręgu opisanego na nim jest równe 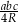 .
.
Wykaż, że pole trójkąta 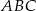 jest równe
jest równe 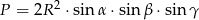 , gdzie
, gdzie 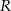 jest promieniem okręgu opisanego na tym trójkącie, a
jest promieniem okręgu opisanego na tym trójkącie, a 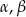 i
i 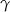 są miarami kątów wewnętrznych tego trójkąta.
są miarami kątów wewnętrznych tego trójkąta.
Długości boków trójkąta są w stosunku 2 : 3 : 4. Oblicz cosinus największego kąta tego trójkąta.
W trójkącie 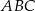 bok
bok 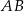 jest 3 razy dłuższy od boku
jest 3 razy dłuższy od boku 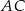 , a długość boku
, a długość boku 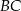 stanowi
stanowi  długości boku
długości boku 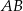 . Oblicz cosinus najmniejszego kąta trójkąta
. Oblicz cosinus najmniejszego kąta trójkąta 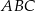 .
.
W trójkącie 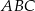 bok
bok 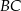 jest 3 razy krótszy od boku
jest 3 razy krótszy od boku 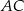 , a długość boku
, a długość boku 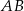 stanowi
stanowi  długości boku
długości boku 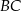 . Oblicz cosinus największego kąta trójkąta
. Oblicz cosinus największego kąta trójkąta 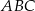 .
.
Dany jest trójkąt 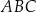 o bokach długości:
o bokach długości: 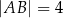 ,
, 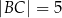 ,
, 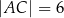 . Oblicz sinus najmniejszego kąta wewnętrznego trójkąta
. Oblicz sinus najmniejszego kąta wewnętrznego trójkąta 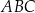 .
.
Dany jest trójkąt 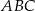 . Punkt
. Punkt 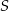 jest środkiem boku
jest środkiem boku 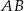 tego trójkąta (zobacz rysunek). Wykaż, że odległości punktów
tego trójkąta (zobacz rysunek). Wykaż, że odległości punktów 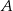 i
i 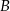 od prostej
od prostej 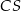 są równe.
są równe.
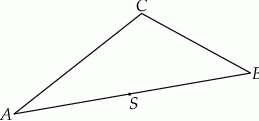
Na boku 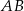 trójkąta
trójkąta 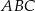 wybrano punkt
wybrano punkt 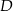 w ten sposób, że odległości punktów
w ten sposób, że odległości punktów 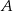 i
i 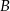 od prostej
od prostej 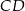 są równe (zobacz rysunek). Wykaż, że trójkąty
są równe (zobacz rysunek). Wykaż, że trójkąty 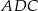 i
i 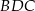 mają równe pola.
mają równe pola.
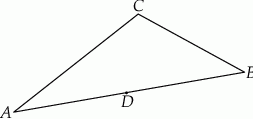
Na trójkącie równobocznym opisano drugi trójkąt równoboczny tak, że wierzchołki pierwszego trójkąta leżą na bokach drugiego. Boki obydwu trójkątów tworzą kąty 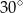 . Jakim procentem pola małego trójkąta jest pole dużego trójkąta?
. Jakim procentem pola małego trójkąta jest pole dużego trójkąta?
W trójkącie równoramiennym 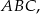 w którym
w którym 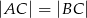 i
i 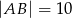 , poprowadzono dwusieczną kąta
, poprowadzono dwusieczną kąta 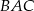 przecinająca bok
przecinająca bok 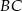 w punkcie
w punkcie 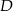 . Wówczas okazało się, że
. Wówczas okazało się, że 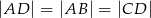 .
.
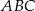 .
. 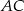 .
. 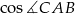 .
.Okrąg przechodzący przez końce przyprostokątnej 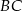 trójkąta prostokątnego
trójkąta prostokątnego 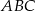 przecina drugą przyprostokątną
przecina drugą przyprostokątną 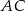 oraz przeciwprostokątną
oraz przeciwprostokątną 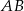 tego trójkąta odpowiednio w punktach
tego trójkąta odpowiednio w punktach 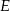 i
i 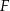 . Wykaż, że promień okręgu opisanego na trójkącie
. Wykaż, że promień okręgu opisanego na trójkącie 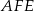 jest równy
jest równy 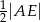 .
.