W trójkącie równoramiennym podstawa ma długość 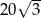 . Pole trójkąta jest równe
. Pole trójkąta jest równe 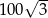 . Oblicz obwód tego trójkąta i miarę kąta przy podstawie.
. Oblicz obwód tego trójkąta i miarę kąta przy podstawie.
/Szkoła średnia/Geometria/Planimetria/Trójkąt
Oblicz sumę długości boków i pole trójkąta prostokątnego, w którym jedna z przyprostokątnych jest równa 10 cm, a druga jest o 2 cm krótsza od przeciwprostokątnej.
Oblicz długość boku kwadratu wpisanego w trójkąt równoboczny o boku  .
.
Miary dwóch kątów trójkąta wynoszą 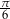 i
i 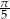 . Oblicz miarę trzeciego kąta. Odpowiedź podaj w stopniach.
. Oblicz miarę trzeciego kąta. Odpowiedź podaj w stopniach.
Na środkowej 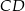 trójkąta
trójkąta 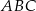 wybrano punkt
wybrano punkt 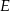 . Wykaż, że trójkąty
. Wykaż, że trójkąty 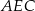 i
i 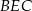 mają równe pola.
mają równe pola.
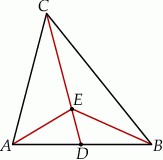
Odcinki 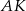 i
i 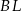 są wysokościami trójkąta ostrokątnego
są wysokościami trójkąta ostrokątnego 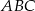 , a punkt
, a punkt 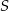 jest punktem ich przecięcia. Uzasadnij, że:
jest punktem ich przecięcia. Uzasadnij, że:
- na czworokącie
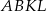 można opisać okrąg;
można opisać okrąg; - okręgi opisane na trójkątach
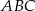 i
i 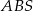 mają promienie równej długości.
mają promienie równej długości.
Obwód trójkąta 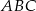 jest równy 8. Oblicz obwód trójkąta
jest równy 8. Oblicz obwód trójkąta 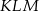 o wierzchołkach będących środkami środkowych trójkąta
o wierzchołkach będących środkami środkowych trójkąta 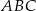 .
.
Promień okręgu opisanego na trójkącie prostokątnym ma długość 3 dm, a długość promienia okręgu wpisanego w trójkąt prostokątny wynosi 1 dm. Oblicz obwód tego trójkąta.
Oblicz sumę tangensów kątów ostrych trójkąta prostokątnego wiedząc że stosunek pola tego trójkąta do pola kwadratu, którego bokiem jest przeciwprostokątna danego trójkąta wynosi  .
.
Stosunek pola trójkąta prostokątnego do pola kwadratu, zbudowanego na przeciwprostokątnej tego trójkąta jest równy  . Oblicz sumę tangensów kątów ostrych tego trójkąta.
. Oblicz sumę tangensów kątów ostrych tego trójkąta.
Pole trójkąta 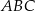 jest równe
jest równe 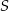 , a długości jego boków
, a długości jego boków 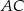 i
i 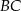 są odpowiednio równe
są odpowiednio równe 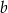 i
i  . Na bokach
. Na bokach 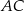 i
i 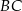 zbudowano kwadraty o środkach odpowiednio
zbudowano kwadraty o środkach odpowiednio 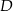 i
i 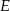 .
.
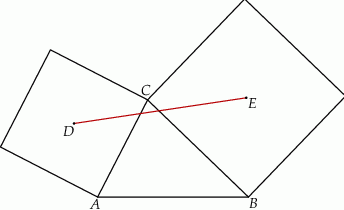
Wykaż, że
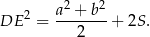
Przekątne trapezu 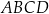 są prostopadłe i przecinają się w punkcie
są prostopadłe i przecinają się w punkcie 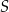 . Podstawa
. Podstawa 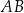 tego trapezu ma długość 15, a odcinki
tego trapezu ma długość 15, a odcinki 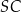 i
i 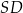 mają odpowiednio długości 6 i 8. Oblicz pole trójkąta
mają odpowiednio długości 6 i 8. Oblicz pole trójkąta 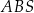 .
.
Okrąg wpisany w trójkąt równoboczny 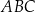 jest jednocześnie okręgiem opisanym na trójkącie równobocznym
jest jednocześnie okręgiem opisanym na trójkącie równobocznym 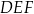 . O ile procent pole trójkąta
. O ile procent pole trójkąta 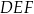 jest mniejsze od pola trójkąta
jest mniejsze od pola trójkąta 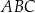 ?
?
Wykaż, że jeżeli w trójkącie 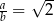 to
to 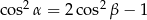 .
.
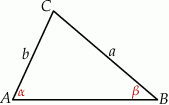
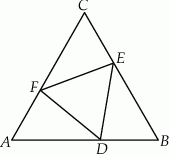
W trójkąt równoboczny 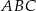 wpisano trójkąt
wpisano trójkąt 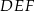 (patrz rysunek), tak że
(patrz rysunek), tak że 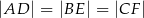 . Udowodnij, że trójkąt
. Udowodnij, że trójkąt 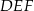 jest równoboczny.
jest równoboczny.
W trójkącie równoramiennym wysokość opuszczona na podstawę jest równa 36, a promień okręgu wpisanego w ten trójkąt jest równy 10. Oblicz długości boków tego trójkąta i promień okręgu opisanego na tym trójkącie.
Dany jest trójkąt równoramienny 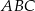 , w którym
, w którym 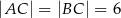 , a punkt
, a punkt 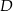 jest środkiem podstawy
jest środkiem podstawy 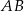 . Okrąg o środku
. Okrąg o środku 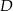 jest styczny do prostej
jest styczny do prostej 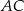 w punkcie
w punkcie 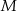 . Punkt
. Punkt 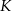 leży na boku
leży na boku 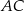 , punkt
, punkt 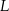 leży na boku
leży na boku 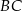 , odcinek
, odcinek 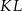 jest styczny do rozważanego okręgu oraz
jest styczny do rozważanego okręgu oraz 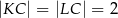 (zobacz rysunek).
(zobacz rysunek).
Wykaż, że 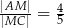 .
.
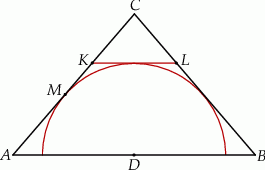
Dany jest trójkąt równoramienny 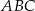 , w którym
, w którym 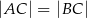 , a punkt
, a punkt 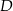 jest środkiem podstawy
jest środkiem podstawy 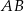 . Okrąg o środku
. Okrąg o środku 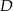 jest styczny do prostej
jest styczny do prostej 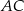 . Punkt
. Punkt 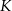 leży na boku
leży na boku 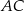 , punkt
, punkt 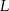 leży na boku
leży na boku 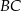 , odcinek
, odcinek 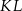 jest styczny do rozważanego okręgu oraz
jest styczny do rozważanego okręgu oraz 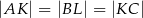 (zobacz rysunek).
(zobacz rysunek).
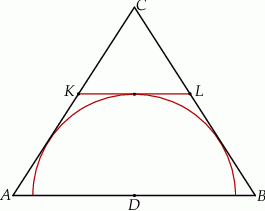
Wykaż, że trójkąt 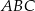 jest równoboczny.
jest równoboczny.
Punkt 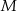 przyprostokątnej
przyprostokątnej 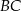 trójkąta prostokątnego
trójkąta prostokątnego 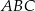 zrzutowano na przeciwprostokątną
zrzutowano na przeciwprostokątną 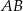 otrzymując punkt
otrzymując punkt 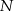 . Wykaż, że
. Wykaż, że 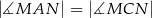 .
.
Dwusieczna kąta 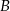 trójkąta
trójkąta 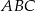 przecina bok
przecina bok 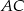 w punkcie
w punkcie 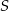 , a dwusieczna kąta
, a dwusieczna kąta 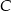 przecina bok
przecina bok 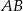 w punkcie
w punkcie 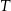 . Dwusieczne przecinają się w punkcie
. Dwusieczne przecinają się w punkcie 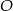 . Znajdź miarę kąta
. Znajdź miarę kąta 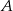 , jeżeli wiadomo, że na czworokącie
, jeżeli wiadomo, że na czworokącie 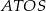 można opisać okrąg.
można opisać okrąg.
Miara jednego z kątów ostrych w trójkącie prostokątnym jest równa  .
.
- Uzasadnij, że spełniona jest nierówność
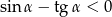 .
. - Dla
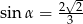 oblicz wartość wyrażenia
oblicz wartość wyrażenia 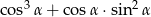 .
.
W trójkącie prostokątnym jedna z przyprostokątnych jest średnią arytmetyczną drugiej przyprostokątnej i przeciwprostokątnej. Oblicz sinusy kątów ostrych tego trójkąta.
W trójkącie prostokątnym stosunek różnicy długości przyprostokątnych do długości przeciwprostokątnej jest równy 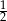 . Oblicz cosinusy kątów ostrych tego trójkąta.
. Oblicz cosinusy kątów ostrych tego trójkąta.
W trójkącie prostokątnym stosunek sumy długości przyprostokątnych do długości przeciwprostokątnej jest równy  . Oblicz cosinusy kątów ostrych tego trójkąta.
. Oblicz cosinusy kątów ostrych tego trójkąta.

