Przeciwprostokątna trójkąta prostokątnego ma długość 26 cm, a jedna z przyprostokątnych jest o 14 cm dłuższa od drugiej. Oblicz obwód tego trójkąta.
/Szkoła średnia/Geometria/Planimetria/Trójkąt
Przeciwprostokątna trójkąta prostokątnego ma długość 34 cm, a jedna z przyprostokątnych jest o 14 cm dłuższa od drugiej. Oblicz obwód tego trójkąta.
Boki trójkąta mają długości 4, 8 i 10.
- Oblicz cosinus i tangens kąta leżącego naprzeciwko najkrótszego boku.
- Oblicz długość środkowej poprowadzonej do najdłuższego boku.
Na okręgu o promieniu 2 opisano trójkąt prostokątny o jednej z przyprostokątnych długości 12. Oblicz obwód tego trójkąta.
Na okręgu o promieniu 3 opisano trójkąt prostokątny o jednej z przyprostokątnych długości 12. Oblicz obwód tego trójkąta.
Dany jest trójkąt ostrokątny równoramienny 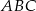 , w którym bok
, w którym bok 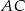 jest równy
jest równy 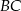 . Odcinek
. Odcinek 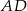 jest wysokością tego trójkąta, oraz odcinek
jest wysokością tego trójkąta, oraz odcinek 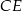 jest wysokością tego trójkąta. Udowodnij, że kąt
jest wysokością tego trójkąta. Udowodnij, że kąt 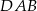 jest równy kątowi
jest równy kątowi 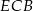 .
.
Na bokach 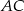 i
i 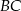 trójkąta
trójkąta 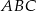 obrano punkty
obrano punkty 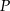 i
i 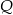 takie, że
takie, że 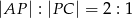 oraz
oraz 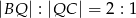 . Odcinki
. Odcinki 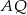 i
i 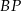 przecinają się w punkcie
przecinają się w punkcie 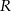 . Wykaż, że pole czworokąta
. Wykaż, że pole czworokąta 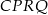 jest równe polu trójkąta
jest równe polu trójkąta 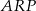 .
.
Długości  i
i 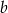 przyprostokątnych trójkąta prostokątnego spełniają równość
przyprostokątnych trójkąta prostokątnego spełniają równość
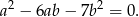
- Oblicz tangensy kątów ostrych tego trójkąta.
- Uzasadnij, że pole tego trójkąta jest równe
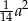 .
.
W trójkąt równoramienny, którego ramię jest równe 5 cm, a podstawa równa się 6 cm, wpisano prostokąt w ten sposób, że dwa jego wierzchołki leżą na podstawie, a pozostałe leżą na ramionach trójkąta. Wyznacz obwód i pole prostokąta jako funkcję jego wysokości.
Na boku 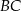 trójkąta równobocznego
trójkąta równobocznego 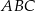 wybrano taki punkt
wybrano taki punkt 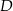 , że pole trójkąta
, że pole trójkąta 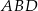 jest równe
jest równe 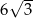 i jest dwa razy większe od pola trójkąta
i jest dwa razy większe od pola trójkąta 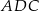 (zobacz rysunek).
(zobacz rysunek).
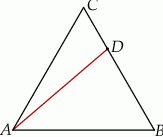
Oblicz długość odcinka 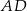 .
.
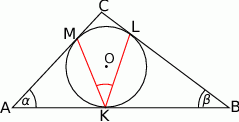
W trójkąt 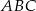 , w którym
, w którym 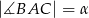 oraz
oraz 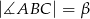 , wpisano okrąg. Punkty
, wpisano okrąg. Punkty 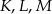 są punktami styczności okręgu odpowiednio z bokami
są punktami styczności okręgu odpowiednio z bokami 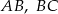 i
i 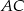 . Wykaż, że
. Wykaż, że 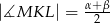 .
.
Proste zawierające wysokości trójkąta ostrokątnego 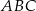 przecinają boki
przecinają boki 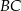 ,
, 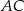 i
i 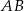 tego trójkąta odpowiednio w punktach
tego trójkąta odpowiednio w punktach 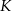 ,
, 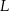 i
i 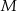 . Wykaż, że jeżeli trójkąt
. Wykaż, że jeżeli trójkąt 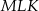 jest podobny do trójkąta
jest podobny do trójkąta 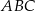 , to trójkąt
, to trójkąt 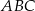 jest równoboczny.
jest równoboczny.
Punkt 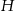 jest punktem wspólnym wysokości trójkąta ostrokątnego
jest punktem wspólnym wysokości trójkąta ostrokątnego 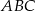 wpisanego w okrąg o promieniu 12. Oblicz promień okręgu opisanego na trójkącie
wpisanego w okrąg o promieniu 12. Oblicz promień okręgu opisanego na trójkącie 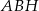 .
.
Oblicz pole trójkąta 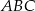 przedstawionego na rysunku, jeśli wiadomo, że
przedstawionego na rysunku, jeśli wiadomo, że 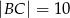 oraz
oraz 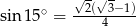 .
.
Wysokości w pewnym trójkącie 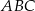 mają długości:
mają długości: 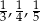 . Wykaż, że jest to trójkąt prostokątny.
. Wykaż, że jest to trójkąt prostokątny.
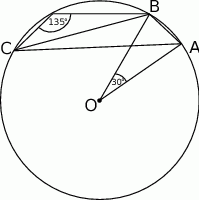
Korzystając z danych przedstawionych na rysunku oblicz wartość wyrażenia
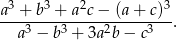
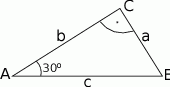
W trójkącie równoramiennym kąt przy podstawie ma miarę  . Oblicz stosunek długości promienia okręgu wpisanego w ten trójkąt do długości promienia okręgu opisanego na nim.
. Oblicz stosunek długości promienia okręgu wpisanego w ten trójkąt do długości promienia okręgu opisanego na nim.
Trójkąty prostokątne 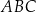 i
i 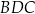 spełniają warunki:
spełniają warunki: 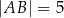 ,
, 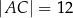 ,
, 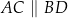 oraz
oraz 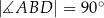 (zobacz rysunek).
(zobacz rysunek).

Oblicz długość odcinka 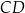 .
.
Dane są dwa trójkąty: 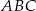 oraz
oraz 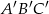 takie, że
takie, że 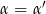 oraz
oraz 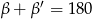 .
.
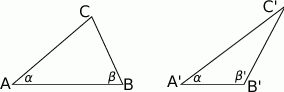
Wykaż, że:
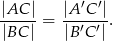
W trójkącie 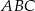 poprowadzono dwusieczne kątów przecinające boki
poprowadzono dwusieczne kątów przecinające boki 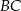 ,
, 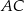 i
i 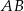 tego trójkąta w punktach – odpowiednio –
tego trójkąta w punktach – odpowiednio – 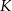 ,
, 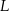 oraz
oraz 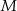 . Punkt
. Punkt 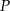 jest punktem przecięcia tych dwusiecznych. Na czworokątach
jest punktem przecięcia tych dwusiecznych. Na czworokątach 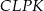 oraz
oraz 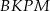 można opisać okrąg. Udowodnij, że trójkąt
można opisać okrąg. Udowodnij, że trójkąt 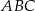 jest równoboczny.
jest równoboczny.
Wykaż, że jeżeli 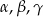 są kątami wewnętrznymi trójkąta i
są kątami wewnętrznymi trójkąta i 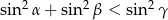 , to
, to 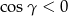 .
.
Wykaż, że jeżeli 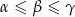 są kątami wewnętrznymi trójkąta rozwartokątnego, to
są kątami wewnętrznymi trójkąta rozwartokątnego, to
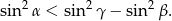
W trójkącie prostokątnym suma cosinusów kątów ostrych jest równa 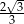 . Wykaż, że iloczyn sinusów tych kątów jest równy
. Wykaż, że iloczyn sinusów tych kątów jest równy 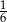 .
.
W trójkącie prostokątnym suma sinusów kątów ostrych jest równa  . Wykaż, że iloczyn cosinusów tych kątów jest równy
. Wykaż, że iloczyn cosinusów tych kątów jest równy  .
.

