Liczby 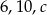 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
/Szkoła średnia/Geometria/Planimetria/Trójkąt
Jeden z kątów trójkąta jest trzy razy większy od mniejszego z dwóch pozostałych kątów, które różnią się o 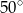 . Oblicz kąty tego trójkąta.
. Oblicz kąty tego trójkąta.
Jeden z kątów trójkąta jest trzy razy większy od drugiego oraz o 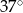 większy od trzeciego kąta. Oblicz miary wszystkich kątów tego trójkąta.
większy od trzeciego kąta. Oblicz miary wszystkich kątów tego trójkąta.
Jeden z kątów trójkąta jest cztery razy mniejszy od mniejszego z dwóch pozostałych kątów, które różnią się o 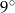 . Oblicz kąty tego trójkąta.
. Oblicz kąty tego trójkąta.
Jeden z kątów trójkąta jest cztery razy większy od drugiego oraz o 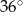 mniejszy od trzeciego kąta. Oblicz miary wszystkich kątów tego trójkąta.
mniejszy od trzeciego kąta. Oblicz miary wszystkich kątów tego trójkąta.
Długości boków trójkąta są w stosunku 2 : 3 : 4. Oblicz wartość wyrażenia
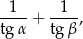
gdzie  oznacza największy, a
oznacza największy, a 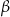 najmniejszy kąt tego trójkąta.
najmniejszy kąt tego trójkąta.
W trójkącie 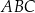 dwusieczna kąta
dwusieczna kąta 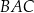 przecina bok
przecina bok 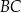 trójkąta w punkcie
trójkąta w punkcie 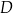 . Wykaż, że
. Wykaż, że
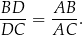
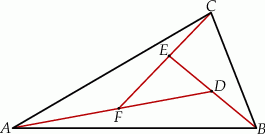
W trójkącie 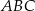 poprowadzono odcinki
poprowadzono odcinki 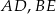 i
i 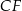 w ten sposób, że punkty
w ten sposób, że punkty 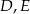 i
i 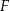 są środkami odpowiednio odcinków
są środkami odpowiednio odcinków 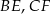 i
i 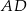 . Oblicz pole trójkąta
. Oblicz pole trójkąta 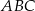 jeżeli pole trójkąta
jeżeli pole trójkąta 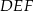 jest równe 2.
jest równe 2.
Trójkąty  i
i  wpisano w ten sam okrąg. Udowodnij, że równość obwodów tych trójkątów jest równoważna równości sum sinusów ich kątów wewnętrznych.
wpisano w ten sam okrąg. Udowodnij, że równość obwodów tych trójkątów jest równoważna równości sum sinusów ich kątów wewnętrznych.
W trójkącie 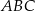 dane są kąt
dane są kąt 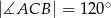 ,
, 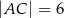 i
i 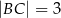 . Dwusieczna kąta
. Dwusieczna kąta 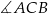 przecina bok
przecina bok 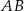 w punkcie
w punkcie 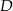 .
.
- Oblicz długość odcinka
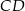 .
. - Jaki jest związek miedzy długościami promieni: okręgu opisanego na trójkącie
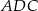 i okręgu opisanego na trójkącie
i okręgu opisanego na trójkącie 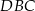 ? Odpowiedź uzasadnij.
? Odpowiedź uzasadnij.
Podstawa trójkąta równoramiennego i środkowe poprowadzone z jej konców mają długość  . Oblicz długość wysokości poprowadzonej do podstawy.
. Oblicz długość wysokości poprowadzonej do podstawy.
W trójkącie równoramiennym 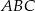 (
(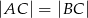 ) dwusieczna
) dwusieczna 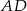 ma długość
ma długość 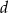 a miara kąta
a miara kąta 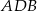 wynosi
wynosi  . Oblicz długość promienia okręgu wpisanego w ten trójkąt.
. Oblicz długość promienia okręgu wpisanego w ten trójkąt.
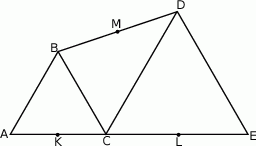
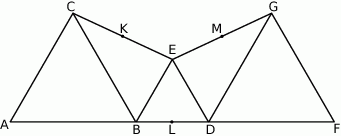
Trójkąty 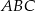 i
i 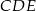 są równoboczne. Punkty
są równoboczne. Punkty 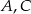 i
i 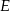 leżą na jednej prostej. Punkty
leżą na jednej prostej. Punkty 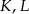 i
i 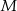 są środkami odcinków
są środkami odcinków 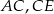 i
i 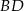 (zobacz rysunek). Wykaż, że punkty
(zobacz rysunek). Wykaż, że punkty 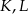 i
i 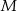 są wierzchołkami trójkąta równobocznego.
są wierzchołkami trójkąta równobocznego.
Trójkąty  i
i  są równoboczne oraz
są równoboczne oraz 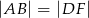 . Punkty
. Punkty 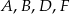 leżą na jednej prostej. Punkty
leżą na jednej prostej. Punkty 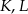 i
i 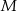 są środkami odcinków
są środkami odcinków 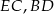 i
i 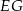 . Wykaż, że punkty
. Wykaż, że punkty 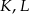 i
i 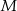 są wierzchołkami trójkąta równobocznego.
są wierzchołkami trójkąta równobocznego.
W trójkącie  miara kąta
miara kąta  jest dwa razy większa od miary kąta
jest dwa razy większa od miary kąta  . Dwusieczna kąta
. Dwusieczna kąta 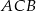 dzieli trójkąt
dzieli trójkąt 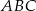 na dwa trójkąty. Uzasadnij, że jeden z otrzymanych trójkątów jest podobny do trójkąta
na dwa trójkąty. Uzasadnij, że jeden z otrzymanych trójkątów jest podobny do trójkąta 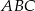 .
.
Dany jest trójkąt prostokątny 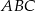 o przeciwprostokątnej
o przeciwprostokątnej 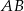 , taki że
, taki że 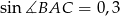 i
i 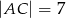 . Oblicz pole koła opisanego na tym trójkącie.
. Oblicz pole koła opisanego na tym trójkącie.
Na trójkącie równoramiennym 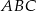 (
(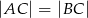 ) o polu równym
) o polu równym 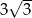 opisano okrąg, którego promień ma długość 2 cm. Oblicz długość wysokości
opisano okrąg, którego promień ma długość 2 cm. Oblicz długość wysokości 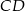 tego trójkąta.
tego trójkąta.
W pewnym trójkącie prostokątnym suma cosinusów kątów ostrych jest równa 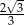 . Oblicz iloczyn sinusów tych kątów.
. Oblicz iloczyn sinusów tych kątów.
Suma sinusów kątów ostrych w pewnym trójkącie prostokątnym wynosi 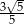 . Oblicz iloczyn sinusów tych kątów.
. Oblicz iloczyn sinusów tych kątów.
Miary kątów trójkąta 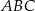 są równe
są równe 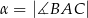 ,
, 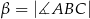 i
i 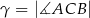 . Punkt
. Punkt 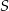 jest środkiem okręgu wpisanego w ten trójkąt, a proste zawierające odcinki
jest środkiem okręgu wpisanego w ten trójkąt, a proste zawierające odcinki 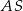 i
i 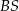 przecinają boki
przecinają boki 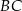 i
i 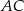 tego trójkąta w punktach odpowiednio
tego trójkąta w punktach odpowiednio 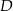 i
i 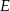 (zobacz rysunek).
(zobacz rysunek).
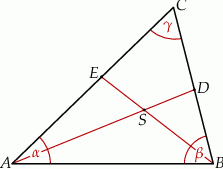
Wykaż, że jeżeli 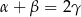 , to na czworokącie
, to na czworokącie 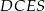 można opisać okrąg.
można opisać okrąg.
Niech  będzie trójkątem równobocznym o boku długości
będzie trójkątem równobocznym o boku długości  . Konstruujemy kolejno trójkąty równoboczne
. Konstruujemy kolejno trójkąty równoboczne 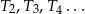 takie, że bok kolejnego trójkąta jest równy wysokości poprzedniego trójkąta. Oblicz sumę pól trójkątów
takie, że bok kolejnego trójkąta jest równy wysokości poprzedniego trójkąta. Oblicz sumę pól trójkątów 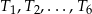 .
.
Dany jest trójkąt 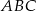 , w którym
, w którym 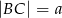 . Z wierzchołka
. Z wierzchołka 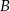 poprowadzono środkową
poprowadzono środkową 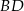 do boku
do boku 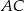 . Punkt
. Punkt 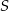 jest środkiem odcinka
jest środkiem odcinka 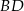 . Przez punkty
. Przez punkty 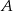 i
i 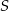 poprowadzono prostą, która przecięła bok
poprowadzono prostą, która przecięła bok 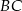 w punkcie
w punkcie 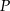 . Wykaż, że długość odcinka
. Wykaż, że długość odcinka 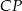 jest równa
jest równa 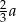 .
.
Dany jest trójkąt 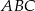 oraz punkt
oraz punkt 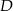 na jego boku
na jego boku 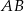 taki, że
taki, że 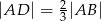 . Z wierzchołka
. Z wierzchołka 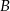 poprowadzono środkową
poprowadzono środkową 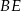 do boku
do boku 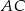 . Punkt
. Punkt 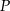 jest punktem wspólnym odcinków
jest punktem wspólnym odcinków 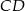 i
i 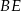 . Wykaż, że punkt
. Wykaż, że punkt 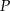 jest środkiem odcinka
jest środkiem odcinka 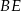 .
.
Wykaż, że jeżeli trójkąt nie jest rozwartokątny, oraz miara  jednego z jego kątów spełnia warunek
jednego z jego kątów spełnia warunek 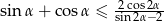 to trójkąt ten jest prostokątny.
to trójkąt ten jest prostokątny.
Odcinek 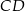 jest wysokością przedstawionego na rysunku trójkąta równoramiennego
jest wysokością przedstawionego na rysunku trójkąta równoramiennego 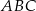 , w którym
, w którym 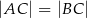 . Punkt
. Punkt 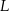 jest rzutem punktu
jest rzutem punktu 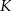 wysokości
wysokości 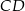 na bok
na bok 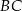 . Udowodnij, że
. Udowodnij, że 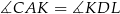 .
.
Odcinek  jest wysokością przedstawionego na rysunku trójkąta równoramiennego
jest wysokością przedstawionego na rysunku trójkąta równoramiennego  , w którym
, w którym 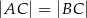 . Punkt
. Punkt 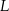 jest rzutem punktu
jest rzutem punktu 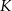 wysokości
wysokości 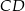 na bok
na bok 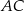 . Udowodnij, że trójkąt
. Udowodnij, że trójkąt 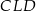 jest podobny do trójkąta
jest podobny do trójkąta 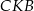 .
.
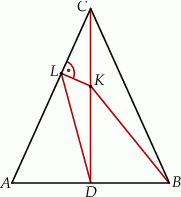
Wierzchołek  trójkąta ostrokątnego
trójkąta ostrokątnego 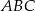 połączono odcinkiem ze środkiem
połączono odcinkiem ze środkiem 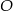 okręgu opisanego. Z wierzchołka
okręgu opisanego. Z wierzchołka 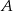 poprowadzono wysokość
poprowadzono wysokość 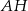 . Wykaż, że
. Wykaż, że 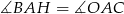 .
.

