Wyznacz wartości funkcji trygonometrycznych kątów ostrych trójkąta powstałego wskutek połączenia odcinkiem wierzchołka kwadratu ze środkiem przeciwległego boku.
/Szkoła średnia/Geometria/Planimetria/Trójkąt
W trójkącie prostokątnym 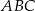 przyprostokątne mają długości:
przyprostokątne mają długości: 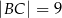 ,
, 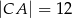 . Na boku
. Na boku 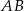 wybrano punkt
wybrano punkt 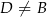 tak, że odcinki
tak, że odcinki 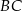 i
i 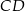 mają równe długości. Oblicz długość odcinka
mają równe długości. Oblicz długość odcinka 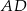 .
.
Trójkąt o bokach 6, 8 i 10 jest podobny do trójkąta o obwodzie 216. Oblicz długości boków drugiego trójkąta.
Trójkąt o bokach 12, 9 i 15 jest podobny do trójkąta o obwodzie 108. Oblicz długości boków drugiego trójkąta.
Wykaż, że w trójkącie prostokątnym suma długości obu przyprostokątnych jest równa sumie długości średnic okręgów wpisanego i opisanego na tym trójkącie.
Przyprostokątne trójkąta prostokątnego mają długości  i
i 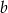 , a jego przeciwprostokątna ma długość
, a jego przeciwprostokątna ma długość  . Wykaż, że promień okręgu wpisanego w ten trójkąt ma długość
. Wykaż, że promień okręgu wpisanego w ten trójkąt ma długość 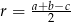 .
.
Trójkąt 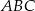 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 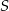 . Kąty wewnętrzne
. Kąty wewnętrzne 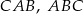 i
i 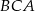 tego trójkąta są równe, odpowiednio,
tego trójkąta są równe, odpowiednio, 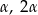 i
i 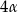 . Wykaż, że trójkąt
. Wykaż, że trójkąt 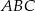 jest rozwartokątny, i udowodnij, że miary wypukłych kątów środkowych
jest rozwartokątny, i udowodnij, że miary wypukłych kątów środkowych 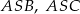 i
i 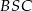 tworzą w podanej kolejności ciąg arytmetyczny.
tworzą w podanej kolejności ciąg arytmetyczny.
Dany jest trójkąt równoboczny 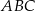 o boku długości 16. Na boku
o boku długości 16. Na boku 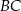 obrano punkt
obrano punkt 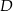 dzielący ten bok w stosunku 3:5, licząc od punktu
dzielący ten bok w stosunku 3:5, licząc od punktu 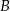 . Oblicz sinus kąta
. Oblicz sinus kąta 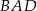 .
.
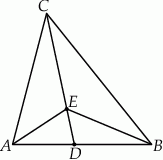
W trójkącie 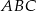 przedłużono bok
przedłużono bok 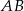 poza wierzchołek
poza wierzchołek 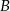 i odłożono odcinek
i odłożono odcinek 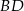 taki, że
taki, że 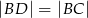 . Następnie połączono punkty
. Następnie połączono punkty 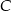 i
i 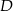 (rysunek). Wykaż, że
(rysunek). Wykaż, że 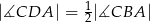 .
.
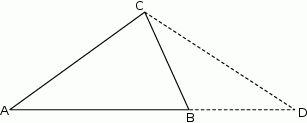
W trójkącie 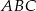 przedłużono bok
przedłużono bok 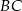 poza wierzchołek
poza wierzchołek 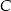 i odłożono odcinek
i odłożono odcinek 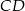 taki, że
taki, że 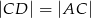 . Następnie połączono punkty
. Następnie połączono punkty 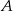 i
i 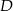 (rysunek). Wykaż, że
(rysunek). Wykaż, że 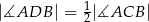 .
.
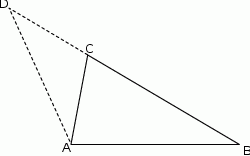
Uzasadnij wzór na pole trójkąta 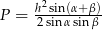 , gdzie
, gdzie  i
i 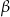 są miarami kątów trójkąta przyległych do boku, na który opuszczono wysokość
są miarami kątów trójkąta przyległych do boku, na który opuszczono wysokość 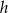 .
.
Trójkąt 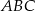 podzielony jest przez dwie proste równoległe do boku
podzielony jest przez dwie proste równoległe do boku 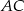 , na trzy figury o równych polach. Oblicz na jakie części proste te podzieliły bok
, na trzy figury o równych polach. Oblicz na jakie części proste te podzieliły bok 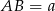 .
.
Na trójkącie o bokach długości 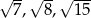 opisano okrąg. Oblicz promień tego okręgu.
opisano okrąg. Oblicz promień tego okręgu.
W trójkącie 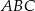 dane są kąty
dane są kąty 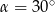 ,
, 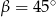 oraz długość
oraz długość  boku leżącego naprzeciw kąta
boku leżącego naprzeciw kąta  . Oblicz długości pozostałych boków.
. Oblicz długości pozostałych boków.
W okrąg o średnicy 16,25 wpisano trójkąt ostrokątny 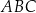 , w którym
, w którym 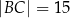 . Miary kątów
. Miary kątów 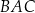 i
i 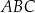 tego trójkąta spełniają warunek
tego trójkąta spełniają warunek
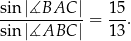
Oblicz promień okręgu wpisanego w trójkąt 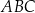 .
.
Na dwusiecznej 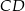 trójkąta
trójkąta 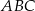 , w którym
, w którym 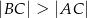 wybrano punkt
wybrano punkt 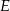 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 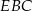 jest większe od pola trójkąta
jest większe od pola trójkąta 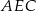 .
.
Dany jest trójkąt o bokach długości 1,  , 2. Oblicz cosinus i sinus kąta leżącego naprzeciw najkrótszego boku tego trójkąta.
, 2. Oblicz cosinus i sinus kąta leżącego naprzeciw najkrótszego boku tego trójkąta.
W trójkącie prostokątnym jedna przyprostokątna jest 4 razy dłuższa od drugiej. Wykaż, że wysokość opuszczona na przeciwprostokątną dzieli ją na odcinki, z których jeden jest 16 razy dłuższy od drugiego.
W trójkącie prostokątnym jedna przyprostokątna jest 3 razy dłuższa od drugiej. Wykaż, że wysokość opuszczona na przeciwprostokątną dzieli ją na odcinki, z których jeden jest 9 razy dłuższy od drugiego.
Dwusieczna kąta prostego w trójkącie prostokątnym dzieli przeciwprostokątna w stosunku 3:4. Oblicz stosunek pola koła opisanego na tym trójkącie do pola koła wpisanego w ten trójkąt.
Kąty 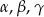 trójkąta
trójkąta 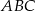 spełniają zależność
spełniają zależność
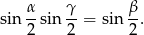
Oblicz wartość wyrażenia 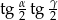 .
.
W trójkącie ostrokątnym 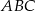 dane są długości boków:
dane są długości boków: 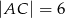 ,
, 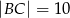 . Pole trójkąta jest równe
. Pole trójkąta jest równe 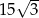 . Oblicz
. Oblicz
- długość boku
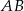 ;
; - sinus kąta
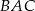 ;
; - pole koła opisanego na trójkącie
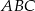 ;
; - długość promienia okręgu wpisanego w trójkąt.
Dany jest trójkąt prostokątny równoramienny 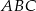 . Punkty
. Punkty 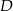 i
i 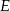 dzielą przeciwprostokątną
dzielą przeciwprostokątną 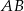 na trzy odcinki równej długości. Oblicz cosinus kąta
na trzy odcinki równej długości. Oblicz cosinus kąta 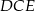 .
.
Dany jest trójkąt 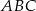 , w którym
, w którym 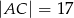 i
i 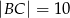 . Na boku
. Na boku 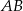 leży punkt
leży punkt 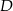 taki, że
taki, że 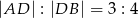 oraz
oraz 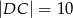 . Oblicz pole trójkąta
. Oblicz pole trójkąta 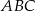 .
.

