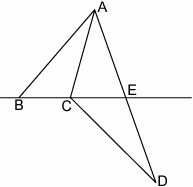
Wiedząc, że punkt 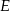 jest środkiem odcinka
jest środkiem odcinka 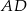 , a punkt
, a punkt 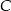 jest środkiem odcinka
jest środkiem odcinka 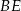 oraz
oraz 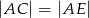 , wykaż, że
, wykaż, że 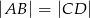 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wiedząc, że punkt 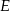 jest środkiem odcinka
jest środkiem odcinka 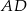 , a punkt
, a punkt 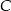 jest środkiem odcinka
jest środkiem odcinka 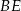 oraz
oraz 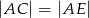 , wykaż, że
, wykaż, że 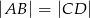 .
.

W trójkącie 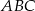 na boku
na boku 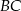 zaznaczono punkt
zaznaczono punkt 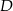 , na boku
, na boku 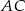 zaznaczono punkt
zaznaczono punkt 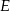 , na boku
, na boku 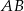 punkt
punkt 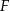 . Poprowadzono okręgi
. Poprowadzono okręgi 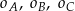 , w ten sposób, że do okręgu
, w ten sposób, że do okręgu 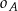 należą punkty
należą punkty 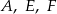 , do
, do 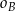 – punkty
– punkty 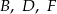 , a do
, a do 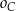 – punkty
– punkty 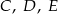 . Wykaż, że te trzy okręgi przecinają się w jednym punkcie.
. Wykaż, że te trzy okręgi przecinają się w jednym punkcie.
Okrąg 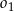 przechodzi przez wierzchołek
przechodzi przez wierzchołek 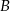 trójkąta
trójkąta 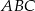 i przecina jego boki
i przecina jego boki 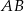 i
i 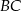 odpowiednio w punktach
odpowiednio w punktach 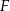 i
i 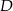 . Okrąg
. Okrąg 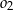 przechodzi przez wierzchołek
przechodzi przez wierzchołek 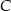 , przecina okrąg
, przecina okrąg 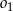 w punkcie
w punkcie 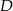 oraz w punkcie
oraz w punkcie 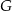 leżącym wewnątrz trójkąta
leżącym wewnątrz trójkąta 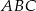 . Ponadto okrąg
. Ponadto okrąg 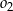 przecina bok
przecina bok 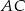 trójkąta w punkcie
trójkąta w punkcie 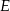 .
.
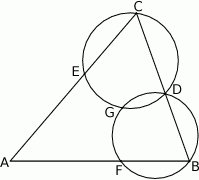
Udowodnij, że punkt 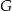 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 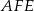 .
.
W trójkącie 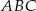 dane są:
dane są: 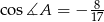 ,
, 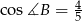 i
i 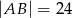 . Oblicz długości pozostałych boków trójkąta
. Oblicz długości pozostałych boków trójkąta 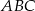 .
.
W trójkącie 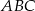 dane są długości boków:
dane są długości boków: 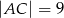 ,
, 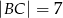 . Wiadomo też, że miara kąta
. Wiadomo też, że miara kąta 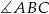 jest dwa razy większa od miary kąta
jest dwa razy większa od miary kąta 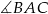 . Oblicz stosunek długości promienia okręgu wpisanego w ten trójkąt do długości promienia okręgu opisanego na tym trójkącie.
. Oblicz stosunek długości promienia okręgu wpisanego w ten trójkąt do długości promienia okręgu opisanego na tym trójkącie.
Pole prostokąta 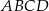 jest równe 60, a promień okręgu wpisanego w trójkąt
jest równe 60, a promień okręgu wpisanego w trójkąt 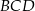 jest równy 2. Oblicz obwód tego prostokąta.
jest równy 2. Oblicz obwód tego prostokąta.
W trójkącie 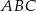 na boku
na boku 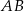 wybrano takie punkty
wybrano takie punkty 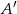 i
i 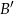 , że
, że
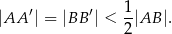
Przez punkty 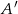 i
i 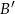 poprowadzono proste równoległe do boków odpowiednio
poprowadzono proste równoległe do boków odpowiednio 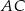 i
i 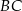 . Proste te przecięły się w punkcie
. Proste te przecięły się w punkcie 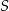 . Wykaż, że odcinek
. Wykaż, że odcinek 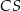 jest zawarty w środkowej trójkąta
jest zawarty w środkowej trójkąta 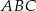 .
.
Środek okręgu opisanego na trójkącie prostokątnym leży w odległości 3 cm i 2 cm od przyprostokątnych. Oblicz pole tego trójkąta.
Okrąg wpisany w trójkąt prostokątny 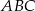 o bokach długości
o bokach długości 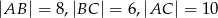 jest styczny do boków
jest styczny do boków 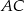 i
i 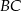 w punktach
w punktach 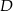 i
i 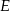 . Proste
. Proste 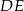 i
i 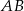 przecinają się punkcie
przecinają się punkcie 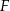 . Oblicz pole trójkąta
. Oblicz pole trójkąta 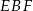 .
.
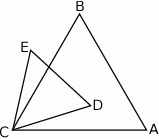
Trójkąty równoboczne 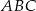 i
i 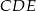 są położone tak, jak na poniższym rysunku. Wykaż, że
są położone tak, jak na poniższym rysunku. Wykaż, że 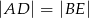 .
.
W trójkącie prostokątnym, w którym przyprostokątne mają długości 2 i 4, jeden z kątów ostrych ma miarę  . Oblicz
. Oblicz 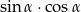 .
.
W trójkącie prostokątnym przyprostokątne mają długości 2 i 4, a jeden z kątów ostrych ma miarę  . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 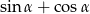 .
.
W trójkącie prostokątnym przyprostokątne mają długości 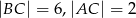 . Wyznacz wartość wyrażenia
. Wyznacz wartość wyrażenia 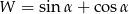 , gdzie
, gdzie  jest najmniejszym kątem ostrym tego trójkąta.
jest najmniejszym kątem ostrym tego trójkąta.
W trójkącie prostokątnym przyprostokątne mają długości 3 i 5, a jeden z kątów ostrych ma miarę  . Oblicz
. Oblicz 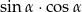 .
.
W trójkącie prostokątnym przyprostokątne mają długości 1 i 3, a jeden z kątów ostrych ma miarę  . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 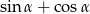 .
.
Trójkąt równoboczny 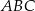 ma pole równe
ma pole równe 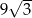 . Prosta równoległa do boku
. Prosta równoległa do boku 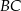 przecina boki
przecina boki 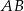 i
i 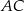 – odpowiednio – w punktach
– odpowiednio – w punktach 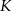 i
i 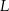 . Trójkąty
. Trójkąty 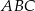 i
i 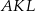 są podobne, a stosunek długości boków tych trójkątów jest równy
są podobne, a stosunek długości boków tych trójkątów jest równy  . Oblicz długość boku trójkąta
. Oblicz długość boku trójkąta 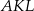 .
.
Trójkąt równoboczny 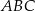 ma pole równe
ma pole równe 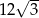 . Prosta równoległa do boku
. Prosta równoległa do boku 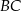 przecina boki
przecina boki 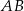 i
i 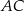 – odpowiednio – w punktach
– odpowiednio – w punktach 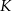 i
i 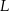 . Stosunek obwodów trójkątów
. Stosunek obwodów trójkątów 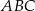 i
i 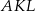 jest równy
jest równy 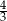 . Oblicz długość boku trójkąta
. Oblicz długość boku trójkąta 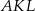 .
.
W trójkącie rozwartokątnym 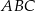 o kącie rozwartym przy wierzchołku
o kącie rozwartym przy wierzchołku 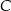 poprowadzono wysokość
poprowadzono wysokość 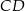 i otrzymano równoramienny trójkąt
i otrzymano równoramienny trójkąt 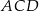 . Długości boków
. Długości boków 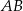 i
i 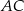 są odpowiednio równe
są odpowiednio równe 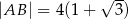 i
i 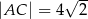 . Oblicz pole powierzchni koła opisanego na trójkącie
. Oblicz pole powierzchni koła opisanego na trójkącie 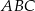 .
.
Na ramionach 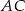 i
i 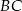 trójkąta równoramiennego
trójkąta równoramiennego 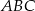 wybrano punkty
wybrano punkty 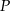 i
i 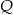 w ten sposób, że odcinek
w ten sposób, że odcinek 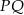 jest równoległy do podstawy
jest równoległy do podstawy 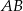 i styczny do okręgu wpisanego w trójkąt
i styczny do okręgu wpisanego w trójkąt 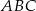 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 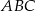 jest równe
jest równe
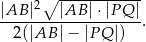
Punkty 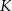 i
i 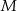 oraz
oraz 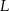 i
i 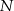 dzielą odpowiednio boki
dzielą odpowiednio boki 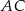 i
i 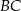 trójkąta
trójkąta 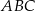 w stosunku
w stosunku 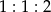 (zobacz rysunek). Odcinki
(zobacz rysunek). Odcinki 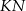 i
i 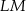 przecinają się w punkcie
przecinają się w punkcie 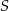 .
.
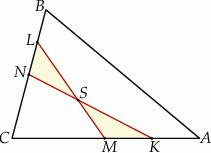
Uzasadnij, że pola trójkątów 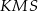 i
i 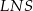 są równe.
są równe.
W trójkącie 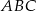 , w którym
, w którym 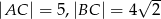 i
i 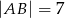 na boku
na boku 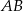 wybrano taki punkt
wybrano taki punkt 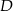 , że
, że 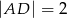 . Oblicz sinus kąta
. Oblicz sinus kąta 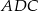 .
.
W trójkącie prostokątnym 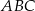 (
(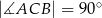 ,
, 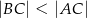 ) poprowadzono prostą przechodzącą przez wierzchołek
) poprowadzono prostą przechodzącą przez wierzchołek 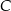 trójkąta która przecina przeciwprostokątną w punkcie
trójkąta która przecina przeciwprostokątną w punkcie 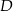 , takim, że
, takim, że 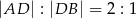 . Oblicz długość przeciwprostokątnej jeśli
. Oblicz długość przeciwprostokątnej jeśli 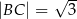 i
i 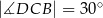 .
.
Środkowa 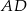 trójkąta równoramiennego
trójkąta równoramiennego 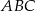 ma długość
ma długość 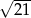 , a jego podstawa
, a jego podstawa 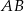 tworzy z ramieniem kąt o mierze
tworzy z ramieniem kąt o mierze 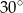 . Oblicz pole trójkąta
. Oblicz pole trójkąta 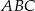 .
.
W trójkącie 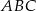 mamy dane
mamy dane 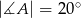 oraz
oraz 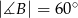 . Punkt
. Punkt 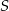 jest środkiem okręgu opisanego na tym trójkącie. Oblicz miary kątów
jest środkiem okręgu opisanego na tym trójkącie. Oblicz miary kątów 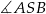 ,
, 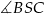 i
i 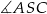 .
.
Wyznacz długości boków oraz miary kątów trójkąta prostokątnego jeżeli 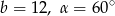 .
.
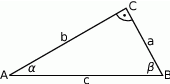
Wyznacz długości boków oraz miary kątów trójkąta prostokątnego jeżeli 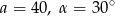 .
.
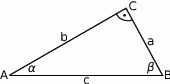
Wykaż, że jeżeli 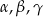 są kątami wewnętrznymi trójkąta i
są kątami wewnętrznymi trójkąta i 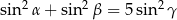 , to
, to 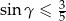 .
.
