Dany jest prostokąt 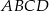 . Okręgi o średnicach
. Okręgi o średnicach 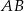 i
i 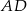 przecinają się w punktach
przecinają się w punktach 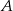 i
i  .
.
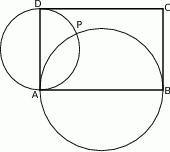
Wykaż, że punkty 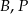 i
i 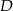 leżą na jednej prostej.
leżą na jednej prostej.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest prostokąt 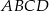 . Okręgi o średnicach
. Okręgi o średnicach 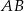 i
i 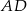 przecinają się w punktach
przecinają się w punktach 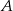 i
i 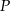 .
.

Wykaż, że punkty 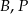 i
i 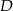 leżą na jednej prostej.
leżą na jednej prostej.
Punkty 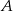 i
i 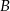 są punktami wspólnymi dwóch okręgów, a odcinki
są punktami wspólnymi dwóch okręgów, a odcinki 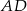 i
i 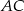 ich średnicami.
ich średnicami.
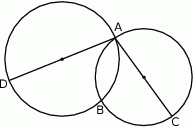
Wykaż, że punkt 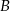 leży na prostej przechodzącej przez punkty
leży na prostej przechodzącej przez punkty 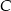 i
i 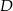 .
.
Dany jest równoległobok 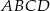 . Okręgi o średnicach
. Okręgi o średnicach 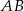 i
i 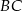 przecinają się w punktach
przecinają się w punktach 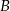 i
i 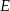 .
.
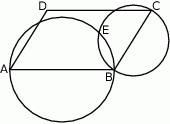
Wykaż, że punkty 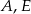 i
i 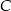 leżą na jednej prostej.
leżą na jednej prostej.
Dane są cztery okręgi. Każdy z nich jest styczny zewnętrznie do dokładnie dwóch spośród trzech pozostałych okręgów. Udowodnij, że punkty styczności tych okręgów są wierzchołkami czworokąta, na którym można opisać okrąg.
Dane są dwa kąty wpisane oparte na tym samym łuku. Wykaż, że dwusieczne tych kątów przetną się w punkcie należącym do okręgu.
W okręgu narysowano dwie średnice 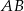 i
i 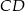 . Udowodnij, że czworokąt
. Udowodnij, że czworokąt 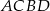 jest prostokątem.
jest prostokątem.
Dane są cztery okręgi. Każdy z nich jest styczny zewnętrznie do dokładnie dwóch spośród trzech pozostałych okręgów. Uzasadnij, że środki tych okręgów są wierzchołkami czworokąta, w który można wpisać okrąg.
Na okręgu wybrano takich pięć różnych punktów: 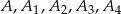 , że
, że
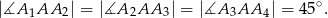
Udowodnij, że punkty 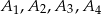 są wierzchołkami kwadratu.
są wierzchołkami kwadratu.
