Z definicji/Prawdopodobieństwo - zadania z matematyki

/Szkoła średnia/Prawdopodobieństwo/Z definicji

Losujemy jedną z 52 kart. Jakie jest prawdopodobieństwo wyciągnięcia asa lub króla?

Ukryj Podobne zadania

Losujemy jedną z 52 kart. Jakie jest prawdopodobieństwo wyciągnięcia kiera?

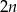W urnie znajduje się kul czarnych i kul białych ( 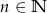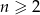n ∈ N , n ≥ 2 ). Losujemy jednocześnie dwie kule. Dla jakich prawdopodobieństwo wylosowania dwóch kul tego samego koloru jest większe od prawdopodobieństwa wylosowania dwóch kul różnych kolorów?

Rzucamy 9 razy symetryczną 6-ścienną kostką do gry. Jakie jest prawdopodobieństwo, że w każdych trzech kolejnych rzutach otrzymamy trzy różne liczby oczek?

Mamy 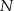pałek o jednakowej długości. Każdą z nich łamiemy na 2 części: długą i krótką. 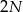części połączono losowo w 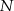par, z których utworzono nowe pałki. Wyznacz prawdopodobieństwo tego, że:

części zostaną połączone tak, jak przed złamaniem;
wszystkie długie części będą połączone z krótkimi.

Grupę uczniów ustawiono w dwuszeregu: w pierwszym szeregu ustawiono 8 osób, a w drugim 10. Jakie jest prawdopodobieństwo zdarzenia polegającego na tym, że dwie losowo wybrane osoby stoją w tym samym szeregu i obok siebie?

Ze zbioru liczb 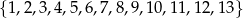{1,2,3,4 ,5,6,7,8,9,10,11 ,1 2,13} losujemy bez zwracania 4 liczby. Oblicz jakie jest prawdopodobieństwo, że wśród 4 otrzymanych liczb jest dokładnie jedna para liczb o sumie równej 14.

Ze zbioru liczb 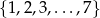{1,2,3,...,7 } losujemy kolejno dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo wylosowania liczb, których suma jest podzielna przez 3.

Ukryj Podobne zadania

Ze zbioru liczb 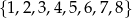{1,2,3,4 ,5,6,7,8} losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 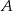, polegającego na wylosowaniu liczb, których iloczyn jest podzielny przez 8.

Ze zbioru liczb 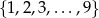{1,2,3,...,9 } losujemy kolejno dwa razy po jednej liczbie (liczby mogą się powtarzać). Oblicz prawdopodobieństwo wylosowania liczb, których suma jest podzielna przez 5.

Ze zbioru liczb 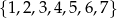{1,2,3 ,4 ,5,6,7} losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 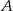, polegającego na wylosowaniu liczb, których iloczyn jest podzielny przez 6.

Spośród cyfr 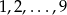1,2,...,9 losujemy bez zwracania dwie i tworzymy z nich liczbę dwucyfrową, której cyfrą dziesiątek jest pierwsza z wylosowanych cyfr. Oblicz prawdopodobieństwo że otrzymana liczba jest parzysta.

Do windy na parterze budynku wsiadło 6 osób, po czym każda z nich w sposób losowy wysiadła na jednym z trzech pięter budynku. Jakie jest prawdopodobieństwo, że na jednym z pięter wysiadły dokładnie 4 osoby?

Umieszczamy króla szachowego w lewym dolnym rogu 64-polowej szachownicy, a następnie siedem razy przesuwamy go losowo w górę lub w prawo (za każdym razem na nowo losujemy kierunek przesunięcia).

Zakładając, że wylosowanie każdego kierunku jest jednakowo prawdopodobne, oblicz prawdopodobieństwo, że na końcu król nie znajdzie się w rogu szachownicy.

Rzucamy trzy razy kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w trzecim rzucie otrzymamy dwa razy więcej oczek niż w pierwszym rzucie.

Ukryj Podobne zadania

Rzucamy trzy razy kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w pierwszym rzucie otrzymamy dwa razy więcej oczek niż w trzecim rzucie.

W pudełku są cztery kartki, na których wypisano liczby 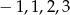− 1,1,2,3 (na każdej kartce jedną liczbę). Losujemy jedną kartkę, zapisujemy liczbę i zwracamy kartkę do pudełka. Następnie losujemy drugą kartkę i zapisujemy liczbę. Wylosowane liczby tworzą parę 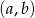(a,b) , gdzie jest liczbą wylosowaną za pierwszym razem, zaś 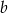liczbą wylosowaną za drugim razem. Oblicz prawdopodobieństwo zdarzenia

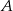– iloczyn wylosowanych liczb jest liczbą pierwszą;
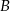– różnica wylosowanych liczb jest liczbą parzystą.

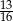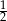W urnie znajdują się drewniane klocki, przy czym każdy z klocków jest biały lub czarny oraz każdy z klocków ma kształt kuli lub sześcianu. Wiadomo, że prawdopodobieństwo wylosowania czarnego klocka jest równe 1316- , prawdopodobieństwo wylosowania klocka w kształcie sześcianu jest równe 5 8 , a prawdopodobieństwo wylosowania klocka, który jest biały lub jest kulą jest równe 1 2 . Oblicz prawdopodobieństwo wybrania klocka, który jest białą kulą.

Z pewnej grupy osób, w której jest dwa razy więcej mężczyzn niż kobiet, wybrano losowo dwuosobową delegację. Prawdopodobieństwo tego, że w delegacji znajdą się tylko kobiety jest równe 0,1. Oblicz, ile kobiet i ilu mężczyzn jest w tej grupie.

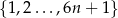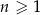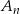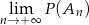Ze zbioru liczb {1,2 ...,6n + 1} , n ≥ 1 losujemy kolejno trzy razy po jednej liczbie bez zwracania. Niech oznacza zdarzenie polegające na tym, że iloczyn wylosowanych liczb jest podzielny przez 6. Oblicz granicę lim P(An ) n→+ ∞ .

Z talii 52 kart losujemy bez zwracania dwie karty. Jakie jest prawdopodobieństwo wylosowania dwóch asów?

Ukryj Podobne zadania

Z talii 52 kart losujemy bez zwracania dwie karty. Jakie jest prawdopodobieństwo wylosowania asa i króla?

Z talii 52 kart losujemy bez zwracania dwie karty. Jakie jest prawdopodobieństwo wylosowania dwóch kierów?

W urnie jest 2 razy więcej kul czarnych niż białych i 3 razy więcej kul zielonych niż białych. Przy losowaniu 3 kul z tej urny prawdopodobieństwo wylosowania 3 kul różnych kolorów wynosi 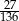21736 . Jakie jest prawdopodobieństwo wylosowania z urny 3 kul, wśród których dokładnie 2 będą tego samego koloru.

Rzucamy dwiema sześciennymi kostkami. Jakie jest prawdopodobieństwo, że na pierwszej kostce wypadło dwa razy mniej oczek niż na drugiej?

Ukryj Podobne zadania

Rzucamy dwiema sześciennymi kostkami. Jakie jest prawdopodobieństwo, że na obu kostkach będzie ta sama liczba oczek?

Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia 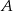polegającego na tym, że liczba oczek w drugim rzucie jest o 1 większa od liczby oczek w pierwszym rzucie.

Rzucamy dwa razy kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w pierwszym rzucie wypadnie podzielna przez 3 liczba oczek.

Rzucamy dwukrotnie sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma liczb oczek otrzymanych na obu kostkach jest większa od 6 i iloczyn tych liczb jest nieparzysty.

Rzucamy dwiema sześciennymi kostkami. Jakie jest prawdopodobieństwo, że co najmniej na jednej kostce będzie jedynka?

Rzucamy dwiema sześciennymi kostkami. Jakie jest prawdopodobieństwo, że na każdej kostce będzie co najmniej 5 oczek?

Rzucamy dwiema sześciennymi kostkami. Jakie jest prawdopodobieństwo, że suma oczek będzie równa 4?

Rzucamy czerwoną i zieloną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na wyrzuceniu takiej samej liczby oczek na obu kostkach.

Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo otrzymania iloczynu oczek równego 6.

Gracz rzuca dwukrotnie symetryczną sześcienną kostką do gry i oblicza sumę liczb wyrzuconych oczek. Oblicz prawdopodobieństwo zdarzenia 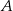polegającego na tym, że suma liczb wyrzuconych oczek jest równa 4 lub 5, lub 6.

Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo otrzymania iloczynu oczek równego 5.

Gracz rzuca dwukrotnie symetryczną sześcienną kostką do gry i oblicza wartość bezwzględną różnicy liczb wyrzuconych oczek. Oblicz prawdopodobieństwo zdarzenia 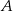polegającego na tym, że obliczona wartość bezwzględna różnicy wyrzuconych oczek jest równa 3, 4 lub 5.

Rzucamy dwa razy kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w drugim rzucie wypadnie parzysta liczba oczek.

Każdy z trojga chłopców pomyślał sobie liczbę dwucyfrową. Jakie jest prawdopodobieństwo, że żadne dwie z tych osób nie pomyślały tej samej liczby? Wynik podaj w postaci ułamka nieskracalnego.

Z cyfr 0, 1, 2, 3, 4 układamy wszystkie możliwe liczby trzycyfrowe o różnych cyfrach. Ze zbioru takich liczb losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia 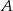– wybrana liczba trzycyfrowa ma tę własność, że cyfry: setek, dziesiątek oraz jedności (w podanej kolejności) tworzą ciąg arytmetyczny.

Strona 7 z 16