Ze zbioru liczb 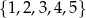 losujemy kolejno trzy razy po jednej liczbie ze zwracaniem tworząc liczbę trzycyfrową. Oblicz prawdopodobieństwo zdarzenia
losujemy kolejno trzy razy po jednej liczbie ze zwracaniem tworząc liczbę trzycyfrową. Oblicz prawdopodobieństwo zdarzenia 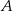 – otrzymana liczba jest cztery razy większa od kwadratu liczby naturalnej.
– otrzymana liczba jest cztery razy większa od kwadratu liczby naturalnej.
/Szkoła średnia/Prawdopodobieństwo/Z definicji
W urnie znajduje się 20 kul: 9 białych, 9 czerwonych i 2 zielone. Z tej urny losujemy bez zwracania 3 kule. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że co najmniej dwie z wylosowanych kul są tego samego koloru.
W urnie jest dziesięć kul różniących się wyłącznie kolorem: 4 czarne, 3 białe, 2 zielone i 1 niebieska. Losujemy jednocześnie trzy kule z urny. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że przynajmniej dwie z wylosowanych kul mają ten sam kolor.
W jednej urnie jest 5 kul białych i pewna liczba kul czarnych, w drugiej zaś 6 kul czarnych i pewna liczba kul białych. Z każdej urny losujemy po dwie kule. Prawdopodobieństwo wylosowania jednocześnie dwóch kul białych z pierwszej urny jest większe od  , a prawdopodobieństwo jednoczesnego wylosowania dwóch kul czarnych z drugiej urny jest większe od
, a prawdopodobieństwo jednoczesnego wylosowania dwóch kul czarnych z drugiej urny jest większe od 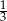 . W której urnie jest więcej kul białych, a w której czarnych?
. W której urnie jest więcej kul białych, a w której czarnych?
W każdym z dwóch pudełek znajduje się tyle samo kul. Kule te są w jednym z dwóch kolorów: czarne lub białe. Prawdopodobieństwo wylosowania kuli białej z pierwszego pudełka jest równe 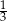 i jest dwa razy większe niż prawdopodobieństwo wylosowania kuli czarnej z drugiego pudełka. Umieszczamy teraz wszystkie kule z tych dwóch pudełek w jednym trzecim pudełku. Jakie jest prawdopodobieństwo wylosowania kuli białej z trzeciego pudełka?
i jest dwa razy większe niż prawdopodobieństwo wylosowania kuli czarnej z drugiego pudełka. Umieszczamy teraz wszystkie kule z tych dwóch pudełek w jednym trzecim pudełku. Jakie jest prawdopodobieństwo wylosowania kuli białej z trzeciego pudełka?
Spośród liczb: -9, -7, -5, -3, -1, 0, 2, 4, 6, 8 losujemy dwie różne liczby  i
i 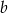 , a następnie zapisujemy ich iloczyn
, a następnie zapisujemy ich iloczyn 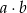 . Oblicz i porównaj prawdopodobieństwa zdarzeń
. Oblicz i porównaj prawdopodobieństwa zdarzeń 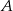 i
i 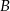 , jeśli:
, jeśli: 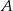 oznacza zdarzenie, że iloczyn
oznacza zdarzenie, że iloczyn 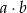 jest liczbą nieujemną;
jest liczbą nieujemną; 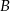 – zdarzenie, że iloczyn
– zdarzenie, że iloczyn 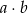 jest liczbą niedodatnią.
jest liczbą niedodatnią.
Ze zbioru 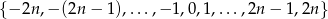 losujemy ze zwracaniem dwie liczby:
losujemy ze zwracaniem dwie liczby:  i
i 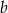 . Rozważmy zdarzenia
. Rozważmy zdarzenia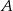 :
: 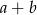 jest liczbą parzystą;
jest liczbą parzystą;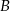 :
: 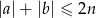 .
.
Oblicz prawdopodobieństwo zdarzenia 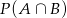 .
.
Z talii 52 kart losujemy jedną kartę.
- Oblicz prawdopodobieństwo zdarzeń:
A – losowo wybrana karta jest pikiem.
B – losowo wybrana karta jest asem. - Oblicz prawdopodobieństwo zdarzeń
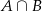 oraz
oraz 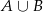 .
.
Rzucamy dwukrotnie kostką, które ze zdarzeń jest bardziej prawdopodobne: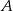 – w pierwszym rzucie otrzymamy liczbę oczek mniejszą niż w drugim;
– w pierwszym rzucie otrzymamy liczbę oczek mniejszą niż w drugim;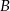 – suma oczek, jakie wypadną w obydwu rzutach, jest nie mniejsza od 8?
– suma oczek, jakie wypadną w obydwu rzutach, jest nie mniejsza od 8?
Dany jest zbiór 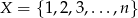 ,
, 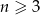 ,
, 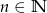 . Ze zbioru
. Ze zbioru 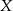 losujemy kolejno bez zwracania dwie liczby. Oblicz prawdopodobieństwo, że pierwsza z wylosowanych liczb jest większa od drugiej.
losujemy kolejno bez zwracania dwie liczby. Oblicz prawdopodobieństwo, że pierwsza z wylosowanych liczb jest większa od drugiej.
Zakupiono 16 biletów do teatru, w tym 10 biletów na miejsca od 1. do 10. w pierwszym rzędzie i 6 biletów na miejsca od 11. do 16. w szesnastym rzędzie. Jakie jest prawdopodobieństwo zdarzenia polegającego na tym, że 2 wylosowane bilety, spośród szesnastu, będą biletami na sąsiadujące miejsca?
Ze zbioru 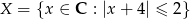 losujemy dwa razy (bez zwracania) po jednej liczbie. Oznaczamy te liczby w kolejności losowania przez
losujemy dwa razy (bez zwracania) po jednej liczbie. Oznaczamy te liczby w kolejności losowania przez  oraz
oraz 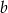 . Oblicz prawdopodobieństwo tego, że wylosowana para liczb
. Oblicz prawdopodobieństwo tego, że wylosowana para liczb 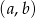 jest rozwiązaniem nierówności
jest rozwiązaniem nierówności 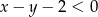 .
.
Doświadczenie losowe polega na trzykrotnym rzucie symetryczną monetą. Jakie jest prawdopodobieństwo, że wylosujemy co najmniej dwa razy orła?
Doświadczenie losowe polega na trzykrotnym rzucie symetryczną monetą. Jakie jest prawdopodobieństwo, że wylosujemy dokładnie dwa razy orła?
Rzucamy pięć razy symetryczną monetą. Po przeprowadzonym doświadczeniu zapisujemy liczbę uzyskanych orłów (od 0 do 5) i liczbę uzyskanych reszek (również od 0 do 5). Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w tych pięciu rzutach liczba uzyskanych orłów będzie mniejsza niż liczba uzyskanych reszek.
Rzucamy cztery razy symetryczną monetą. Po przeprowadzonym doświadczeniu zapisujemy liczbę uzyskanych orłów (od 0 do 4) i liczbę uzyskanych reszek (również od 0 do 4). Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w tych czterech rzutach liczba uzyskanych orłów będzie większa niż liczba uzyskanych reszek.
Ze zbioru wszystkich trójwyrazowych ciągów o wyrazach ze zbioru 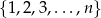 losujemy jeden ciąg.
losujemy jeden ciąg.
- Oblicz prawdopodobieństwo wylosowania ciągu rosnącego lub malejącego.
- Dla jakiej liczby naturalnej
 prawdopodobieństwo to jest równe 0,125?
prawdopodobieństwo to jest równe 0,125?
Liczby 1, 2, 3, 4, 5, 6, 7, 8 ustawiamy losowo w szeregu. Oblicz prawdopodobieństwo, że w tym ustawieniu suma każdych dwóch sąsiednich liczb będzie nieparzysta. Wynik podaj w postaci ułamka nieskracalnego.
Z urny zawierającej 8 kul białych i 4 czarne wylosowano bez zwracania 5 kul. Jakie jest prawdopodobieństwo tego, że stosunek liczby kul czarnych do liczby kul białych w urnie uległ zwiększeniu?
Z urny zawierającej 7 kul białych i 3 kule czarne wylosowano bez zwracania 4 kule. Jakie jest prawdopodobieństwo tego, że stosunek liczby kul czarnych do liczby kul białych w urnie uległ zwiększeniu?
Do windy na parterze budynku wsiadło 6 osób, po czym każda z nich w sposób losowy wysiadła na jednym z trzech pięter budynku. Jakie jest prawdopodobieństwo, że na żadnym z pięter nie wysiadły więcej niż 4 osoby?
Losujemy jedną liczbę spośród liczb: 1, 2, 3,…, 1000. Oblicz prawdopodobieństwo wylosowania liczby podzielnej przez 4 lub przez 9.
Spośród liczb: 0, 1, 2, 3, 4, 5,…, 1000 wybieramy losowo jedną liczbę. Oblicz prawdopodobieństwo zdarzenia, że liczba ta jest podzielna przez 4 lub 5.
Ze zbioru liczb trzycyfrowych mniejszych od 500 wybieramy losowo jedną liczbę. Jakie jest prawdopodobieństwo, że będzie to liczba podzielna przez 3 lub przez 5?
Ze zbioru 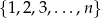 losujemy bez zwracania parę liczb
losujemy bez zwracania parę liczb 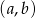 . Dla jakich
. Dla jakich  prawdopodobieństwo wylosowania pary spełniającej warunek
prawdopodobieństwo wylosowania pary spełniającej warunek 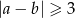 jest większe od
jest większe od 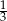 ?
?
W urnie jest 16 kul ponumerowanych liczbami od 1 do 16. Kule z numerami od 1 do 3 są białe, z numerami od 4 do 7 czerwone, a pozostałe są zielone. Losujemy jedną kulę. Oblicz prawdopodobieństwo tego, że wylosowana kula jest czerwona lub zielona.
W urnie jest 16 kul ponumerowanych liczbami od 1 do 16. Kule z numerami od 1 do 3 są białe, z numerami od 4 do 7 czerwone, a pozostałe są zielone. Losujemy jedną kulę. Oblicz prawdopodobieństwo tego, że wylosowano kulę czerwoną lub kulę z numerem parzystym.
W urnie jest 16 kul ponumerowanych liczbami od 1 do 16. Kule z numerami od 1 do 3 są białe, z numerami od 4 do 7 czerwone, a pozostałe są zielone. Losujemy jedną kulę. Oblicz prawdopodobieństwo tego, że numer wylosowanej kuli jest podzielny przez 3.
W urnie jest 16 kul ponumerowanych liczbami od 1 do 16. Kule z numerami od 1 do 3 są białe, z numerami od 4 do 7 czerwone, a pozostałe są zielone. Losujemy jedną kulę. Oblicz prawdopodobieństwo tego, że wylosowano kulę zieloną z numerem dwucyfrowym.
Dane są dwa pudełka: czerwone i niebieskie. W każdym z tych pudełek znajduje się 10 kul ponumerowanych liczbami od 1 do 10. Z każdego pudełka losujemy jedną kulę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że numer kuli wylosowanej z czerwonego pudełka jest mniejszy od numeru kuli wylosowanej z niebieskiego pudełka.

