Rzucono 8 razy monetą. Oblicz prawdopodobieństwo tego, że co najmniej jeden raz wyrzucono orła.
/Szkoła średnia/Prawdopodobieństwo/Z definicji
Rzucono 8 razy monetą. Oblicz prawdopodobieństwo tego, że dokładnie jeden raz wyrzucono orła.
Spośród wszystkich liczb naturalnych sześciocyfrowych, których wszystkie cyfry należą do zbioru 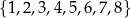 , losujemy jedną. Wylosowanie każdej z tych liczb jest jednakowo prawdopodobne. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę, która ma następującą własność: kolejne cyfry tej liczby (licząc od lewej strony) tworzą – w podanej kolejności – sześciowyrazowy ciąg malejący.
, losujemy jedną. Wylosowanie każdej z tych liczb jest jednakowo prawdopodobne. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę, która ma następującą własność: kolejne cyfry tej liczby (licząc od lewej strony) tworzą – w podanej kolejności – sześciowyrazowy ciąg malejący.
W magazynie są dwie równe partie elementów produkowanych w fabrykach I i II. Niezawodność (w czasie 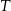 ) elementów z fabryki I jest równa 0,9, a z fabryki II 0,7. W sposób przypadkowy wzięto jeden element z magazynu i okazało się, że był sprawny przez czas
) elementów z fabryki I jest równa 0,9, a z fabryki II 0,7. W sposób przypadkowy wzięto jeden element z magazynu i okazało się, że był sprawny przez czas 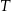 . Obliczyć prawdopodobieństwo, że wybrany element pochodzi z fabryki I.
. Obliczyć prawdopodobieństwo, że wybrany element pochodzi z fabryki I.
Grupa 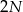 chłopców i
chłopców i 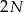 dziewcząt podzieliła się losowo na 2 równoliczne grupy. Jakie jest prawdopodobieństwo, że w każdej z tych grup jest tyle samo chłopców co dziewcząt?
dziewcząt podzieliła się losowo na 2 równoliczne grupy. Jakie jest prawdopodobieństwo, że w każdej z tych grup jest tyle samo chłopców co dziewcząt?
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo każdego z następujących zdarzeń:
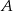 — w każdym rzucie wypadnie nieparzysta liczba oczek.
— w każdym rzucie wypadnie nieparzysta liczba oczek. 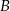 -– suma oczek otrzymanych w obu rzutach jest liczbą większą od 9.
-– suma oczek otrzymanych w obu rzutach jest liczbą większą od 9. 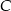 -– suma oczek otrzymanych w obu rzutach jest liczbą nieparzystą i większą od 9.
-– suma oczek otrzymanych w obu rzutach jest liczbą nieparzystą i większą od 9.
W każdej z czterech urn są 24 kule, w tym dokładnie 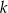 białych. Z każdej urny losujemy jedną kulę. Dla jakiej wartości
białych. Z każdej urny losujemy jedną kulę. Dla jakiej wartości 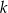 prawdopodobieństwo wylosowania dokładnie dwóch kul białych jest największe? Oblicz to największe prawdopodobieństwo.
prawdopodobieństwo wylosowania dokładnie dwóch kul białych jest największe? Oblicz to największe prawdopodobieństwo.
W pojemniku znajduje się 200 wybrakowanych części. 60 sztuk odrzucono z powodu wystąpienia wady 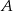 , 40 sztuk z powodu wady
, 40 sztuk z powodu wady 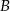 , pozostałe z powodu wady
, pozostałe z powodu wady 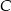 . Każda część ma tylko jedną wadę. Oblicz prawdopodobieństwo, że wybierając losowo z tego pojemnika 3 części, wybierzesz dokładnie po jednej części z każdą z wad.
. Każda część ma tylko jedną wadę. Oblicz prawdopodobieństwo, że wybierając losowo z tego pojemnika 3 części, wybierzesz dokładnie po jednej części z każdą z wad.
W pojemniku znajduje się 200 wybrakowanych części. 60 sztuk odrzucono z powodu wystąpienia wady 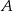 , 40 sztuk z powodu wady
, 40 sztuk z powodu wady 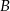 , pozostałe z powodu wady
, pozostałe z powodu wady 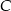 . Każda część ma tylko jedną wadę. Oblicz prawdopodobieństwo, że wybierając losowo z tego pojemnika 3 części, wybierzesz dokładnie dwie części z wadą
. Każda część ma tylko jedną wadę. Oblicz prawdopodobieństwo, że wybierając losowo z tego pojemnika 3 części, wybierzesz dokładnie dwie części z wadą 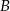 .
.
W pojemniku znajduje się 200 wybrakowanych części. 60 sztuk odrzucono z powodu wystąpienia wady 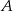 , 40 sztuk z powodu wady
, 40 sztuk z powodu wady 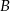 , pozostałe z powodu wady
, pozostałe z powodu wady 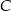 . Każda część ma tylko jedną wadę. Oblicz prawdopodobieństwo, że wybierając losowo z tego pojemnika 3 części, wybierzesz dokładnie dwie części z wadą
. Każda część ma tylko jedną wadę. Oblicz prawdopodobieństwo, że wybierając losowo z tego pojemnika 3 części, wybierzesz dokładnie dwie części z wadą 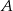 .
.
W pojemniku znajduje się 200 wybrakowanych części. 60 sztuk odrzucono z powodu wystąpienia wady 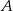 , 40 sztuk z powodu wady
, 40 sztuk z powodu wady 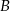 , pozostałe z powodu wady
, pozostałe z powodu wady 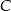 . Każda część ma tylko jedną wadę. Oblicz prawdopodobieństwo, że wybierając losowo z tego pojemnika 3 części, wybierzesz wszystkie części z tą samą jedną wadą.
. Każda część ma tylko jedną wadę. Oblicz prawdopodobieństwo, że wybierając losowo z tego pojemnika 3 części, wybierzesz wszystkie części z tą samą jedną wadą.
W jadalni znajduje się okrągły stół, przy którym może usiąść 6 osób. Pod ścianą stoi ława, na której również może usiąść 6 osób. Do jadalni wchodzi 6 osób, które najpierw w sposób losowy siadają przy stole, a następnie na ławie. Które z prawdopodobieństw jest większe: prawdopodobieństwo tego, że 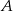 i
i 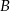 będą sąsiadami, siadając przy stole, czy prawdopodobieństwo tego, że
będą sąsiadami, siadając przy stole, czy prawdopodobieństwo tego, że 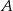 i
i 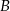 będą sąsiadami, siadając na ławie?
będą sąsiadami, siadając na ławie?
Oblicz prawdopodobieństwo, że w rzucie pięcioma sześciennymi kostkami do gry otrzymamy sumę oczek różną od 28.
Do woreczka wrzucono 3 monety 5 złotowe, 4 monety 2 złotowe, 2 monety 1 złotowe oraz 8 monet 50 groszowych. Karol losowo wyjmuje z woreczka 10 monet. Jakie jest prawdopodobieństwo, że wylosuje w ten sposób co najmniej 10 zł? Wynik podaj z dokładnością do trzech miejsc po przecinku.
Z cyfr 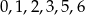 tworzymy liczbę czterocyfrową, przy czym cyfry nie mogą się powtarzać. Jakie jest prawdopodobieństwo otrzymania liczby podzielnej przez 25?
tworzymy liczbę czterocyfrową, przy czym cyfry nie mogą się powtarzać. Jakie jest prawdopodobieństwo otrzymania liczby podzielnej przez 25?
Na jednej kostce sześciennej znajdują się liczby: 2,3,3,6,6,6, a na drugiej: 1,1,4,6,7,7. Gra polega na rzucie wybraną kostką. Wygrywa ten, kto wyrzuci większą liczbę na swojej kostce. Masz prawo wyboru kostki. Którą kostkę należy wybrać, aby mieć większe szanse wygranej?
Zamek szyfrowy składa się z 5 tarcz. Na każdej z tarcz znajduje się 6 cyfr. Zamek otwiera kombinacja cyfr podana w odpowiedniej kolejności. (istotne są cyfry na tarczach oraz kolejność ustawiania tarcz). Jakie jest prawdopodobieństwo otworzenia zamka przy losowym ustawieniu tarcz?
Ze zbioru 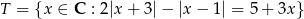 losujemy 3 liczby
losujemy 3 liczby 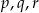 ze zwracaniem i tworzymy funkcję
ze zwracaniem i tworzymy funkcję 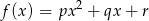 . Oblicz prawdopodobieństwa zdarzeń:
. Oblicz prawdopodobieństwa zdarzeń:
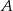 – otrzymana funkcja jest parzysta.
– otrzymana funkcja jest parzysta. 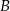 – otrzymana funkcja jest różnowartościowa.
– otrzymana funkcja jest różnowartościowa. 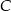 – otrzymana funkcja jest stała.
– otrzymana funkcja jest stała.
Ze zbioru 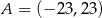 losujemy dwucyfrową liczbę całkowitą
losujemy dwucyfrową liczbę całkowitą  , natomiast ze zbioru
, natomiast ze zbioru 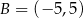 losujemy liczbę całkowitą
losujemy liczbę całkowitą 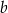 . Te liczby są współczynnikami funkcji
. Te liczby są współczynnikami funkcji 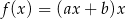 . Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wykres otrzymanej funkcji
. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wykres otrzymanej funkcji 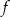 ma co najmniej dwa punkty wspólne z prostą
ma co najmniej dwa punkty wspólne z prostą 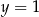 .
.
W jednej szufladzie znajdują się 3 szaliki czarne i 4 szaliki niebieskie, a w drugiej szufladzie są 2 czapki czarne i 1 niebieska. Wyjmujemy losowo jeden szalik i jedną czapkę. Które prawdopodobieństwo jest większe: zdarzenia 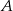 , że otrzymamy komplet w jednym kolorze, czy zdarzenia
, że otrzymamy komplet w jednym kolorze, czy zdarzenia 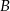 , że otrzymamy czapkę i szalik w różnych kolorach? Odpowiedź uzasadnij, wykonując odpowiednie obliczenia.
, że otrzymamy czapkę i szalik w różnych kolorach? Odpowiedź uzasadnij, wykonując odpowiednie obliczenia.
W każdym z dwóch koszyków znajduje się 5 klocków czerwonych, 10 zielonych i 6 białych. Wyjmujemy losowo po jednym klocku z każdego koszyka. Oblicz prawdopodobieństwo, że:
- wylosujemy dwa klocki białe;
- wylosujemy klocki tego samego koloru.
Ze zbioru liczb 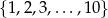 losujemy bez zwracania dwie i od pierwszej odejmujemy drugą. Oblicz prawdopodobieństwo, że otrzymana różnica jest większa od 2.
losujemy bez zwracania dwie i od pierwszej odejmujemy drugą. Oblicz prawdopodobieństwo, że otrzymana różnica jest większa od 2.
Ze zbioru liczb 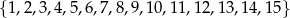 losujemy bez zwracania dwa razy po jednej liczbie. Wylosowane liczby tworzą parę
losujemy bez zwracania dwa razy po jednej liczbie. Wylosowane liczby tworzą parę 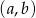 , gdzie
, gdzie  jest wynikiem pierwszego losowania,
jest wynikiem pierwszego losowania, 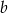 jest wynikiem drugiego losowania. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn
jest wynikiem drugiego losowania. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn 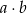 jest liczbą parzystą.
jest liczbą parzystą.
Rzucono dwiema sześciennymi kostkami do gry i określono zdarzenia: 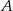 – na każdej kostce wypadła inna liczba oczek,
– na każdej kostce wypadła inna liczba oczek, 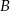 – suma oczek jest mniejsza od 6. Oblicz prawdopodobieństwo zdarzenia
– suma oczek jest mniejsza od 6. Oblicz prawdopodobieństwo zdarzenia 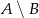 .
.

