Z definicji/Prawdopodobieństwo - zadania z matematyki

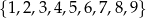Ze zbioru {1,2,3,4,5,6,7 ,8 ,9} losujemy kolejno ze zwracaniem trzy liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie spośród trzech wylosowanych liczb będą równe. Wynik zapisz w postaci ułamka nieskracalnego.

Danych jest 5 pudełek ponumerowanych liczbami od 1 do 5. W każdym pudełku znajduje się 20 kul ponumerowanych liczbami od 1 do 20. Z każdego pudełka wybieramy jedną kulę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że każda z wylosowanych liczb jest mniejsza od wszystkich liczb wylosowanych z pudełek o większych numerach. Wynik podaj w postaci ułamka nieskracalnego.

Do 12 ponumerowanych szuﬂad wkładamy losowo 13 pojedynczych skarpetek, przy czym dokładnie dwie z nich tworzą parę. Jakie jest prawdopodobieństwo otrzymania konﬁguracji, w której żadna szuﬂada nie jest pusta oraz skarpetki tworzące parę znajdują się w różnych szuﬂadach.

Strzelając do tarczy pewien strzelec uzyskuje co najmniej 9 punktów z prawdopodobieństwem 0,5, a co najwyżej 9 punktów z prawdopodobieństwem 0,7. Oblicz prawdopodobieństwo, że ten strzelec uzyska dokładnie 9 punktów.

Oblicz prawdopodobieństwo, że w dziesięciu rzutach kostką dokładnie na dwóch kostkach otrzymamy ściankę z dwoma oczkami i dokładnie na trzech kostkach ściankę z trzema oczkami.

Rzucamy sześcienną kostką i monetą. Jakie jest prawdopodobieństwo, że na monecie wypadnie reszka, a na kostce nie więcej niż 4 oczka.

Liczby kul białych, niebieskich i czerwonych tworzą - w podanej kolejności - ciąg arytmetyczny o różnicy 2. Spośród tych kul losujemy jednocześnie trzy. Prawdopodobieństwo wylosowania trzech kul, z których każda jest innego koloru wynosi 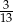3- 13 . Oblicz prawdopodobieństwo wylosowania z tej urny trzech kul, wśród których dwie są tego samego koloru, jeśli wiadomo, że liczba wszystkich kul w urnie jest nieparzysta.

Grupę siedmiu osób, w których są trzy dziewczynki i czterech chłopców ustawiamy w rzędzie jeden za drugim. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że żadne dwie dziewczynki nie stoją bezpośrednio za sobą.

Oblicz prawdopodobieństwo, że w trzech rzutach symetryczną sześcienną kostką do gry suma kwadratów liczb wyrzuconych oczek będzie podzielna przez 4.

10 kul rozmieszczamy w 10 szuﬂadach. Jakie jest prawdopodobieństwo tego, że każda szuﬂada będzie zajęta?

Liczba uczniów w klasie jest 812 razy mniejsza od liczby utworzonych z nich uporządkowanych trójek. Oblicz prawdopodobieństwo wylosowania trzech osób, które (w kolejności losowania) są zapisane w dzienniku pod numerami pierwszym, drugim, i trzecim.

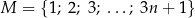Niech będzie ustaloną liczbą naturalną dodatnią. Ze zbioru M = {1; 2; 3; ...; 3n+ 1} losujemy jednocześnie trzy liczby. Zdarzenie 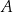odpowiada jednoczesnemu wylosowaniu ze zbioru 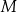trzech liczb, których suma przy dzieleniu przez 3 daje resztę 1. Oblicz prawdopodobieństwo zdarzenia .

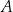Ze zbioru 99 kolejnych liczb naturalnych – od 1 do 99 – losujemy kolejno bez zwracania dwa razy po jednej liczbie. Niech 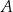oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest liczbą parzystą. Oblicz prawdopodobieństwo zdarzenia .

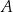Rzucamy dwiema sześciennymi kostkami.

Jakie jest prawdopodobieństwo, że różnica między liczbami oczek wyrzuconych na kostkach (od większej odejmujemy mniejszą) będzie równa 2?
Jaka jest najbardziej prawdopodobna różnica między wynikami na kostkach (od większego odejmujemy mniejszy)?

Rzucamy trzema kostkami. Prawdopodobieństwo otrzymania sumy oczek równej 3 wynosi 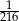1216- , a prawdopodobieństwo otrzymania sumy oczek równej 4 wynosi 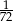-1 72 . jakie jest prawdopodobieństwo tego, że suma otrzymanych oczek będzie mniejsza od 5?

Na loterię przygotowano 30 losów, z których jest wygrywających. Kupujemy 2 razy po jednym losie. Wyznacz , jeśli wiadomo, że prawdopodobieństwo kupienia w ten sposób dwóch losów wygrywających jest równe 219 .

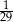Przy okrągłym stole zasiada losowo 8 osób, a wśród nich rodzice z dwojgiem dzieci. Jakie jest prawdopodobieństwo tego, że dzieci usiądą bezpośrednio między rodzicami?

Rzucamy cztery razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn liczb oczek otrzymanych we wszystkich czterech rzutach będzie równy 60 .

W pewnej grupie uczniów każdy zna język angielski lub niemiecki. Wiadomo, że prawdopodobieństwo wylosowania z tej grupy ucznia znającego język angielski jest równe , natomiast prawdopodobieństwo wylosowania ucznia znającego język niemiecki jest równe 4 5 . Jakie jest prawdopodobieństwo tego, że losowo wybrany uczeń zna obydwa języki?

Z talii 52 kart wyciągamy losowo jedną. Oblicz prawdopodobieństwo, że wyciągnięta karta będzie damą lub treﬂem.

Największy internetowy zbiór zadań z matematyki

/Szkoła średnia/Prawdopodobieństwo/Z definicji