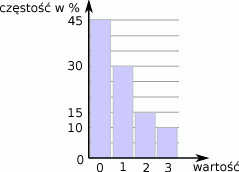
Oblicz średnią arytmetyczną danych przedstawionych na poniższym diagramie częstości
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz średnią arytmetyczną danych przedstawionych na poniższym diagramie częstości

Marek waha się, który obóz letni wybrać. Aby podjąć najlepszą decyzję sporządził tabelkę i obliczył średnie ważone. Który obóz powinien wybrać?
| Koszt (waga 0,4) | Termin (waga 0,1) | Towarzystwo (waga 0,3) | Atrakcyjność (waga 0,2) | Średnia | |
| Obóz wędkarski | 8 | 2 | 8 | 4 | |
| Obóz żeglarski | 4 | 4 | 6 | 7 | |
| Obóz rowerowy | 7 | 6 | 5 | 5 |
Tabela przedstawia wyniki części teoretycznej egzaminu na prawo jazdy. Zdający uzyskał wynik pozytywny, jeżeli popełnił co najwyżej dwa błędy.
| Liczba błędów | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Liczba zdających | 8 | 5 | 8 | 5 | 2 | 1 | 0 | 0 | 1 |
Na wykresie słupkowym poniżej podano rozkład miesięcznych zarobków wszystkich pracowników w pewnej firmie 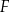 . Na osi poziomej podano – wyrażone w tysiącach złotych – miesięczne wynagrodzenie netto pracowników firmy
. Na osi poziomej podano – wyrażone w tysiącach złotych – miesięczne wynagrodzenie netto pracowników firmy 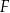 , a na osi pionowej przedstawiono liczbę osób, która osiąga podane zarobki.
, a na osi pionowej przedstawiono liczbę osób, która osiąga podane zarobki.
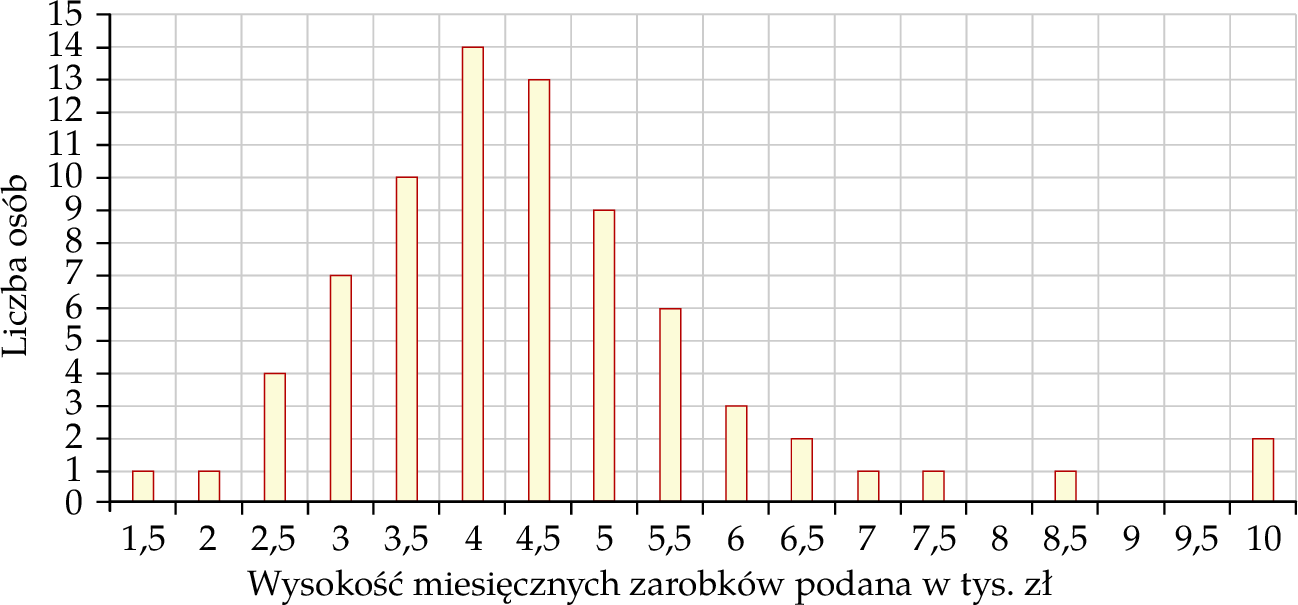
Oblicz średnią miesięcznego wynagrodzenia netto wszystkich pracowników firmy 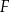 .
.
Na wykresie słupkowym poniżej podano rozkład miesięcznych zarobków wszystkich pracowników w pewnej firmie 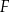 . Na osi poziomej podano – wyrażone w tysiącach złotych – miesięczne wynagrodzenie netto pracowników firmy
. Na osi poziomej podano – wyrażone w tysiącach złotych – miesięczne wynagrodzenie netto pracowników firmy 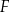 , a na osi pionowej przedstawiono liczbę osób, która osiąga podane zarobki.
, a na osi pionowej przedstawiono liczbę osób, która osiąga podane zarobki.
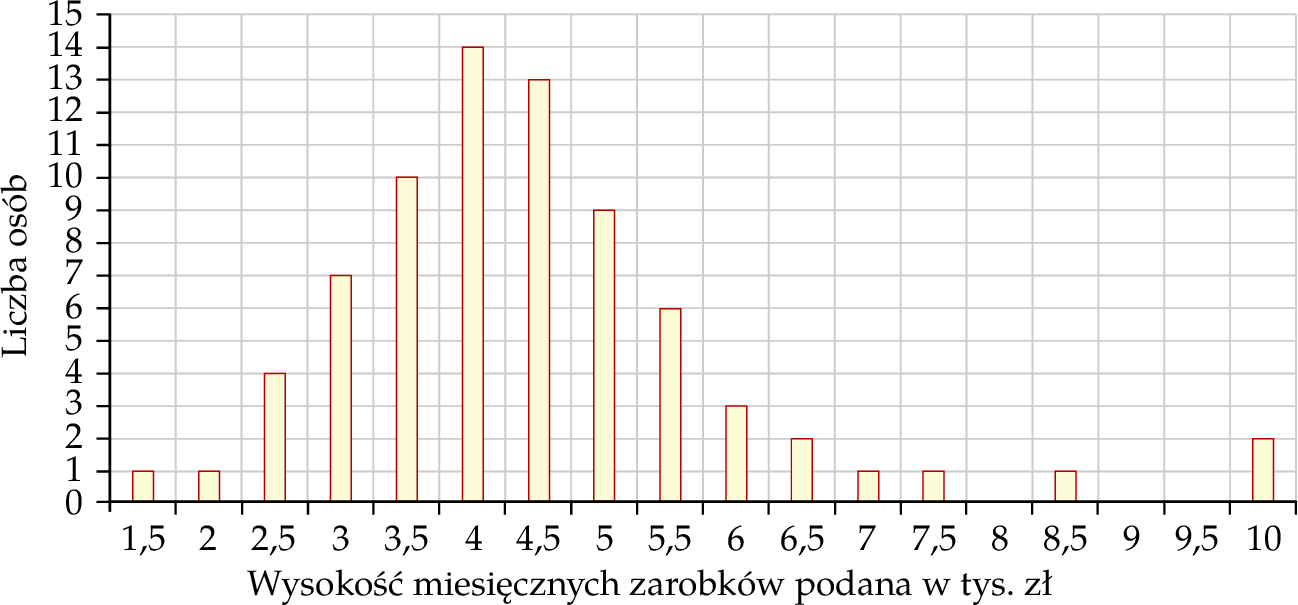
Oblicz medianę miesięcznych zarobków w firmie 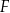 .
.
Tabela przedstawia dane dotyczące wieku kobiet i mężczyzn pracujących w małej firmie zatrudniającej 7 osób:
| Kobiety | Mężczyźni | |
| Liczba osób | 3 | 4 |
| Średni wiek | 26 | 33 |
| Odchylenie standardowe | 1,4 | 4,6 |
Wyznacz średnie odchylenie standardowe liczone dla wszystkich osób pracujących w tej firmie.
Kwadrat odchylenia standardowego danych: 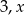 jest równy 1. Oblicz
jest równy 1. Oblicz  .
.
Mediana trzech liczb jest równa 4, a ich średnia arytmetyczna jest równa 5. Oblicz sumę największej i najmniejszej z tych liczb.
W eksperymencie badano kiełkowanie nasion w pięciu donicach. Na koniec eksperymentu policzono wykiełkowane nasiona w każdej z donic:
– w I donicy – 113 nasiona
– w II donicy – 141 nasion
– w III donicy – 99 nasion
– w IV donicy – 127 nasion
– w V donicy – 120 nasion.
Oblicz odchylenie standardowe liczby wykiełkowanych nasion.
Pewna maszyna wykonuje śruby o średnicy 14 mm. Dokonano kontroli jakości wykonywanych śrub i jej wyniki zebrano w tabeli.
| Średnica w mm | 13,8 | 13,9 | 14 | 14,1 | 14,2 |
| Liczba śrub | 8 | 17 | 48 | 13 | 14 |
Opierając się na podanych danych.
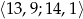 .
. Do szkolnego koła czytelniczego należy 50 uczniów. Opiekun koła zebrał dane dotyczące liczby książek przeczytanych przez tych uczniów w listopadzie 2024 roku. W poniższej tabeli przedstawiono wyniki zebrane przez opiekuna.
| Liczba przeczytanych książek | 4 | 5 | 6 | 7 | 8 |
| Liczba uczniów, którzy przeczytali daną liczbę książek | 5 | 8 | 12 | 13 | 12 |
Oblicz średnią arytmetyczną liczby przeczytanych książek w tej grupie uczniów.
Oblicz medianę liczby przeczytanych książek w tej grupie uczniów.
Średnia arytmetyczna dwóch liczb wynosi 20. Jeśli jedną z nich zwiększymy dwukrotnie, a drugą zmniejszymy o 50%, to średnia arytmetyczna zwiększy się o 2. Wyznacz te liczby.
Średnia arytmetyczna dwóch liczb wynosi 16. Jeśli jedną z nich zmniejszymy dwukrotnie, a drugą zwiększymy o 50%, to średnia arytmetyczna zwiększy się o 2. Wyznacz te liczby.
Średnia arytmetyczna liczb 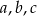 jest równa 15. Oblicz średnią arytmetyczną liczb
jest równa 15. Oblicz średnią arytmetyczną liczb 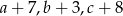 .
.
W pewnym zakładzie pracy obliczono ile dni urlopu wykorzystali pracownicy w lutym. Wynik przedstawiono w następującym diagramie słupkowym
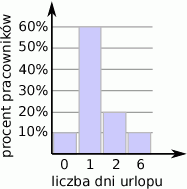
Sprzedawca kwiatów notował w tabeli ilość otrzymanych banknotów z podziałem według ich nominałów.
| 1 dzień | 2 dzień | 3 dzień | 4 dzień | 5 dzień | |
| 10 zł | 2 | 7 | 4 | 6 | 1 |
| 20 zł | 5 | 5 | 2 | 4 | 3 |
| 50 zł | 2 | 3 | 0 | 3 | 5 |
| 100 zł | 1 | 3 | 1 | 1 | 2 |
W tabeli przedstawiono informację o długości stóp uczniów klasy IIIc.
| liczba uczniów | 1 | 3 | 2 | 4 | 3 | 5 | 3 | 4 |
| długość stopy (w cm) | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 |
Oblicz średnią długość stopy ucznia tej klasy. Otrzymany wynik zaokrąglij do 1 cm. Oblicz błąd względny otrzymanego przybliżenia.
W tabeli zestawiono oceny z matematyki uczniów klasy 3A na koniec semestru.
| Ocena | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba ocen | 0 | 4 | 9 | 13 |  | 1 |
Średnia arytmetyczna tych ocen jest równa 3,6. Oblicz liczbę  ocen bardzo dobrych (5) z matematyki wystawionych na koniec semestru w tej klasie.
ocen bardzo dobrych (5) z matematyki wystawionych na koniec semestru w tej klasie.
W tabeli przedstawiono oceny ze sprawdzianu z matematyki w klasie 1B.
| Ocena | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba ocen | 3 | 3 | 6 |  | 4 | 2 |
Średnia arytmetyczna tych ocen jest równa 3,48. Oblicz liczbę  ocen dobrych (4) otrzymanych przez uczniów na tym sprawdzianie.
ocen dobrych (4) otrzymanych przez uczniów na tym sprawdzianie.
Oblicz z dokładnością do 0,1 odchylenie standardowe następujących danych:
| Wartość | -3 | -1 | 0 | 4 | 6 |
| Liczebność | 10 | 6 | 4 | 2 | 3 |
Oblicz medianę następujących danych: 13,2; 15; 12,225; 14; 16,8; 42,7; 22,1; 31,4; 20,6; 18,4.
Oblicz medianę danych przedstawionych w postaci tabeli liczebności
| Wartość | 0 | 1 | 2 | 3 |
| Liczebność | 4 | 3 | 1 | 1 |
Oblicz medianę następujących danych:
| Wartość | 0,2 | 1 | 1,4 | 2 | 2,5 | 3 |
| Liczebność | 2 | 1 | 2 | 2 | 3 | 12 |
