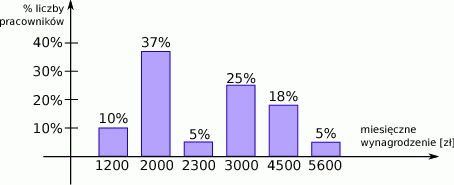
Przeprowadzono badania, dotyczące liczby osób jadących w samochodach osobowych w godzinach rannych, w kierunku centrum pewnego miasta. Wyniki badań przedstawione są na digramie kołowym.

- Oblicz średnią liczbę osób jadących w samochodzie osobowym w godzinach rannych w kierunku centrum.
- Oblicz prawdopodobieństwo, że w losowo wybranym samochodzie osobowym, w godzinach rannych, w kierunku centrum, były więcej niż 3 osoby.
- Wiedząc, że samochodów osobowych, w których były 4 osoby, zaobserwowano o 350 więcej, niż samochodów w których było 5 osób, oblicz, ile wszystkich samochodów obserwowano w trakcie badań.

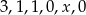 jest równa 2. Oblicz
jest równa 2. Oblicz  .
. 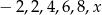 jest równa 5. Wyznacz liczbę
jest równa 5. Wyznacz liczbę  .
. 
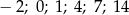 .
. 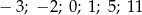 .
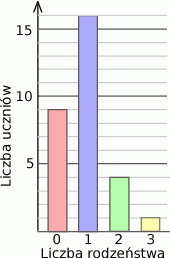
. 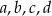 jest równe 0,1. Oblicz odchylenie standardowe danych:
jest równe 0,1. Oblicz odchylenie standardowe danych: 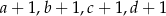 .
. 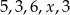 . Średnia arytmetyczna tych ocen jest równa 4. Oblicz
. Średnia arytmetyczna tych ocen jest równa 4. Oblicz  i medianę tych pięciu ocen.
i medianę tych pięciu ocen. 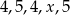 . Średnia arytmetyczna tych ocen jest równa 4,4. Oblicz
. Średnia arytmetyczna tych ocen jest równa 4,4. Oblicz  i medianę tych pięciu ocen.
i medianę tych pięciu ocen. 
 .
. 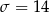 . Podaj numery donic, w których liczba wykiełkowanych nasion mieści się w przedziale określonym przez jedno odchylenie standardowe od średniej.
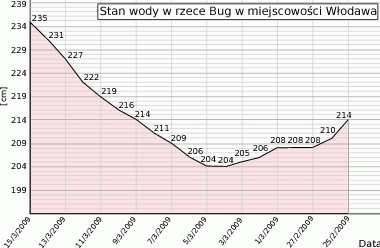
. Podaj numery donic, w których liczba wykiełkowanych nasion mieści się w przedziale określonym przez jedno odchylenie standardowe od średniej. 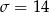 . Podaj numery kierowców, dla których liczba przejechanych kilometrów mieści się w przedziale określonym przez jedno odchylenie standardowe od średniej.
. Podaj numery kierowców, dla których liczba przejechanych kilometrów mieści się w przedziale określonym przez jedno odchylenie standardowe od średniej. 