Spośród liczb 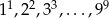 wybieramy losowo trzy. Oblicz prawdopodobieństwo, że iloczyn tych liczb jest parzysty.
wybieramy losowo trzy. Oblicz prawdopodobieństwo, że iloczyn tych liczb jest parzysty.
/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb
Ze zbioru 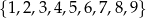 losujemy kolejno ze zwracaniem trzy liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie spośród trzech wylosowanych liczb będą równe. Wynik zapisz w postaci ułamka nieskracalnego.
losujemy kolejno ze zwracaniem trzy liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwie spośród trzech wylosowanych liczb będą równe. Wynik zapisz w postaci ułamka nieskracalnego.
Niech  będzie ustaloną liczbą naturalną dodatnią. Ze zbioru
będzie ustaloną liczbą naturalną dodatnią. Ze zbioru 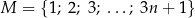 losujemy jednocześnie trzy liczby. Zdarzenie
losujemy jednocześnie trzy liczby. Zdarzenie 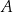 odpowiada jednoczesnemu wylosowaniu ze zbioru
odpowiada jednoczesnemu wylosowaniu ze zbioru 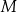 trzech liczb, których suma przy dzieleniu przez 3 daje resztę 1. Oblicz prawdopodobieństwo zdarzenia
trzech liczb, których suma przy dzieleniu przez 3 daje resztę 1. Oblicz prawdopodobieństwo zdarzenia 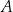 .
.
Ze zbioru 99 kolejnych liczb naturalnych – od 1 do 99 – losujemy kolejno bez zwracania dwa razy po jednej liczbie. Niech 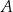 oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest liczbą parzystą. Oblicz prawdopodobieństwo zdarzenia
oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest liczbą parzystą. Oblicz prawdopodobieństwo zdarzenia 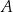 .
.
Spośród wszystkich liczb naturalnych sześciocyfrowych, których wszystkie cyfry należą do zbioru 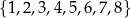 , losujemy jedną. Wylosowanie każdej z tych liczb jest jednakowo prawdopodobne. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę, która ma następującą własność: kolejne cyfry tej liczby (licząc od lewej strony) tworzą – w podanej kolejności – sześciowyrazowy ciąg malejący.
, losujemy jedną. Wylosowanie każdej z tych liczb jest jednakowo prawdopodobne. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę, która ma następującą własność: kolejne cyfry tej liczby (licząc od lewej strony) tworzą – w podanej kolejności – sześciowyrazowy ciąg malejący.
Z cyfr 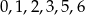 tworzymy liczbę czterocyfrową, przy czym cyfry nie mogą się powtarzać. Jakie jest prawdopodobieństwo otrzymania liczby podzielnej przez 25?
tworzymy liczbę czterocyfrową, przy czym cyfry nie mogą się powtarzać. Jakie jest prawdopodobieństwo otrzymania liczby podzielnej przez 25?
Zamek szyfrowy składa się z 5 tarcz. Na każdej z tarcz znajduje się 6 cyfr. Zamek otwiera kombinacja cyfr podana w odpowiedniej kolejności. (istotne są cyfry na tarczach oraz kolejność ustawiania tarcz). Jakie jest prawdopodobieństwo otworzenia zamka przy losowym ustawieniu tarcz?
Ze zbioru 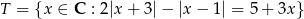 losujemy 3 liczby
losujemy 3 liczby 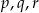 ze zwracaniem i tworzymy funkcję
ze zwracaniem i tworzymy funkcję 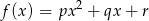 . Oblicz prawdopodobieństwa zdarzeń:
. Oblicz prawdopodobieństwa zdarzeń:
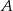 – otrzymana funkcja jest parzysta.
– otrzymana funkcja jest parzysta. 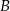 – otrzymana funkcja jest różnowartościowa.
– otrzymana funkcja jest różnowartościowa. 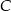 – otrzymana funkcja jest stała.
– otrzymana funkcja jest stała.
Ze zbioru 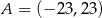 losujemy dwucyfrową liczbę całkowitą
losujemy dwucyfrową liczbę całkowitą  , natomiast ze zbioru
, natomiast ze zbioru 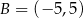 losujemy liczbę całkowitą
losujemy liczbę całkowitą 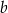 . Te liczby są współczynnikami funkcji
. Te liczby są współczynnikami funkcji 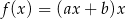 . Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wykres otrzymanej funkcji
. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wykres otrzymanej funkcji 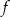 ma co najmniej dwa punkty wspólne z prostą
ma co najmniej dwa punkty wspólne z prostą 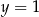 .
.
Ze zbioru liczb 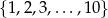 losujemy bez zwracania dwie i od pierwszej odejmujemy drugą. Oblicz prawdopodobieństwo, że otrzymana różnica jest większa od 2.
losujemy bez zwracania dwie i od pierwszej odejmujemy drugą. Oblicz prawdopodobieństwo, że otrzymana różnica jest większa od 2.
Ze zbioru liczb 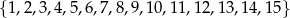 losujemy bez zwracania dwa razy po jednej liczbie. Wylosowane liczby tworzą parę
losujemy bez zwracania dwa razy po jednej liczbie. Wylosowane liczby tworzą parę 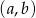 , gdzie
, gdzie  jest wynikiem pierwszego losowania,
jest wynikiem pierwszego losowania, 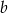 jest wynikiem drugiego losowania. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn
jest wynikiem drugiego losowania. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn 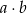 jest liczbą parzystą.
jest liczbą parzystą.
Ze zbioru liczb 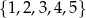 losujemy kolejno trzy razy po jednej liczbie ze zwracaniem tworząc liczbę trzycyfrową. Oblicz prawdopodobieństwo zdarzenia
losujemy kolejno trzy razy po jednej liczbie ze zwracaniem tworząc liczbę trzycyfrową. Oblicz prawdopodobieństwo zdarzenia 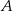 – otrzymana liczba jest cztery razy większa od kwadratu liczby naturalnej.
– otrzymana liczba jest cztery razy większa od kwadratu liczby naturalnej.
Spośród liczb: -9, -7, -5, -3, -1, 0, 2, 4, 6, 8 losujemy dwie różne liczby  i
i 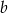 , a następnie zapisujemy ich iloczyn
, a następnie zapisujemy ich iloczyn 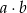 . Oblicz i porównaj prawdopodobieństwa zdarzeń
. Oblicz i porównaj prawdopodobieństwa zdarzeń 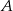 i
i 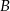 , jeśli:
, jeśli: 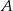 oznacza zdarzenie, że iloczyn
oznacza zdarzenie, że iloczyn 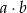 jest liczbą nieujemną;
jest liczbą nieujemną; 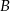 – zdarzenie, że iloczyn
– zdarzenie, że iloczyn 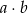 jest liczbą niedodatnią.
jest liczbą niedodatnią.
Ze zbioru 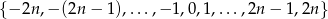 losujemy ze zwracaniem dwie liczby:
losujemy ze zwracaniem dwie liczby:  i
i 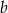 . Rozważmy zdarzenia
. Rozważmy zdarzenia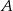 :
: 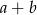 jest liczbą parzystą;
jest liczbą parzystą;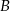 :
: 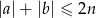 .
.
Oblicz prawdopodobieństwo zdarzenia 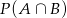 .
.
Dany jest zbiór 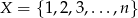 ,
, 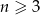 ,
, 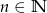 . Ze zbioru
. Ze zbioru 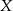 losujemy kolejno bez zwracania dwie liczby. Oblicz prawdopodobieństwo, że pierwsza z wylosowanych liczb jest większa od drugiej.
losujemy kolejno bez zwracania dwie liczby. Oblicz prawdopodobieństwo, że pierwsza z wylosowanych liczb jest większa od drugiej.
Ze zbioru 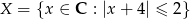 losujemy dwa razy (bez zwracania) po jednej liczbie. Oznaczamy te liczby w kolejności losowania przez
losujemy dwa razy (bez zwracania) po jednej liczbie. Oznaczamy te liczby w kolejności losowania przez  oraz
oraz 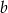 . Oblicz prawdopodobieństwo tego, że wylosowana para liczb
. Oblicz prawdopodobieństwo tego, że wylosowana para liczb 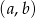 jest rozwiązaniem nierówności
jest rozwiązaniem nierówności 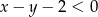 .
.
Ze zbioru wszystkich trójwyrazowych ciągów o wyrazach ze zbioru 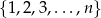 losujemy jeden ciąg.
losujemy jeden ciąg.
- Oblicz prawdopodobieństwo wylosowania ciągu rosnącego lub malejącego.
- Dla jakiej liczby naturalnej
 prawdopodobieństwo to jest równe 0,125?
prawdopodobieństwo to jest równe 0,125?
Liczby 1, 2, 3, 4, 5, 6, 7, 8 ustawiamy losowo w szeregu. Oblicz prawdopodobieństwo, że w tym ustawieniu suma każdych dwóch sąsiednich liczb będzie nieparzysta. Wynik podaj w postaci ułamka nieskracalnego.
Losujemy jedną liczbę spośród liczb: 1, 2, 3,…, 1000. Oblicz prawdopodobieństwo wylosowania liczby podzielnej przez 4 lub przez 9.
Spośród liczb: 0, 1, 2, 3, 4, 5,…, 1000 wybieramy losowo jedną liczbę. Oblicz prawdopodobieństwo zdarzenia, że liczba ta jest podzielna przez 4 lub 5.
Ze zbioru liczb trzycyfrowych mniejszych od 500 wybieramy losowo jedną liczbę. Jakie jest prawdopodobieństwo, że będzie to liczba podzielna przez 3 lub przez 5?
Ze zbioru 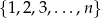 losujemy bez zwracania parę liczb
losujemy bez zwracania parę liczb 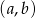 . Dla jakich
. Dla jakich  prawdopodobieństwo wylosowania pary spełniającej warunek
prawdopodobieństwo wylosowania pary spełniającej warunek 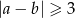 jest większe od
jest większe od 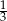 ?
?

