Wielokąt wypukły ma  wierzchołków,
wierzchołków, 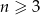 ,
, 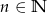 , spośród których losujemy jednocześnie dwa. Wyznacz
, spośród których losujemy jednocześnie dwa. Wyznacz  , wiedząc, że prawdopodobieństwo wylosowania wierzchołków wyznaczających przekątną tego wielokąta jest mniejsze od
, wiedząc, że prawdopodobieństwo wylosowania wierzchołków wyznaczających przekątną tego wielokąta jest mniejsze od 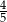 .
.
/Konkursy/Zadania/Kombinatoryka
Grupa szachistów postanowiła zorganizować turniej szachowy w systemie każdy z każdym. Rozgrywano 5 partii dziennie. Turniej trwał 9 dni. Ilu szachistów brało w nim udział ?
Ile jest liczb dziewięciocyfrowych, w których suma każdych trzech kolejnych cyfr jest równa 10?
Na ile sposobów można zapłacić 250 zł monetami 1,2 i 5 złotowymi?
Na niektórych polach szachownicy rozmiaru 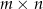 ustawiono wieże. Wiadomo, że dowolna wieża znajduje się w polu rażenia co najwyżej dwóch innych wież. Wyznaczyć, w zależności od
ustawiono wieże. Wiadomo, że dowolna wieża znajduje się w polu rażenia co najwyżej dwóch innych wież. Wyznaczyć, w zależności od 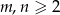 , największą liczbę wież na szachownicy, dla której taka sytuacja jest możliwa.
, największą liczbę wież na szachownicy, dla której taka sytuacja jest możliwa.
Okrąg podzielono dwudziestoma punktami na dwadzieścia łuków tej samej długości. Ile można zbudować łamanych zamkniętych z wierzchołkami w tych punktach i z odcinkami równej długości? (Odcinki mogą się przecinać, ale nie mogą się pokrywać.)
Turnieju tenisowego rozgrywanego systemem każdy z każdym nie ukończyło dwóch graczy. Jeden z nich rozegrał tylko jeden mecz, a drugi dziesięć meczy. Ilu zawodników przystąpiło do turnieju, jeżeli wiadomo, że rozegrano 55 meczy? Czy zawodnicy, którzy nie ukończyli turnieju rozegrali ze sobą mecz?
Uzasadnić, że  prostych może podzielić płaszczyznę na maksymalnie
prostych może podzielić płaszczyznę na maksymalnie 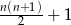 obszarów.
obszarów.

