Punkt 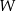 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 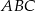 . Prosta przechodząca przez punkty
. Prosta przechodząca przez punkty 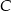 i
i 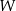 przecina okrąg opisany na trójkącie
przecina okrąg opisany na trójkącie 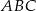 w punkcie
w punkcie 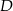 . Wykaż, że trójkąt
. Wykaż, że trójkąt 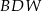 jest równoramienny.
jest równoramienny.
/Konkursy/Zadania/Geometria/Planimetria
Czworokąt 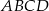 jest trapezem prostokątnym, w którym
jest trapezem prostokątnym, w którym 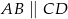 . Wykaż że
. Wykaż że
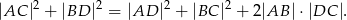
Przez wierzchołek kąta prostego trójkąta prostokątnego o przyprostokątnych 5 i 12 poprowadzono prostą, która dzieli ten trójkąt na dwa trójkąty o równych obwodach. Znajdź stosunek promieni okręgów wpisanych w otrzymane z podziału trójkąty.
Przez wierzchołek kąta prostego trójkąta prostokątnego o przyprostokątnych 8 i 15 poprowadzono prostą, która dzieli ten trójkąt na dwa trójkąty o równych obwodach. Znajdź stosunek promieni okręgów wpisanych w otrzymane z podziału trójkąty.
Oblicz jakie długości powinny mieć boki prostokąta o polu równym 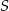 , aby jego przekątna miała najmniejszą możliwą długość. Oblicz długość tej przekątnej.
, aby jego przekątna miała najmniejszą możliwą długość. Oblicz długość tej przekątnej.
Wykaż, że jeżeli kąty wewnętrzne trójkąta spełniają warunek 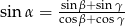 to trójkąt ten jest prostokątny.
to trójkąt ten jest prostokątny.
Na bokach 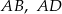 i
i 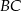 rombu
rombu 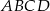 wybrano odpowiednio punkty
wybrano odpowiednio punkty 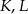 i
i 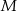 w ten sposób, że odcinki
w ten sposób, że odcinki 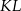 i
i 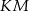 są równoległe do przekątnych rombu. Wykaż, że odcinek
są równoległe do przekątnych rombu. Wykaż, że odcinek 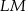 przechodzi przez punkt przecięcia przekątnych rombu.
przechodzi przez punkt przecięcia przekątnych rombu.
Długości podstaw trapezu równoramiennego są równe  oraz
oraz 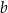 , przy czym
, przy czym 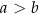 . W ten trapez można wpisać okrąg. Wykaż, że pole tego trapezu jest większe od
. W ten trapez można wpisać okrąg. Wykaż, że pole tego trapezu jest większe od 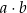 .
.
W trapez 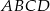 , gdzie
, gdzie 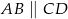 i
i 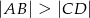 , wpisano okrąg (patrz rysunek).
, wpisano okrąg (patrz rysunek).
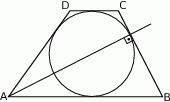
Dwusieczna kąta ostrego przy wierzchołku 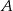 jest prostopadła do ramienia
jest prostopadła do ramienia 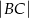 .
.
- Wykaż, że dwusieczna kąta przy wierzchołku
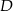 jest równoległa do ramienia
jest równoległa do ramienia 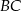 .
. - Oblicz
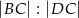 .
.
Podstawy trapezu mają długości 10 i 6. Wiedząc, że suma miar kątów wewnętrznych przy dłuższej podstawie jest równa 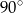 , oblicz długość odcinka łączącego środki podstaw trapezu.
, oblicz długość odcinka łączącego środki podstaw trapezu.
Podstawy trapezu 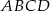 mają długości
mają długości 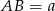 i
i 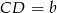 . Na ramionach trapezu wybrano punkty
. Na ramionach trapezu wybrano punkty 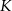 i
i 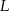 w ten sposób, że odcinek
w ten sposób, że odcinek 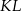 jest równoległy do podstaw i dzieli trapez na dwa trapezy o równych polach. Oblicz długość odcinka
jest równoległy do podstaw i dzieli trapez na dwa trapezy o równych polach. Oblicz długość odcinka 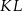 .
.
Dany jest taki czworokąt wypukły 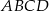 , że okręgi wpisane w trójkąty
, że okręgi wpisane w trójkąty 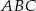 i
i 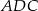 są styczne. Wykaż, że w czworokąt
są styczne. Wykaż, że w czworokąt 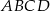 można wpisać okrąg.
można wpisać okrąg.
W okrąg wpisany jest trójkąt 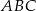 , przy czym
, przy czym 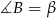 i
i 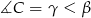 . Oblicz miarę kąta między prostą
. Oblicz miarę kąta między prostą 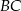 i styczną do okręgu w punkcie
i styczną do okręgu w punkcie 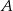 .
.
Trójkąt prostokątny 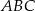 ma boki długości 3, 4, 5. Oblicz promień okręgu stycznego do przeciwprostokątnej i prostych będących przedłużeniami przyprostokątnych.
ma boki długości 3, 4, 5. Oblicz promień okręgu stycznego do przeciwprostokątnej i prostych będących przedłużeniami przyprostokątnych.
Udowodnij, że w czworokącie wpisanym w okrąg suma iloczynów długości przeciwległych boków jest równa iloczynowi długości przekątnych (twierdzenie Ptolemeusza).
Czworokąt 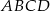 jest trapezem o podstawach
jest trapezem o podstawach 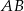 i
i 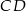 . Wykaż że
. Wykaż że
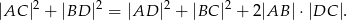
Jedna z podstaw trapezu wpisanego w okrąg jest średnicą okręgu. Oblicz cosinus kąta ostrego trapezu wiedząc, że stosunek obwodu trapezu do sumy długości jego podstaw wynosi 3:2.
Kąt ostry rombu 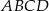 ma miarę
ma miarę 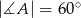 . Na bokach
. Na bokach 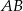 i
i 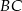 wybrano punkty
wybrano punkty 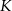 i
i 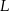 w ten sposób, że
w ten sposób, że 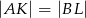 . Uzasadnij, że trójkąt
. Uzasadnij, że trójkąt 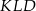 jest trójkątem równobocznym.
jest trójkątem równobocznym.
Wykaż, że proste przechodzące przez wierzchołek równoległoboku i środki boków, do których on nie należy, dzielą przekątną równoległoboku na trzy równe części.
Wykaż, że w dowolnym równoległoboku suma kwadratów długości przekątnych jest równa sumie kwadratów długości wszystkich boków.
Udowodnij że jeśli dwie dwusieczne w trójkącie są sobie równe to trójkąt jest równoramienny (twierdzenie Steinera-Lehmusa).

