W trójkącie równoramiennym 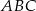 (
(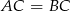 ) poprowadzono wysokości
) poprowadzono wysokości 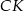 i
i 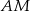 . Wiedząc że
. Wiedząc że 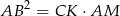 wyznacz cosinus kąta przy podstawie trójkąta.
wyznacz cosinus kąta przy podstawie trójkąta.
/Konkursy/Zadania/Geometria/Planimetria/Trójkąt/Kąty w trójkącie
Wykaż, że istnieją dokładnie dwie liczby naturalne  takie, że trójkąt o bokach
takie, że trójkąt o bokach 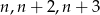 jest rozwartokątny.
jest rozwartokątny.
Środkowa 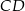 trójkąta
trójkąta 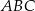 jest równa bokowi
jest równa bokowi 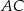 . Wyznacz kąty trójkąta
. Wyznacz kąty trójkąta 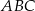 wiedząc, że
wiedząc, że 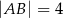 i
i 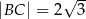 .
.
Wyznacz miary kątów trójkąta, w którym wysokość i środkowa poprowadzona z jednego wierzchołka dzielą kąt przy tym wierzchołku na 3 równe części.
Trójkąty 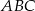 i
i 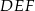 wpisano w ten sam okrąg. Udowodnij, że równość obwodów tych trójkątów jest równoważna równości sum sinusów ich kątów wewnętrznych.
wpisano w ten sam okrąg. Udowodnij, że równość obwodów tych trójkątów jest równoważna równości sum sinusów ich kątów wewnętrznych.
W trójkącie równoramiennym 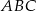 , w którym
, w którym 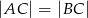 wysokość
wysokość 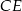 jest dwa razy dłuższa od wysokości
jest dwa razy dłuższa od wysokości 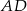 (patrz rysunek). Oblicz kosinusy wszystkich kątów wewnętrznych trójkąta
(patrz rysunek). Oblicz kosinusy wszystkich kątów wewnętrznych trójkąta 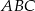 .
.
W trójkącie ostrokątnym 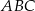 prawdziwa jest równość
prawdziwa jest równość 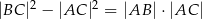 . Wykaż, że kąt
. Wykaż, że kąt 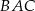 jest dwa razy większy od kąta
jest dwa razy większy od kąta 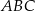 .
.
Wykaż, że jeżeli 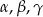 są kątami trójkąta, to
są kątami trójkąta, to
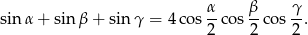
Wyznacz długości boków trójkąta wiedząc, że są one kolejnymi liczbami naturalnymi zaś największy kąt jest dwa razy większy od kąta najmniejszego.
Wykaż, że jeżeli 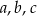 są długościami boków trójkąta leżącymi naprzeciwko odpowiednio kątów o miarach
są długościami boków trójkąta leżącymi naprzeciwko odpowiednio kątów o miarach 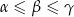 to
to 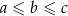 .
.
W trójkącie 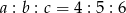 . Wykaż, że w tym trójkącie
. Wykaż, że w tym trójkącie 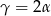 .
.
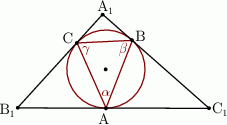
Boki trójkąta 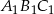 są styczne do okręgu w punktach
są styczne do okręgu w punktach 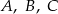 , a kąty trójkąta
, a kąty trójkąta 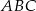 są odpowiednio równe
są odpowiednio równe 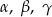 . Oblicz miary kątów trójkąta
. Oblicz miary kątów trójkąta 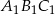 .
.
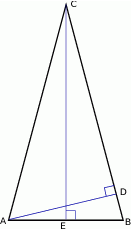
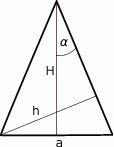
W trójkącie równoramiennym (patrz rysunek) długość podstawy wynosi  , zaś wysokości opuszczone odpowiednio na podstawę i ramię są równe
, zaś wysokości opuszczone odpowiednio na podstawę i ramię są równe 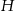 i
i  . Kąt między ramieniem trójkąta i wysokością opuszczoną na podstawę ma miarę
. Kąt między ramieniem trójkąta i wysokością opuszczoną na podstawę ma miarę  .
.
- Wyraź
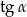 w zależności od wielkości
w zależności od wielkości  i
i 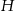 .
. - Wyraź
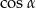 w zależności od wielkości
w zależności od wielkości  i
i 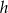 .
. - Wykaż, że jeśli
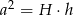 , to
, to 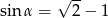 .
.
Oblicz miary kątów trójkąta, w którym długości boków tworzą ciąg geometryczny, a miary kątów tworzą ciąg arytmetyczny.

