Wiadomo, że 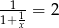 . Wówczas wartość wyrażenia
. Wówczas wartość wyrażenia 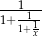 jest równa
jest równa
A)  B)
B) 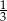 C)
C)  D)
D) 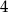 E)
E) 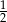
/Konkursy/Zadania testowe
Gwiazda, pokazana na rysunku obok, utworzona jest z 12 identycznych trójkątów równobocznych. Obwód gwiazdy jest równy 36 cm. Ile jest równy obwód zacieniowanego sześciokąta?
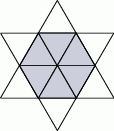
A) 6 cm B) 12 cm C) 18 cm D) 24 cm E) 30 cm
Na rysunku obok mamy trzy początkowe układanki. Ile jest potrzebnych białych kwadracików jednostkowych, aby ułożyć dziesiątą układankę w tym ciągu?
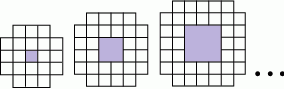
A) 76 B) 80 C) 84 D) 92 E) 100
Spośród trójkątów równoramiennych o ramionach długości 7 i podstawie, której długość wyraża się liczbą całkowitą, wybieramy trójkąt o największym obwodzie. Obwód ten jest równy
A) 14 B) 15 C) 21 D) 27 E) 28
Ile z poniższych działań ma wartość różną od 6?
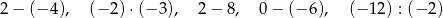
A) 0 B) 1 C) 2 D) 4 E) 5
Ile jest liczb dziesięciocyfrowych, które można napisać przy użyciu cyfr 1,2 i 3 tak, aby każde dwie sąsiednie cyfry w ich zapisach różniły się o jeden?
A) 16 B) 32 C) 64 D) 80 E) 100
Jakim procentem liczby elementów zboru 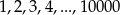 jest liczba tych jego elementów, które są kwadratami liczb naturalnych?
jest liczba tych jego elementów, które są kwadratami liczb naturalnych?
A) 1% B) 5% C) 10% D) 50% E) 0,1%
Różnica
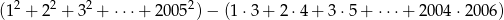
jest równa
A) 2000 B) 2004 C) 2005 D) 2006 E) 0
Ile jest liczb 2008–cyfrowych, których każde dwie kolejne cyfry tworzą liczbę podzielną przez 17 lub przez 23?
A) 5 B) 6 C) 7 D) 9 E) Więcej niż 9
Każda z liczb 257,338 ma tę własność, że jeśli jej cyfry zapiszemy w odwrotnej kolejności, to otrzymamy liczbę od niej większą. Ile jest wszystkich liczb trzycyfrowych o tej własności?
A) 124 B) 252 C) 280 D) 288 E) 360
W trójkącie równoramiennym  długość dwusiecznej
długość dwusiecznej  kąta przy wierzchołku
kąta przy wierzchołku 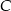 jest równa długości podstawy
jest równa długości podstawy 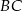 . Ile jest równa miara kąta
. Ile jest równa miara kąta 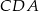 ?
?
A) 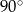 B)
B) 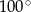 C)
C) 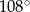 D)
D) 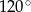 E) Nie da się tego rozstrzygnąć
E) Nie da się tego rozstrzygnąć
Kwadrat o polu 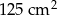 podzielono na pięć części o równych polach. Cztery z nich to kwadraty, a piąta to sześciokąt w kształcie litery L. Jaka jest długość najkrótszego boku tego sześciokąta?
podzielono na pięć części o równych polach. Cztery z nich to kwadraty, a piąta to sześciokąt w kształcie litery L. Jaka jest długość najkrótszego boku tego sześciokąta?

A) 1 cm B) 1,2 cm C) 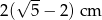 D)
D) 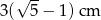 E)
E) 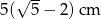
Dwa trójkąty równoboczne o obwodach po 18 cm nałożono na siebie tak, że odpowiednie pary ich boków są do siebie równoległe. Jaki jest obwód zacieniowanego sześciokąta?
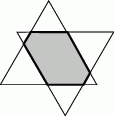
A) 9 cm B) 12 cm C) 13 cm D) 14 cm E) 18 cm
Rysunek obok przedstawia trójkąt równoramienny 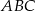 (
(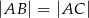 ), w którym
), w którym 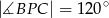 i
i 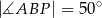 . Jaka jest miara kąta
. Jaka jest miara kąta 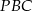 ?
?
A) 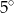 B)
B) 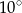 C)
C) 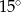 D)
D) 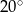 E)
E) 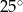
Z siatki składającej się z 8 trójkątów równobocznych można skleić ośmiościan foremny, jak na rysunku obok. Aby powstał ośmiościan magiczny, trzeba zamienić litery 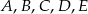 na liczby 2,4,6,7,8 (każdą literę na inną liczbę) w ten sposób, by sumy liczb na czterech ścianach przy każdym wierzchołku były sobie równe. Ile wówczas będzie równe
na liczby 2,4,6,7,8 (każdą literę na inną liczbę) w ten sposób, by sumy liczb na czterech ścianach przy każdym wierzchołku były sobie równe. Ile wówczas będzie równe 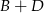 ?
?
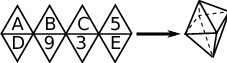
A) 6 B) 7 C) 8 D) 9 E) 10
Na rysunku poniżej punkty 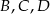 dzielą odcinek
dzielą odcinek 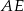 na cztery równe części. Narysowane trzy łuki są półokręgami o średnicach odpowiednio
na cztery równe części. Narysowane trzy łuki są półokręgami o średnicach odpowiednio 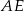 ,
, 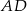 i
i 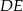 . Jaki jest stosunek długości półokręgu
. Jaki jest stosunek długości półokręgu 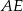 do sumy długości półokręgów
do sumy długości półokręgów 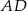 i
i  ?
?
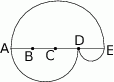
A) 1:2 B) 2:3 C) 2:1 D) 3:2 E) 1:1
Ile dróg prowadzi od górnego do dolnego końca przeciwprostokątnej dużego trójkąta, jeśli wolno poruszać się po bokach małych trójkątów w sposób przedstawiony na rysunku
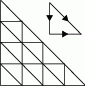
A) 16 B) 27 C) 64 D) 90 E) 111
Wszystkie potęgi liczby 3 oraz wszystkie te dodatnie liczby naturalne, które są skończonymi sumami różnych potęg liczby 3, ustawiamy w ciąg rosnący 1,3,4,9,10,12,13,…Ile jest równy setny wyraz tego ciągu?
A) 150 B) 981 C) 1234 D) 2401 E) 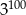
Starożytni Egipcjanie używali do wyznaczania kąta prostego linki z dwoma węzłami – złączone końce 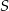 i
i 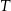 i owe węzły po naprężeniu linki tworzyły trójkąt prostokątny. Na takiej lince długości 12m węzeł
i owe węzły po naprężeniu linki tworzyły trójkąt prostokątny. Na takiej lince długości 12m węzeł 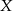 jest w odległości 3m od końca
jest w odległości 3m od końca 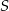 . W jakiej odległości od końca
. W jakiej odległości od końca 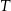 jest drugi węzeł, jeżeli po złączeniu końców otrzymujemy kąt prosty w węźle
jest drugi węzeł, jeżeli po złączeniu końców otrzymujemy kąt prosty w węźle 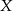 ?
?
![]()
A) 3m B) 4m C) 5m D) 6m E) Inna liczba
W roku 2008 cyfra jedności jest czterokrotnością cyfry tysięcy. Jaka jest minimalna liczba lat, które muszą upłynąć, by taka sytuacja się powtórzyła?
A) 10 B) 20 C) 100 D) 2008 E) Inna odpowiedź

