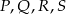W maratonie ulicznym udział wzięło 2009 zawodników. Liczba zawodników pokonanych przez Piotra, startującego w tym maratonie, okazała się trzy razy większa niż liczba zawodników, z którymi Piotr przegrał. Które miejsce zajął Piotr w tym maratonie?
A) 503 B) 501 C) 500 D) 1503 E) 1507
/Konkursy/Zadania testowe
Która z poniższych liczb jest największa?
A) 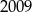 B)
B) 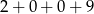 C)
C) 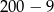 D)
D) 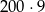 E)
E) 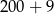
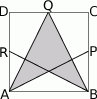
Z punktu 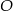 będącego środkiem kwadratu
będącego środkiem kwadratu 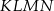 (patrz rysunek) prowadzimy odcinki
(patrz rysunek) prowadzimy odcinki 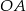 ,
, 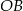 ,
, 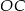 i
i 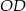 do boków tak, że
do boków tak, że 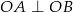 i
i 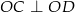 . Ile jest równe pole zacieniowanej części kwadratu, jeśli bok kwadratu ma długość 2?
. Ile jest równe pole zacieniowanej części kwadratu, jeśli bok kwadratu ma długość 2?
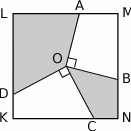
A) 1 B) 2 C) 2,5 D) 2,25 E) zależy od wyboru punktów B i C
W każdym z siedmiu kolejnych lat, zawsze 27 marca, urodził się jeden krasnoludek. Trzy najmłodsze krasnoludki mają razem 42 lata. Ile lat mają razem trzy najstarsze?
A) 51 B) 54 C) 57 D) 60 E) 63
Do narysowania przedstawionej na rysunku tablicy zawierającej 12 komórek użyto 5 prostych poziomych i 4 pionowych. Jeżeli użyjemy 6 prostych poziomych i 3 pionowych, to otrzymamy tablice o 10 komórkach. Jaką największą liczbę komórek można otrzymać, używając do narysowania tablicy 15 prostych?

A) 56 B) 27 C) 32 D) 40 E) 42
W diagramie obok każda litera oznacza cyfrę, przy czym różne litery oznaczają różne cyfry. Jaka cyfra, z poniżej podanych, kryje się pod literą 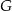 ?
?
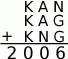
A) 1 B) 2 C) 3 D) 4 E) 5
Na różnych prostych równoległych  i
i 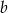 obrano 6 punktów: 4 punkty na prostej
obrano 6 punktów: 4 punkty na prostej  i 2 punkty na prostej
i 2 punkty na prostej 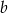 . Ile jest trójkątów, których wszystkie wierzchołki są w wybranych punktach?
. Ile jest trójkątów, których wszystkie wierzchołki są w wybranych punktach?
A) 6 B) 8 C) 12 D) 16 E) 18
Dwusieczna 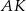 kąta
kąta 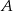 w trójkącie
w trójkącie 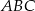 podzieliła ten trójkąt na dwa trójkąty o równych polach. Wówczas trójkąt
podzieliła ten trójkąt na dwa trójkąty o równych polach. Wówczas trójkąt 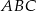 jest na pewno
jest na pewno
A) równoboczny B) równoramienny C) prostokątny D) ostrokątny E) rozwartokątny
Rozwiązaniem równania 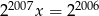 jest liczba
jest liczba
A) 1 B) 2 C) 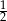 D)
D) 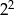 E)
E) 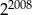
Jeżeli  jest liczbą całkowitą ujemną, to wśród poniższych liczb największą jest:
jest liczbą całkowitą ujemną, to wśród poniższych liczb największą jest:
A) 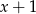 B)
B) 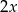 C)
C) 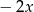 D)
D) 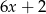 E)
E) 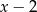
Jeżeli  i
i 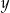 są liczbami całkowitymi o tej własności, że
są liczbami całkowitymi o tej własności, że 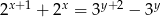 , to
, to  jest równe
jest równe
A) 0 B) 3 C) -1 D) 1 E) 2
Ile zer należy wpisać w miejsce  w zapisie dziesiętnym liczby
w zapisie dziesiętnym liczby 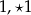 , aby liczba ta była mniejsza niż
, aby liczba ta była mniejsza niż 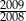 i jednocześnie większa niż
i jednocześnie większa niż 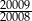 ?
?
A) 1 B) 2 C) 3 D) 4 E) 5
Na rysunku obok brzegi zaznaczonych kwadratów utworzone są przez części odcinka 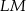 o długości 24 cm i przez odcinki łamanej
o długości 24 cm i przez odcinki łamanej 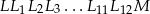 . Ile jest równa długość łamanej
. Ile jest równa długość łamanej 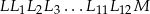 ?
?
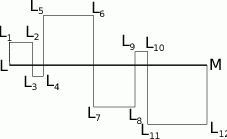
A) 106cm B) 96cm C) 72cm D) 56cm E) 48cm
Samochód ciężarowy, jadąc ze stałą prędkością, przebył drogę z miasta 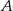 do miasta
do miasta 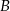 w czasie 1 godziny i 30 minut i drogę z miasta
w czasie 1 godziny i 30 minut i drogę z miasta 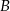 do miasta
do miasta 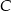 w czasie 1 godziny. Tę samą trasę pokonywał, również ze stałą prędkością, samochód osobowy, który z miasta
w czasie 1 godziny. Tę samą trasę pokonywał, również ze stałą prędkością, samochód osobowy, który z miasta 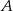 do miasta
do miasta 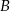 jechał 1 godzinę. Ile czasu jechał ten samochód z miasta
jechał 1 godzinę. Ile czasu jechał ten samochód z miasta 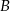 do miasta
do miasta 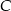 ?
?
A) 45 minut B) 40 minut C) 35 minut D) 30 minut E) 90 minut
Niech 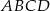 będzie kwadratem o boku 12 cm. Punkty
będzie kwadratem o boku 12 cm. Punkty 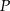 ,
, 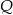 ,
, 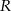 są odpowiednio środkami boków
są odpowiednio środkami boków 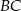 ,
, 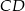 ,
, 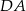 (rysunek obok). Pole zacieniowanego czworokąta jest równe
(rysunek obok). Pole zacieniowanego czworokąta jest równe
A) 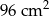 B)
B) 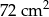 C)
C) 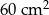 D)
D) 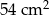 E)
E) 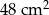
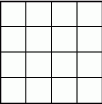
Na rysunku przedstawiono kwadratową tablicę 4x4 składającą się z 16 kwadracików jednostkowych. Ile jest równa największa możliwa liczba przekątnych, jakie można poprowadzić w tych kwadracikach jednostkowych w ten sposób, aby żadne dwie z nich nie przecinały się, ani nie miały wspólnych końców?
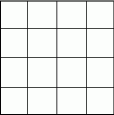
A) 8 B) 9 C) 10 D) 11 E) 12
Daniel ma 9 monet, każda o nominale 2 złotych, zaś jego siostra Ania ma 8 monet, każda o nominale 5 złotych. Jaką najmniejszą liczbę monet muszą oni między sobą wymienić, aby mieć równe kwoty?
A) 4 B) 5 C) 8 D) 12 E) Nie da się tego zrobić
Jaka jest najmniejsza liczba całkowita  , dla której liczba
, dla której liczba
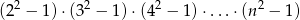
jest kwadratem liczby całkowitej?
A) 6 B) 8 C) 16 D) 27 E) Inna odpowiedź
W polach szachownicy 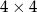 chcemy umieścić pionki w taki sposób, że liczby pionków w każdym wierszu i w każdej kolumnie szachownicy będą różne (w jednym polu można umieścić jeden lub więcej pionków, a także można pozostawić pole puste). Jaka jest minimalna liczba pionków, które można w taki sposób rozmieścić na szachownicy?
chcemy umieścić pionki w taki sposób, że liczby pionków w każdym wierszu i w każdej kolumnie szachownicy będą różne (w jednym polu można umieścić jeden lub więcej pionków, a także można pozostawić pole puste). Jaka jest minimalna liczba pionków, które można w taki sposób rozmieścić na szachownicy?
A) 7 B) 10 C) 14 D) 18 E) 28
W czworokącie 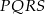 mamy
mamy 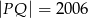 ,
, 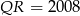 ,
, 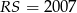 ,
, 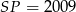 . Przy których wierzchołkach kąty wewnętrzne czworokąta mają zawsze miarę mniejszą niż
. Przy których wierzchołkach kąty wewnętrzne czworokąta mają zawsze miarę mniejszą niż 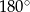 ?
?
A) 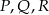 B)
B) 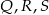 C)
C) 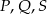 D)
D) 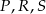 E)
E)