Przez dopisanie do siebie 20 słów KANGAROO powstał ciąg liter KANGAROOKANGAROO...KANGAROO. Na początek, w ciągu tym zmazujemy litery stojące na parzystych miejscach. Następnie, w tak otrzymanym nowym ciągu, zmazujemy litery stojące na parzystych miejscach. Postępowanie to kontynuujemy tak długo, aż pozostanie jedna litera. Jaka to litera?
A) K B) A C) N D) G E) O
/Konkursy/Zadania testowe
Duży kwadrat o polu 1 został podzielony na kwadraty, jak na rysunku obok. Pole małego zacieniowanego kwadratu jest równe.

A) 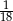 B)
B) 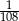 C)
C) 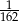 D)
D) 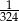 E)
E) 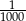
W prostokącie umieszczono sześć identycznych okręgów, jak na rysunku. Wierzchołki małego prostokąta są środkami czterech z tych okręgów. Wiadomo, że obwód małego prostokąta jest równy 60 cm. Ile jest równy obwód dużego prostokąta?
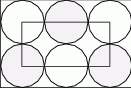
A) 90cm B) 140cm C)120 cm D)100 cm E)80 cm
Punkty 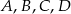 leżą na prostej w pewnym porządku. Wiadomo, że
leżą na prostej w pewnym porządku. Wiadomo, że 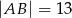 ,
, 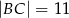 ,
, 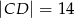 ,
, 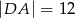 . Ile jest równa odległość pomiędzy skrajnie położonymi punktami?
. Ile jest równa odległość pomiędzy skrajnie położonymi punktami?
A) 25 B) 14 C) 38 D) 50 E) 39
Ile wynosi miara kąta ostrego w rombie, w którym długość boku jest równa średniej geometrycznej długości obu przekątnych?
A) 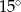 B)
B) 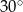 C)
C) 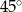 D)
D) 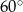 E)
E) 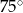
Liczba 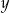 jest sumą cyfr liczby naturalnej
jest sumą cyfr liczby naturalnej  , a liczba
, a liczba  jest sumą cyfr liczby
jest sumą cyfr liczby 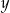 . Dla ilu liczb naturalnych
. Dla ilu liczb naturalnych  zachodzi równość
zachodzi równość 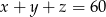 ?
?
A) 0 B) 1 C) 2 D) 3 E) Więcej niż 3
Spośród liczb wpisanych do tablicy obok wybieramy trzy liczby tak, aby żadne dwie z nich nie leżały w tym samym wierszu ani w tej samej kolumnie. Największa suma liczb w tak wybranych trójkach jest równa

A) 12 B) 15 C) 18 D) 21 E) 24
O godzinie 21:00 kierowca stwierdził, że jedzie z prędkością 100 km/h. Przy tej prędkości paliwa wystarczy mu na przejechanie 80 km. Najbliższa stacja paliw, gdzie może on zatankować, znajduje się w odległości 100 km. Kierowca wiedząc, że zużycie paliwa jest proporcjonalne do prędkości samochodu, postanowił w jak najkrótszym czasie dojechać do tej stacji. O której godzinie kierowca będzie na stacji?
A) 22:12 B) 22:15 C) 22:20 D) 22:25 E) 22:30
Turysta wybrał się na pieszą wędrówkę, składającą się najpierw z odcinka płaskiego, a następnie z krótkiej wspinaczki. Po dojściu do celu wrócił tą samą drogą, tzn. najpierw zszedł w dół, a potem ponownie przebył płaski odcinek. Cała wędrówka trwała 2 godziny. Ile kilometrów przewędrował jeśli wiadomo, że po płaskim terenie poruszał się z prędkością 4 km/h, wspinał się z prędkością 3 km/h, a schodził w dół z prędkością 6 km/h?
A) Za mało informacji, aby to obliczyć B) 6 km C) 7,5 km D) 8 km E) 10 km
Na poniższym rysunku w pierwszym wierszu umieszczono 11 kart i na każdej z nich 2 litery.

Drugi wiersz powstał z pierwszego przez zmianę kolejności niektórych kart, przy czym nie ujawniono dolnych liter. Który z poniższych układów liter może wystapić w dolnej linii drugiego wiersza?
A) ANJAMKILIOR
B) RLIIMKOJNAA
C) JANAMKILIRO
D) RAONJMILIKA
E) ANMAIKOLIRJ
W równości 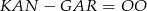 każda litera oznacza pewną cyfrę (różne litery odpowiadają różnym cyfrom). Jaka jest największa możliwa wartość liczby
każda litera oznacza pewną cyfrę (różne litery odpowiadają różnym cyfrom). Jaka jest największa możliwa wartość liczby 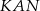 ?
?
A) 987 B) 876 C) 865 D) 864 E) 785
Ile liczb trzycyfrowych ma sumę cyfr równą 4?
A) 11 B) 6 C) 9 D) 8 E) 10
Dane są dwa zbiory liczb czterocyfrowych: zbiór 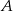 tych liczb, których iloczyn cyfr jest równy 25, oraz zbiór
tych liczb, których iloczyn cyfr jest równy 25, oraz zbiór 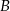 tych liczb, których iloczyn cyfr jest równy 15. Do którego zbioru należy więcej liczb i ile razy więcej liczb jest w tym zbiorze?
tych liczb, których iloczyn cyfr jest równy 15. Do którego zbioru należy więcej liczb i ile razy więcej liczb jest w tym zbiorze?
A) Zbiór 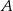 ma
ma  razy więcej elementów niż zbiór
razy więcej elementów niż zbiór 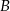 .
.
B) Zbiór 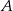 ma 2 razy więcej elementów niż zbiór
ma 2 razy więcej elementów niż zbiór 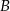 .
.
C) Zbiór 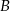 ma
ma 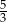 razy więcej elementów niż zbiór
razy więcej elementów niż zbiór 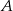 .
.
D) Zbiór 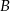 ma 2 razy więcej elementów niż zbiór
ma 2 razy więcej elementów niż zbiór 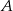 .
.
E) Oba zbiory mają po tyle samo elemantów
Pewien chłopiec w czwartki i piątki zawsze mówi prawdę, we wtorki zawsze kłamie, a w pozostałe dni tygodnia udziela odpowiedzi losowo, to znaczy czasem kłamie, a czasem mówi prawdę. Przez siedem kolejnych dni pytano go, jak ma na imię. Podczas pierwszych sześciu dni chłopiec udzielił następujących odpowiedzi, w takiej oto kolejności: Jan , Robert, Jan, Robert, Piotr, Robert. Jakiej odpowiedzi udzielił siódmego dnia?
A) Jan B) Robert C) Piotr D) Kasia E) Inna odpowiedź
Bieg maratoński rozgrywany jest na dystansie 42,196 km. Jarek wystartował do tego biegu o godzinie 13:37, a do mety dobiegł o godzinie 16:18. W ciągu ilu minut Jarek pokonał tę trasę?
A) 131 B) 91 C) 151 D) 185 E) 161
Na osi liczbowej zaznaczono liczby 2006 i 6002. Liczbą jednakowo odległą od nich jest
A) 3998 B) 4000 C) 4002 D) 4004 E) 4006
Kangurowa maszyna licząca może wykonać następujące operacje: pomnożyć daną liczbę przez 2 lub przez 3 albo podnieść daną liczbę do potęgi drugiej lub trzeciej. Którą z poniższych liczb możemy otrzymać, jeżeli maszyna rozpocznie działanie na liczbie 15 i wykona 5 operacji, kolejno na otrzymanych wcześniej wynikach?
A) 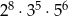 B)
B) 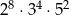 C)
C) 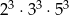 D)
D) 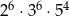 E)
E) 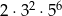
Liczbę pierwszą nazywamy specjalną jeżeli jest jednocyfrową liczbą pierwszą albo liczbą pierwszą o większej liczbie cyfr, ale taką, że po skreśleniu dowolnej skrajnej cyfry zawsze otrzymamy specjalną liczbę pierwszą. Ile jest specjalnych liczb pierwszych?
A) 4 B) 7 C) 8 D) 9 E) 11
Kwadrat o boku długości 10 „toczymy” bez poślizgu wzdłuż prostej (patrz rysunek) tak długo, aż punkt 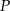 ponownie znajdzie się na tej prostej. Jaka jest długość drogi, którą zakreślił punkt
ponownie znajdzie się na tej prostej. Jaka jest długość drogi, którą zakreślił punkt 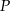 ?
?
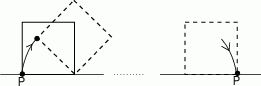
A) 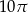 B)
B) 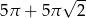 C)
C) 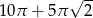 D)
D) 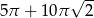 E)
E) 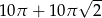
Ile razy od godziny 00:00 do godziny 23:59 zegarek elektroniczny pokaże wszystkie cyfry 2, 0, 0, 6 (w dowolnej kolejności)?
A) 2 B) 4 C) 5 D) 6 E) 12

