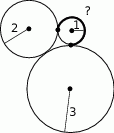
Basia buduje z zapałek kolejno układanki zgodnie ze schematem widocznym na rysunku obok, na którym zaznaczono układanki o numerach 1, 2, 3. O ile więcej zapałek zużyła do układanki o numerze 31 niż do układanki o numerze 30?
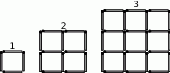
A) 124 B) 148 C) 61 D) 254 E) 120

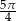
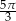
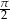
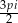
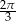
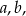 że
że 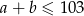 oraz
oraz 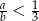 . Największy możliwy iloraz
. Największy możliwy iloraz 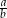 jest równy
jest równy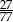
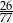
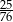
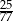
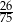
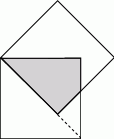
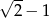
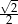
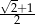
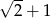
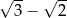
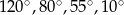 . Jaka jest miara najmniejszego kąta w trójkącie ostrokątnym?
. Jaka jest miara najmniejszego kąta w trójkącie ostrokątnym?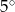
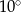
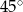
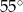
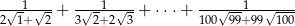 jest równa
jest równa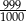
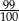
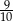
 stanowi 125% liczby
stanowi 125% liczby 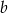 . Ile procent liczby
. Ile procent liczby  stanowi liczba
stanowi liczba 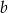 ?
?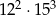 ?
?