Jacek w ramach przygotowań do konkursu „Kangur Matematyczny” postanowił rozwiązać po jednym zadaniu z kolejnych stron o numerach nieparzystych w swoim zbiorze zadań. Rozpoczął na stronie 15, a skończył na stronie na stronie 53. Ile zadań treningowych rozwiązał Jacek?
A) 19 B) 20 C) 27 D) 38 E) 53
/Konkursy/Zadania testowe
Liczbą dodatnią, której kwadrat jest większy od niej o 500% jest
A) 5 B) 6 C) 7 D) 8 E) 10
Jaka jest największa liczba cyfr, które należy usunąć z 1000-cyfrowej liczby 20082008…2008, aby suma pozostałych cyfr była równa 2008?
A) 260 B) 510 C) 520 D) 749 E) 746
Pierścienie boromejskie to takie trzy pierścienie, których nie można rozdzielić bez rozcinania, ale po usunięciu któregokolwiek z nich pozostałe dwa nie są ze sobą powiązane w żaden sposób. Który z rysunków przedstawia pierścienie boromejskie?

Trójkąty 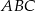 i
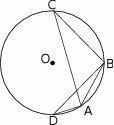
i 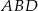 zostały wpisane w okrąg, jak na rysunku obok. Wiadomo, że
zostały wpisane w okrąg, jak na rysunku obok. Wiadomo, że 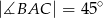 oraz
oraz 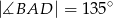 . Wówczas długości cięciw
. Wówczas długości cięciw 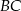 i
i 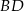 spełniają zależność
spełniają zależność
A) 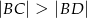
B) 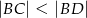
C) 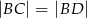
D) 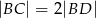
E) 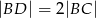
Na rysunku obok mały kwadrat wpisano w duży kwadrat. Pole małego kwadratu jest równe
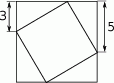
A) 16 B) 28 C) 34 D) 36 E) 49
W matematycznej pajęczynie na rysunku obok długości wszystkich odcinków wyrażają się liczbami całkowitymi. Ile jest równe  ?
?
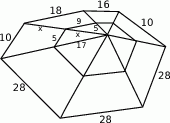
A) 11 B) 13 C) 15 D) 17 E) 19
Na rysunku obok dwa sześciokąty foremne mają wspólny bok. Jaka część pola równoległoboku jest zacieniowana?

A) 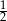 B)
B) 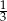 C)
C) 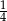 D)
D) 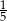 E)
E) 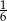
Na powierzchni piłki namalowano trzy jednakowe okręgi, dzielące ją na osiem jednakowych części, jak na rysunku obok. Trzmiel, który usiadł na piłce w punkcie przecięcia okręgów, wędruje po namalowanych okręgach w taki sposób, że po przejściu ćwiartki okręgu w punkcie przecięcia z innym okręgiem zawsze skręca na przemian w w prawo albo w lewo, tj. w prawo, gdy w poprzedzającym punkcie skręcał w lewo, natomiast w lewo, gdy w poprzedzającym punkcie skręcał w prawo. Jaka jest najmniejsza liczba ćwiartek okręgów, które musi przejść trzmiel aby ponownie znalazł się w punkcie, z którego wyruszył?
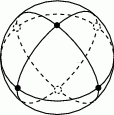
A) 6 B) 9 C) 12 D) 15 E) 18
W pokoju bawią się koty i psy. Liczba kocich łap jest dwa razy większa niż liczba psich nosów. Liczba kotów jest
A) dwa razy większa od liczby psów.
B) równa liczbie psów.
C) równa połowie liczby psów.
D) 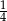 liczby psów.
liczby psów.
E) 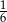 liczby psów.
liczby psów.
Pole trójkąta przedstawionego na rysunku jest równe 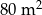 , a promień każdego okręgu w środku w jego wierzchołku jest równy 2 m. Ile metrów kwadratowych ma pole zacieniowanej figury?
, a promień każdego okręgu w środku w jego wierzchołku jest równy 2 m. Ile metrów kwadratowych ma pole zacieniowanej figury?
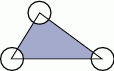
A) 76 B) 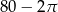 C)
C) 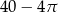 D)
D) 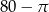 E)
E) 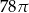
Z jabłek, śliwek, pomarańczy i bananów układamy na półce kompozycje, kładąc kolejno owoc za owocem. Kompozycja jest kompletna, gdy bezpośrednio za owocem dowolnego rodzaju przynajmniej raz leży owoc każdego innego rodzaju. Z ilu owoców składa się najmniej liczna kompletna kompozycja owoców?
A) 13 B) 8 C) 16 D) 4 E) 12
Na rysunku obok, trójkąt i kwadrat mają równe obwody. Ile wynosi obwód całej figury (pięciokąta)?
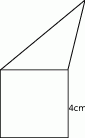
A) 12 cm B) 24 cm C) 28 cm D) 32 cm E) 20 cm
Na kartce napisano w jednej linii kilka różnych liczb całkowitych dodatnich nie większych niż 10. Oglądając tę kartkę, Mirek stwierdził ze zdumieniem, że w każdej parze sąsiednich liczb jedna z nich dzieli drugą. Ile co najwyżej liczb mogło byc napisanych na tej kartce?
A) 6 B) 7 C) 8 D) 9 E) 10
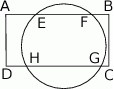
Okrąg przecina boki prostokąta 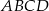 w punktach
w punktach 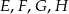 , jak na rysunku obok. Wiadomo, że
, jak na rysunku obok. Wiadomo, że 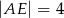 ,
, 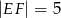 ,
, 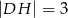 . Ile wynosi długość odcinka
. Ile wynosi długość odcinka 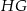 ?
?
A) 6 B) 7 C) 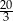 D) 8 E) 9
D) 8 E) 9
Klasa liczy 9 chłopców i 13 dziewcząt. Połowa uczniów tej klasy jest przeziębiona. Co najmniej ile dziewcząt jest przeziębionych?
A) 0 B) 1 C) 2 D) 3 E) 4
Parę liczb całkowitych nazywamy dobrą, jeśli ich suma jest równa ich iloczynowi. Ile jest dobrych par liczb?
A) 1 B) 2 C) 3 D) 5 E) Nieskończenie wiele
Która z poniższych liczb jest wielokrotnością liczby 3?
A) 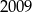 B)
B) 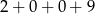 C)
C) 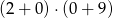 D)
D) 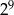 E)
E) 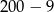
Który z poniższych wykresów jest wykresem funkcji 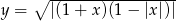 ?
?

W kwadraciki tablicy 3x3 wpisane są liczby naturalne (rysunek obok). Ada wykreśliła z tablicy 4 liczby, a następnie Maria wykreśliła z pozostałych także 4 liczby. Okazało się, że suma liczb skreślonych przez Adę jest trzy razy większa od sumy liczb skreślonych przez Marię. Jaka liczba pozostała nie skreślona ?

A) 4 B) 7 C) 14 D) 23 E) 24

