Aby otrzymać liczbę 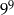 , należy liczbę
, należy liczbę 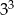 podnieść do potęgi
podnieść do potęgi
A) 2 B) 3 C) 6 D) 9 E) 18
/Konkursy/Zadania testowe
Dany jest kwadrat 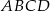 . Odcinki poprowadzone z punktów
. Odcinki poprowadzone z punktów 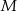 i
i 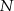 do jego wierzchołków dzielą go na osiem części. Na rysunku zaznaczono pola trzech z nich. Jakie jest pole zacieniowanej części?
do jego wierzchołków dzielą go na osiem części. Na rysunku zaznaczono pola trzech z nich. Jakie jest pole zacieniowanej części?
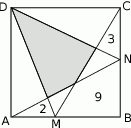
A) 14 B) 18 C) 11 D) 12 E) 9
Michał na egzaminie testowym odpowiedział poprawnie na 80% pytań, a na pozostałe 5 pytań nie udzielił odpowiedzi. Ile było pytań w teście?
A) 20 B) 25 C) 30 D) 35 E) 40
Pięcioosobowe zespoły z dwóch szkół mają rozegrać pomiędzy sobą zawody w tenisie stołowym par. Każda para zawodników jednej szkoły musi rozegrać z każdą parą zawodników z drugiej szkoły dokładnie jedno spotkanie. W ilu spotkaniach zagra każdy z 10 zawodników?
A) 10 B) 20 C) 30 D) 40 E) 50
Uczeń ma 2009 sześciennych klocków o krawędzi długości 1 oraz 2009 kolorowych kwadratowych naklejek o boku długości 1. Uczeń ten skleił ze wszystkich klocków prostopadłościan i okleił całą jego powierzchnię naklejkami, przyklejając dokładnie po jednej do każdej ściany klocka, tworzącej tę powierzchnię. Okazało się, że uczniowi pozostały jeszcze naklejki. Ile ich pozostało?
A) Więcej niż 1000 B) 763 C) 476 D) 49 E) Opisana sytuacja jest niemożliwa
W równości 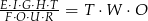 różnym literom odpowiadają różne cyfry, a jednakowym literom jednakowe cyfry. Ile wartości może przyjmować iloczyn
różnym literom odpowiadają różne cyfry, a jednakowym literom jednakowe cyfry. Ile wartości może przyjmować iloczyn 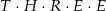 ?
?
A) 1 B) 2 C) 3 D) 4 E) 5
Ile jest liczb całkowitych dodatnich, których kwadrat i sześcian mają tę samą liczbę cyfr w zapisach w systemie dziesiątkowym?
A) 0 B) 3 C) 4 D) 9 E) Nieskończenie wiele.
75% połowy  liczby 240 jest równe
liczby 240 jest równe
A) 120 B) 90 C) 80 D) 60 E) 40
W każde pole tablicy o wymiarach 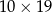 wpisujemy 0 lub 1. Wyznaczamy sumy liczb stojących w każdym wierszu i w każdej kolumnie. Największa możliwa liczba różnych sum, które można w ten sposób otrzymać, jest równa
wpisujemy 0 lub 1. Wyznaczamy sumy liczb stojących w każdym wierszu i w każdej kolumnie. Największa możliwa liczba różnych sum, które można w ten sposób otrzymać, jest równa
A) 9 B) 10 C) 15 D) 19 E) 29
Bryła widoczna na rysunku obok jest zbudowana z dwóch sześcianów o krawędziach długości 1 cm i 3 cm. Jakie jest pole powierzchni tej bryły?
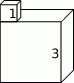
A) 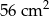 B)
B) 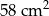 C)
C) 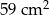 D)
D) 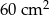 E)
E) 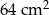
Wyspę zamieszkują kłamcy i prawdomówni (kłamcy zawsze kłamią, a prawdomówni zawsze mówią prawdę). Pewnego dnia zebrało się 12 wyspiarzy, wśród których byli kłamcy i prawdomówni i wygłosiło kilka stwierdzeń. Dwóch z nich powiedziało: „Dokładnie dwie osoby wśród nas dwunastu to kłamcy”. Każda z następnych czterech osób powiedziała: „Dokładnie cztery osoby wśród nas dwunastu to kłamcy”. Natomiast każda z pozostałych sześciu osób stwierdziła: „Dokładnie sześć osób wśród nas dwunastu to kłamcy". Ilu jest kłamców wśród tej dwunastki wyspiarzy?
A) 2 B) 4 C) 6 D) 8 E) 10
Planujemy pokolorować kratki kwadratu, używając kolorów 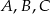 i
i 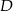 w taki sposób, by żadne dwie kratki o wspólnym boku lub wierzchołku nie były pokolorowane tym samym kolorem. Pewne kratki są już pokolorowane (patrz rysunek).
w taki sposób, by żadne dwie kratki o wspólnym boku lub wierzchołku nie były pokolorowane tym samym kolorem. Pewne kratki są już pokolorowane (patrz rysunek).

Jakie są możliwe pokolorowania kratki zacieniowanej?
A) Tylko 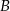 . B) Tylko
. B) Tylko 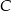 . C) Tylko
. C) Tylko 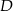 . D) Albo
. D) Albo 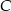 , albo
, albo 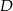 .
.
E) Kwadratu tego nie można tak pokolorować.
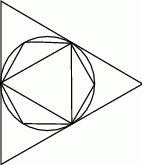
Trójkąt równoboczny i sześciokąt foremny wpisano w okrąg, na którym opisano trójkąt równoboczny (patrz rysunek). Niech 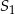 oznacza pole dużego trójkąta,
oznacza pole dużego trójkąta, 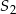 pole małego trójkąta, a
pole małego trójkąta, a 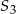 pole sześciokąta foremnego. Która z równości jest prawdziwa?
pole sześciokąta foremnego. Która z równości jest prawdziwa?
A) 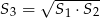 B)
B) 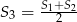 C)
C) 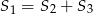 D)
D) 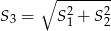 E)
E) 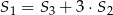
Wyspę zamieszkują prawdomówni i kłamcy. Prawdomówni zawsze mówią prawdę, a kłamcy zawsze kłamią. 25 mieszkańców tej wyspy ustawiło się w kolejkę. Każda osoba z kolejki, z wyjątkiem pierwszej, powiedziała: Osoba stojąca bezpośrednio przede mną to kłamca, natomiast osoba stojąca jako pierwsza w kolejce powiedziała: Wszyscy stojący za mną to kłamcy. Ilu kłamców stało w tej kolejce?
A) 24 B) 13 C) 12 D) 0 E) Nie można obliczyć
W kwadracie o boku długości 1 narysowano dwa okręgi jak na rysunku. Jaką wartość ma suma długości promieni tych okręgów?

A) 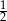
B) 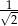
C) 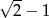
D) 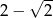
E) Suma ta zależy od stosunku promieni tych okręgów
Która z liczb jest największa?
A) 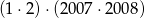
B) 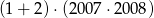
C) 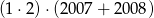
D) 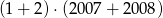
E) 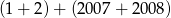
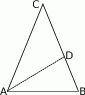
W trójkącie równoramiennym 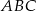 , w którym
, w którym 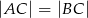 , poprowadzono dwusieczną
, poprowadzono dwusieczną 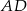 kąta przy wierzchołku
kąta przy wierzchołku 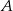 (patrz rysunek), przy czym
(patrz rysunek), przy czym 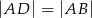 . Jaka jest miara kąta
. Jaka jest miara kąta 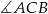 ?
?
A) 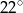 B)
B) 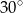 C)
C) 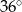 D)
D) 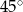 E)
E) 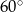
Na płaszczyźnie zaznaczono punkty 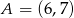 ,
, 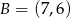 ,
, 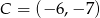 ,
, 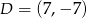 i
i 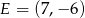 . Który z poniższych odcinków jest równoległy do osi
. Który z poniższych odcinków jest równoległy do osi 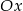 ?
?
A) 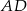 B)
B) 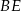 C)
C) 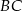 D)
D) 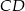 E)
E) 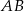
Andrzej, Mietek i Zbyszek rzucają kolejno kostką do gry. Andrzej wygrywa, jeżeli wyrzuci 1,2 lub 3. Mietek wygrywa, jeżeli wyrzuci 4 lub 5. Zbyszek wygrywa, jeżeli wyrzuci 6. Najpierw kostką rzuca Andrzej, potem Mietek, potem Zbyszek, potem znowu Andrzej, znowu Mietek, itd. Gra się kończy, gdy któryś z nich wygra. Jakie jest prawdopodobieństwo, że wygra Zbyszek?
A)  B)
B)  C)
C) 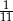 D)
D) 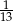 E) 0
E) 0
W wyniku ankiety przeprowadzonej z udziałem 2006 uczestników stwierdzono, że 1500 spośród nich uczestniczyło w konkursie „Kangur Matematyczny”, a 1200 w konkursie języka angielskiego. Ilu uczestników ankiety brało udział w obydwu konkursach, jeżeli wiadomo, że 6 ankietowanych nie wzięło udziału w żadnym z konkursów?
A) 300 B) 500 C) 600 D) 700 E) 1000

