W pokoju znajdowała się pewna liczba osób. Ich średni wiek równy był liczbie osób znajdujących się w pokoju. Gdy do pokoju wszedł 29 letni człowiek, okazało się, że średni wiek był równy liczbie osób w pokoju. Ile osób znajdowało się na początku w pokoju?
A) 14 B) 15 C) 16 D) 17 E) 18
/Konkursy/Zadania testowe
Rakietą podróżowała grupa kosmitów. Każdy z nich ubrany był w kombinezon w jednym z trzech kolorów: zielonym, pomarańczowym, niebieskim. Każdy ubrany na zielono kosmita miał dwa czułki, każdy ubrany na pomarańczowo miał trzy czułki, a każdy ubrany na niebiesko miał pięć czułków. Wszystkich kosmitów ubranych na zielono było tylu, ilu ubranych na pomarańczowo, a ubranych na niebiesko było o 10 więcej niż ubranych na zielono. Wszyscy razem mieli 250 czułków. Ilu ubranych na niebiesko kosmitów podróżowało rakietą?
A) 15 B) 20 C) 25 D) 30 E) 40
Prostokąt, który widzimy obok na rysunku, podzielono na 7 kwadratów. Bok każdego z zacieniowanych kwadratów ma długość 8. Jaką długość ma bok dużego białego kwadratu?

A) 16 B) 18 C) 20 D) 24 E) 30
Jacek powiedział, że 25% jego książek to opowiadania, a 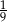 to poezje. Wiadomo, że ma on co najmniej 50 książek, ale nie więcej niż 100. Ile książek ma Jacek?
to poezje. Wiadomo, że ma on co najmniej 50 książek, ale nie więcej niż 100. Ile książek ma Jacek?
A) 50 B) 56 C) 64 D) 72 E) 93
Ile jest liczb naturalnych, o sumie cyfr równej 10, w których zapisie mogą występować tylko cyfry 1 lub 3?
A) 28 B) 34 C) 35 D) 55 E) 56
Dodatnia liczba naturalna  jest najmniejszą liczbą taką, że
jest najmniejszą liczbą taką, że 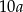 jest kwadratem pewnej liczby naturalnej, a
jest kwadratem pewnej liczby naturalnej, a 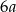 sześcianem pewnej liczby naturalnej. Ile różnych dzielników ma liczba
sześcianem pewnej liczby naturalnej. Ile różnych dzielników ma liczba  ?
?
A) 30 B) 40 C) 54 D) 72 E) 96
Czworo przyjaciół zamierza na przyjęciu dać sobie nawzajem prezenty w taki sposób, że każdy da tylko jednej osobie prezent, i każdy otrzyma prezent tylko od jednej osoby (oczywiście nikt nie daje prezentu sobie). Na ile sposobów można to zrobić?
A) 9 B) 10 C) 12 D) 16 E) 24
Ile czterocyfrowych liczb, których wszystkie cztery cyfry są różne, dzieli się przez 2006?
A) 1 B) 2 C) 3 D) 4 E) 5
Dwa wzajemnie styczne okręgi o równych promieniach mają środki w dwóch przeciwległych wierzchołkach kwadratu. Kolejne dwa okręgi, o środkach w pozostałych wierzchołkach kwadratu, są styczne zewnętrznie do każdego z dwóch poprzednich okręgów (patrz rysunek). Ile razy promień większego okręgu jest większy od promienia mniejszego okręgu?
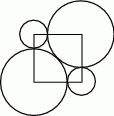
A) 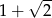 B)
B) 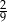 C)
C) 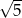 D)
D) 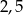 E)
E) 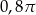
Kangur wymyślił nowe działanie  w zbiorze liczb naturalnych dodatnich. Podał kilka przykładów:
w zbiorze liczb naturalnych dodatnich. Podał kilka przykładów: 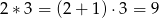 ;
; 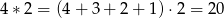 ;
; 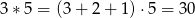 . Jaki jest wynik działania
. Jaki jest wynik działania 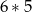 ?
?
A) 30 B) 90 C) 105 D) 210 E) 315
Jeżeli 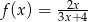 oraz
oraz 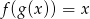 , to
, to
A) 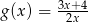 B)
B) 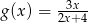 C)
C) 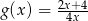 D)
D) 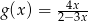 E)
E) 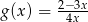
W grze losowej wygrywają kupony o numerach co najmniej 5-cyfrowych, w których co najwyżej 3 cyfry są większe od 2. Ile jest kuponów wygrywających wśród kuponów o numerach 1022, 22222, 102334, 213343, 3042531?
A) 1 B) 2 C) 3 D) 4 E) 5
Dana jest kula o promieniu 3 i o środku w początku układu współrzędnych. Ile punktów na powierzchni tej kuli ma wszystkie współrzędne całkowite?
A) 30 B) 24 C) 12 D) 6 E) 3
Czarek myśli, że każdy trójkąt równoramienny jest ostrokątny. Który z poniższych przykładów pokazuje, że Czarek nie ma racji?

W trójkącie 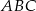 miara kąta wewnętrznego przy wierzchołku
miara kąta wewnętrznego przy wierzchołku 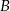 jest równa
jest równa 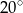 , a miara kąta wewnętrznego przy wierzchołku
, a miara kąta wewnętrznego przy wierzchołku 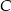 jest równa
jest równa 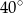 . Ponadto długość dwusiecznej kąta przy wierzchołku
. Ponadto długość dwusiecznej kąta przy wierzchołku 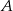 jest równa 2. Ile wynosi różnica
jest równa 2. Ile wynosi różnica 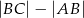 ?
?
A) 1 B) 1,5 C) 2 D) 4 E) Nie można jej jednoznacznie wyznaczyć.
Punkt 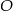 jest środkiem pięciokąta foremnego. Jaką częścią pięciokąta jest zacieniowany obszar?
jest środkiem pięciokąta foremnego. Jaką częścią pięciokąta jest zacieniowany obszar?
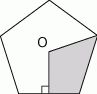
A) 10% B) 20% C) 25% D) 30% E) 40%
3–piramida to stos utworzony z trzech warstw kul przedstawionych na rysunku. W ten sam sposób otrzymujemy 4–piramidę, 5-piramidę, itd.
Gdy usuniemy wszystkie kule „ścian bocznych” i „podstawy” 8-piramidy, to otrzymamy
![]()
A) 3–piramidę B) 4–piramidę C) 5–piramidę D) 6–piramidę E) 7–piramidę
Na okręgu rozmieszczono liczby: 1,2,3. Pomiędzy każde dwie sąsiednie liczby wpisano ich sumy, otrzymując na okręgu sześć liczb 1,3,2,5,3,4. Operację wpisywania sum liczb sąsiednich powtórzono jeszcze trzy razy. W rezultacie otrzymano na okręgu 48 liczb. Ile wynosi ich suma?
A) 162 B) 1458 C) 486 D) 144 E) 210
Magda napisała ciąg liczb, w którym każda liczba, począwszy od trzeciej, była sumą dwóch liczb ją poprzedzających. Czwartą liczbą w tym ciągu była liczba 6, a szóstą 15. Ile była równa siódma liczba w tym ciągu?
A) 9 B) 16 C) 21 D) 22 E) 24
Tomek urodził się w dniu 20 urodzin swojej matki, i potem oboje obchodzili równocześnie swoje urodziny. Ile razy wiek Tomka, liczony w dniu jego urodzin, będzie dzielnikiem wieku jego matki?
A) 4 B) 5 C) 6 D) 7 E) 8

