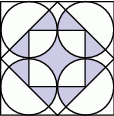
Rysunek obok przedstawia kwadratową płytkę. Narysowane na niej linie krzywe są ćwiartkami okręgów o promieniu równym połowie boku płytki. Długość takiej ćwiartki jest równa 5 dm. Z szesnastu takich płytek budujemy kwadrat. Jaką maksymalną długość może mieć nieprzerwana linia utworzona z ćwiartek tych okręgów?

A) 75 dm B) 100 dm C) 105 dm D) 110 dm E) 80 dm

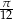
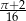
 i
i 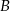 trójkąta
trójkąta 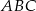 połączymy odcinkami z dwoma różnymi punktami leżącymi na przeciwległym boku, to odcinki te podzielą ten trójkąt na dziewięć części (patrz rysunek). Na ile części zostanie podzielony trójkąt, jeżeli każdy z wierzchołków
połączymy odcinkami z dwoma różnymi punktami leżącymi na przeciwległym boku, to odcinki te podzielą ten trójkąt na dziewięć części (patrz rysunek). Na ile części zostanie podzielony trójkąt, jeżeli każdy z wierzchołków 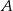 i
i 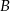 połączymy odcinkami z czterema punktami (różnymi od wierzchołków) leżącymi na przeciwległym do nich boku?
połączymy odcinkami z czterema punktami (różnymi od wierzchołków) leżącymi na przeciwległym do nich boku? 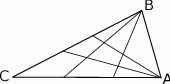

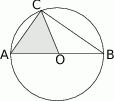
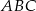 opisano okrąg o środku
opisano okrąg o środku 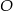 (rysunek obok). Zacieniowany trójkąt ma pole równe
(rysunek obok). Zacieniowany trójkąt ma pole równe 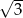 . Ile jest równe pole trójkąta
. Ile jest równe pole trójkąta 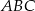 ?
? 
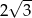
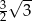
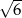
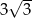
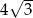
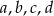 i
i  są takie, że
są takie, że 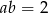 ,
, 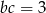 ,
, 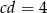 ,
, 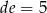 . Jaką wartość ma
. Jaką wartość ma 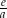 ?
?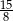


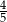
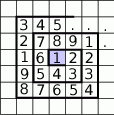
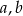 ze zbioru
ze zbioru 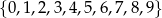 spełnia równanie
spełnia równanie 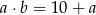 ?
?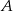 jest prawdziwa, to odpowiedź
jest prawdziwa, to odpowiedź 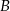 także jest prawdziwa.
także jest prawdziwa. 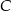 nie jest prawdziwa, to odpowiedź
nie jest prawdziwa, to odpowiedź 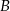 także nie jest prawdziwa.
także nie jest prawdziwa. 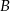 nie jest prawdziwa, to ani odpowiedź
nie jest prawdziwa, to ani odpowiedź 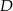 , ani
, ani 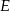 nie jest prawdziwa.
nie jest prawdziwa.