Organizacja międzynarodowa liczy 32 członków. Ilu członków będzie liczyła ta organizacja po 3 latach, jeśli rokrocznie ich liczba wzrasta o 50%?
A) 182 B) 128 C) 108 D) 96 E) 80
/Konkursy/Zadania testowe
Na osi liczbowej zaznaczono ułamki 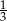 i
i 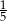 .
.
![]()
Która z liter oznacza ułamek 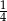 ?
?
A)  B)
B) 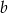 C)
C)  D)
D) 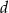 E)
E) 
Na rysunku przedstawiony jest fragment wykresu funkcji 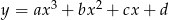 . Ile wynosi
. Ile wynosi 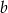 ?
?
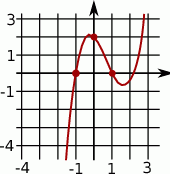
A) -4 B) -2 C) 0 D) 2 E) 4
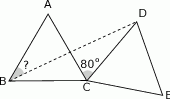
Na rysunku obok trójkąty 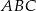 i
i 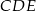 są równoboczne i przystające. Jaka jest miara kąta
są równoboczne i przystające. Jaka jest miara kąta 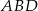 jeżeli miara kąta
jeżeli miara kąta 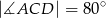 ?
?
A) 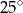 B)
B) 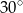 C)
C) 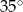 D)
D) 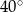 E)
E) 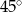
Butelka o pojemności 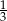 litra jest w
litra jest w  swojej pojemności wypełniona sokiem. Ile soku pozostanie w butelce po odlaniu
swojej pojemności wypełniona sokiem. Ile soku pozostanie w butelce po odlaniu 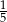 litra?
litra?
A) 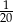 litra B)
litra B) 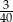 litra C) 0,13 litra D)
litra C) 0,13 litra D)  litra E) Butelka będzie pusta
litra E) Butelka będzie pusta
Jaka jest najmniejsza liczba 10-cyfrowa, którą można utworzyć przez dopisanie do siebie w dowolnej kolejności sześciu liczb: 309, 41, 5, 7, 68 i 2?
A) 1 234 567 890
B) 1 023 456 789
C) 3 097 568 241
D) 2 309 415 687
E) 2 309 416 857
Na płaszczyźnie dany jest kwadrat 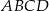 o boku długości 1. Rozważamy wszystkie kwadraty, które mają przynajmniej dwa wierzchołki wspólne z kwadratem
o boku długości 1. Rozważamy wszystkie kwadraty, które mają przynajmniej dwa wierzchołki wspólne z kwadratem 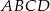 . Jakie jest pole obszaru pokrytego przez te kwadraty?
. Jakie jest pole obszaru pokrytego przez te kwadraty?
A) 5 B) 6 C) 7 D) 8 E) 9
Iloma zerami kończy się dziesiętny zapis iloczynu dziesięciu początkowych liczb pierwszych?
A) 0 B) 1 C) 2 D) 3 E) 4
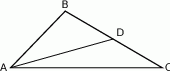
W trójkącie 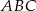 poprowadzono środkową
poprowadzono środkową 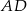 . Kąt
. Kąt 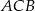 ma miarę
ma miarę 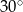 , a kąt
, a kąt 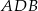 ma miarę
ma miarę 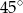 . Jaka jest miara kąta
. Jaka jest miara kąta 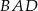 ?
?
A) 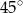 B)
B) 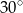 C)
C) 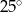 D)
D) 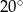 E)
E) 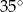
Dla ilu wartości rzeczywistych parametru  równanie
równanie 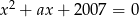 ma dwa rozwiązania całkowitoliczbowe?
ma dwa rozwiązania całkowitoliczbowe?
A) 3 B) 4 C) 6 D) 8 E) 2007
Dodatnia liczba naturalna  ma dwa dzielniki naturalne, podczas gdy liczba
ma dwa dzielniki naturalne, podczas gdy liczba 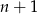 ma trzy dzielniki naturalne. Ile dzielników naturalnych ma liczba
ma trzy dzielniki naturalne. Ile dzielników naturalnych ma liczba 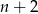 ?
?
A) 2 B) 3 C) 4 D) 5 E) Zależy to od 
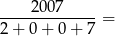
A) 1003 B) 75 C) 223 D) 213 E) 123
Mechaniczny kangurek porusza się po polach planszy przedstawionej obok na rysunku, startując z pola A3 w kierunku wskazanym strzałką. Kangurek porusza się tylko do przodu, przeskakując w pojedynczym skoku ze środka kratki, w której się znajduje, w środek kratki sąsiedniej (kratki są sąsiednie, gdy mają wspólny bok). Kangurek nie może wyskoczyć poza planszę, ani nie może wskoczyć na pola zacieniowane. Jeśli nie może wykonać skoku do przodu, to wykonuje obrót o 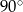 w prawo i porusza się dalej. Jeżeli po obrocie nie może wykonać skoku, to kończy wędrówkę. Na jakim polu zatrzyma się kangurek?
w prawo i porusza się dalej. Jeżeli po obrocie nie może wykonać skoku, to kończy wędrówkę. Na jakim polu zatrzyma się kangurek?

A) B2 B) A1 C) E1 D) D1 E) nigdy się nie zatrzyma
Dla pewnej liczby naturalnej  zachodzi równość
zachodzi równość
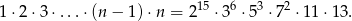
Ile wynosi  ?
?
A) 13 B) 14 C) 15 D) 16 E) 17
Jedna ze ścian sześcianu została rozcięta wzdłuż przekątnych, jak na rysunku obok. Dwa z podanych poniżej rysunków nie przedstawiają siatki tego sześcianu. Które?

A) 1 i 3 B) 1 i 5 C) 3 i 4 D) 3 i 5 E) 2 i 4
Na rysunku obok przedstawiony jest kwadrat  o boku długości 1 oraz łuki okręgów o środkach
o boku długości 1 oraz łuki okręgów o środkach 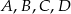 .
.
Ile wynosi długość odcinka 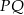 ?
?
A) 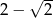 B)
B)  C)
C) 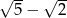 D)
D) 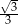 E)
E) 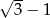
Ile nieujemnych liczb całkowitych mniejszych od 100 można otrzymać jako sumę dziewięciu kolejnych liczb całkowitych?
A) 13 B) 12 C) 11 D) 10 E) 9
Brytyjski matematyk August de Morgan twierdził, że miał  lat w roku
lat w roku 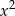 . Wiadomo, że de Morgan umarł w roku 1899. W którym roku się urodził?
. Wiadomo, że de Morgan umarł w roku 1899. W którym roku się urodził?
A) 1806 B) 1848 C) 1849 D) 1899 E) Inna odpowiedź
W sześcianie odcięto wszystkie naroża w sposób pokazany na rysunku obok. Ile ścian ma otrzymany w ten sposób wielościan?
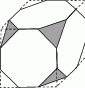
A) 10 B) 18 C) 12 D) 16 E) 14
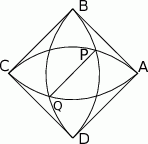
W trójkącie 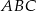 punkt
punkt 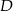 jest środkiem boku
jest środkiem boku 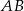 , punkt
, punkt 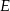 środkiem odcinka
środkiem odcinka 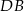 , a
, a 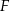 środkiem boku
środkiem boku 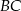 . Jeśli pole trójkąta
. Jeśli pole trójkąta 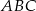 jest równe 96, to pole trójkąta
jest równe 96, to pole trójkąta 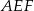 jest równe
jest równe
A) 16 B) 24 C) 32 D) 36 E) 48

