Franek i Andrzej ukończyli bieg na 200 metrów. Andrzej przebiegł ten dystans w pół minuty, a Franek w setną część godziny. Kto był szybszy i o ile sekund?
A) Andrzej, o 36 sekund
B) Franek, o 24 sekund
C) Andrzej, o 6 sekund
D) Franek, o 6 sekund
E) Obaj mieli równy czas
/Konkursy/Zadania testowe
Wartość wyrażenia 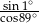 jest równa
jest równa
A) 0 B) 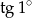 C)
C) 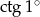 D)
D) 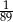 E)
E) 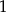
Mama przygotowała na zimę sok wiśniowy, którym można napełnić dokładnie 12 dużych słoików albo dokładnie 20 mniejszych słoików. Mama napełniła już 9 dużych słoików i resztę postanowiła rozlać do mniejszych słoików. Ile takich słoików napełni pozostałym sokiem?
A) 3 B) 4 C) 5 D) 6 E) 8
Niech 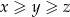 będą dodatnimi liczbami rzeczywistymi takimi, że
będą dodatnimi liczbami rzeczywistymi takimi, że 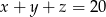 . Które z poniższych zdań jest prawdziwe?
. Które z poniższych zdań jest prawdziwe?
A) Zawsze 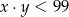
B) Zawsze 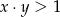
C) Zawsze 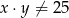
D) Zawsze 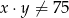
E) Żadne z poprzednich zdań nie jest prawdziwe.
Zepsuty kalkulator nie wyświetla cyfry 1. Na przykład, jeśli wpiszemy liczbę 3131, to pokazuje on liczbę 33 bez żadnych odstępów między cyframi. Michał napisał na tym kalkulatorze pewną liczbę sześciocyfrową i na wyświetlaczu kalkulatora pojawiła się liczba 2007. Dla ilu liczb mogło się tak zdarzyć?
A) 12 B) 13 C) 14 D) 15 E) 16
Pewna wyspa zamieszkana jest wyłącznie przez kłamców i przez rycerzy. Każdy kłamca zawsze kłamie, każdy rycerz zawsze mówi prawdę. Wyspiarz Abacki, zapytany, kim jest on i kim jest jego sąsiad Babacki, odpowiedział: „Przynajmniej jeden z nas jest kłamcą”. Które z poniższych zdań jest prawdziwe?
A) Żaden mieszkaniec wyspy nie mógł wypowiedzieć takiego zdania.
B) Obaj są kłamcami.
C) Abacki jest kłamcą, a Babacki jest rycerzem.
D) Obaj są rycerzami.
E) Abacki jest rycerzem, a Babacki jest kłamcą.
Od sześciennej drewnianej kostki odpiłowano wszystkie naroża, jak na rysunku obok. Ile krawędzi ma powstała bryła?
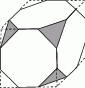
A) 48 B) 30 C) 24 D) 40 E) 36
Cyfrą jedności pewnej liczby trzycyfrowej jest 2. Jeżeli cyfrę tę przeniesiemy na początek tej liczby, to otrzymamy liczbę trzycyfrową o 36 mniejszą. Jaka jest suma cyfr tej liczby?
A) 1 B) 10 C) 7 D) 9 E) 5
Kasia rozłożyła 2007 pionków po równo do trzech pudełek 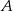 ,
, 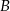 i
i 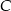 . Jeśli Kasia przełoży
. Jeśli Kasia przełoży  pionków z pudełka
pionków z pudełka 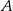 do pudełka
do pudełka 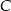 , to stosunek liczby pionków w pudełku
, to stosunek liczby pionków w pudełku 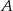 do liczby pionków w pudełku
do liczby pionków w pudełku 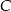 będzie równy
będzie równy
A) 1:2 B) 1:3 C) 2:3 D) 3:2 E) 1:5
Halina narysowała kwadrat o wymiarach 5x5 i zaznaczyła na rysunku środki kwadracików jednostkowych. Następnie umieściła przeszkody (pogrubione linie – patrz rysunek) i badała, na ile sposobów można przejść od punktu 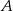 do punktu
do punktu 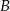 najkrótszą drogą, idąc pionowymi lub poziomymi odcinkami od środka kwadracika do środka kwadracika i omijając przeszkody. Ile jest takich najkrótszych dróg?
najkrótszą drogą, idąc pionowymi lub poziomymi odcinkami od środka kwadracika do środka kwadracika i omijając przeszkody. Ile jest takich najkrótszych dróg?

A) 6 B) 8 C) 9 D) 11 E) 12
W spotkaniu towarzyskim u Adama wzięło udział czterech chłopców i cztery dziewczyny. W czasie spotkania chłopcy tańczyli tylko z dziewczętami, a dziewczęta tylko z chłopcami. Po spotkaniu na pytanie: „z iloma różnymi osobami tańczyłeś w czasie spotkania”, chłopcy kolejno powiedzieli 3,1,2,2, natomiast trzy pierwsze dziewczęta podały liczby: 2,2,2. Z iloma chłopcami tańczyła czwarta dziewczyna?
A) 0 B) 1 C) 2 D) 3 E) 4
W parku wzdłuż alejki o długości 20m postanowiono po obu jej stronach posadzić krzewy róż. Zachowano przy tym zasadę, że odległość pomiędzy każdymi sąsiednimi krzewami po każdej stronie alejki jest równa 2m. Jaką maksymalną liczbę krzewów można posadzić wzdłuż tej alejki?
A) 22 B) 20 C) 12 D) 11 E) 10
Suma pewnych pięciu kolejnych liczb całkowitych jest równa sumie następnych trzech kolejnych liczb całkowitych. Największa z tych ośmiu liczb jest równa
A) 4 B) 8 C) 9 D) 11 E) 12
Na poniższym rysunku przedstawiona jest oś liczbowa z zaznaczonymi kolejnymi liczbami całkowitymi. Sześć z tych liczb oznaczono literami 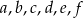 . Wiadomo, że co najmniej dwie z nich są podzielne przez 3 i co najmniej dwie z nich są podzielne przez 5. Które liczby są podzielne przez 15?
. Wiadomo, że co najmniej dwie z nich są podzielne przez 3 i co najmniej dwie z nich są podzielne przez 5. Które liczby są podzielne przez 15?
![]()
A)  i
i 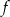 B)
B) 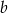 i
i  C)
C)  i
i 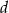 D) Wszystkie sześć E) Żadna z nich
D) Wszystkie sześć E) Żadna z nich
W pudełku znajduje się 7 kart. Na każdej z nich napisano dokładnie jedną z liczb od 1 do 7 i na różnych kartach, różne liczby. Mędrzec 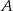 wyciągnął losowo 3 karty z pudełka, zaś mędrzec
wyciągnął losowo 3 karty z pudełka, zaś mędrzec 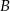 wyciągnął losowo 2 karty (w pudełku zostały dwie karty). Wówczas mędrzec
wyciągnął losowo 2 karty (w pudełku zostały dwie karty). Wówczas mędrzec 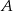 powiedział do mędrca
powiedział do mędrca 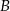 : „Wiem, że suma liczb na twoich kartach jest parzysta.” Suma liczb na kartach mędrca
: „Wiem, że suma liczb na twoich kartach jest parzysta.” Suma liczb na kartach mędrca 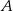 jest równa
jest równa
A) 10 B) 12 C) 6 D) 9 E) 15
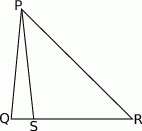
Na rysunku obok punkty 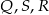 są współliniowe oraz
są współliniowe oraz 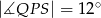 i
i 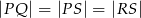 . Wówczas miara kąta
. Wówczas miara kąta 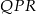 jest równa
jest równa
A) 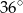 B)
B) 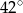 C)
C) 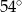 D)
D) 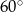 E)
E) 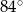
Powierzchnia bryły narysowanej obok składa się z 6 ścian trójkątnych. W każdym wierzchołku bryły umieszczono liczbę tak, by sumy liczb umieszczonych w wierzchołkach danej ściany były jednakowe dla wszystkich ścian. Dwie liczby 3 i 6 są zaznaczone na rysunku. Ile wynosi suma wszystkich liczb umieszczonych w wierzchołkach?
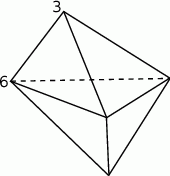
A) 9 B) 12 C) 17 D) 18 E) 24
Każdy z czterech kwadratów na rysunku ma bok długości 1. Jaka jest długość odcinka 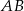 ?
?
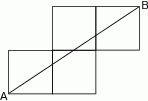
A) 5 B) 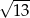 C)
C) 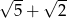 D)
D) 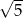 E) Inna odpowiedź
E) Inna odpowiedź
Trzema cięciami zaznaczonymi na rysunku podzielono duży sześcian na osiem prostopadłościanów. Ile jest równy stosunek sumy pól powierzchni tych ośmiu prostopadłościanów do pola powierzchni sześcianu?
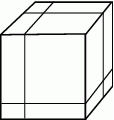
A) 1:1 B) 4:3 C) 3:2 D) 2:1 E) 4:1
Ile jest liczb naturalnych  , dla których największy spośród jej dzielników naturalnych różnych od 1 i
, dla których największy spośród jej dzielników naturalnych różnych od 1 i  jest 45 razy większy od najmniejszego spośród tych dzielników?
jest 45 razy większy od najmniejszego spośród tych dzielników?
A) 0 B) 1 C) 2 D) 3 E) Więcej niż 3.

