W pudełku 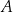 znajdowały się piłeczki, z których każda była w jednym z trzech kolorów: czerwonym, zielonym lub niebieskim. Liczby piłeczek czerwonych, zielonych i niebieskich znajdujących się w pudełku
znajdowały się piłeczki, z których każda była w jednym z trzech kolorów: czerwonym, zielonym lub niebieskim. Liczby piłeczek czerwonych, zielonych i niebieskich znajdujących się w pudełku 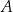 były – odpowiednio – kolejnymi liczbami podzielnymi przez 12. Połowę piłeczek czerwonych, połowę zielonych i połowę niebieskich przełożono do pojemnika
były – odpowiednio – kolejnymi liczbami podzielnymi przez 12. Połowę piłeczek czerwonych, połowę zielonych i połowę niebieskich przełożono do pojemnika 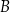 , a wszystkie piłeczki, które pozostały w pojemniku
, a wszystkie piłeczki, które pozostały w pojemniku 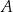 przełożono do pojemnika
przełożono do pojemnika 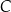 . Następnie, wszystkie piłeczki z pojemnika
. Następnie, wszystkie piłeczki z pojemnika 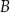 podzielono na 6 identycznych zestawów, a wszystkie piłeczki z pojemnika
podzielono na 6 identycznych zestawów, a wszystkie piłeczki z pojemnika 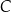 podzielono na 3 identyczne zestawy. Po dokonaniu tego podziału pokazało się, że w każdym zestawie utworzonym z piłeczek w pudełku
podzielono na 3 identyczne zestawy. Po dokonaniu tego podziału pokazało się, że w każdym zestawie utworzonym z piłeczek w pudełku 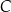 jest o 6 niebieskich piłeczek więcej, niż liczba piłeczek zielonych w zestawie utworzonym z piłeczek z pudełka
jest o 6 niebieskich piłeczek więcej, niż liczba piłeczek zielonych w zestawie utworzonym z piłeczek z pudełka 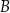 . Ile piłeczek czerwonych było początkowo w pudełku
. Ile piłeczek czerwonych było początkowo w pudełku 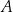 ?
?
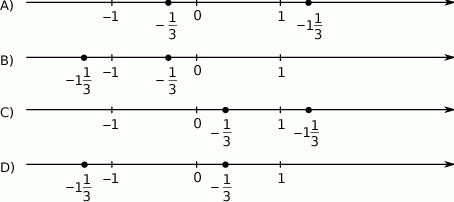
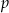 tak, jak na rysunku.
tak, jak na rysunku. 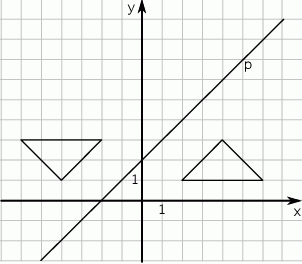
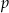 i osi
i osi 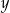 .
. 
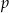 tak, jak na rysunku.
tak, jak na rysunku. 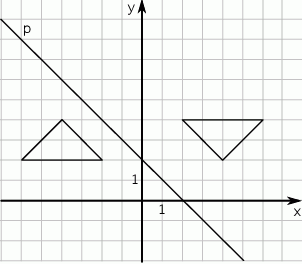
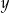
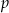
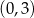
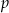 i osi
i osi 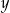 .
. 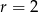 takie, że środek każdego z kół leży na brzegu drugiego koła. Oblicz pole powierzchni zacieniowanej części tej figury.
takie, że środek każdego z kół leży na brzegu drugiego koła. Oblicz pole powierzchni zacieniowanej części tej figury. 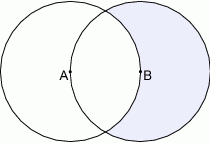
 i
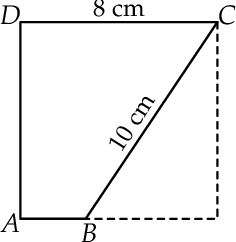
i 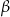 w trapezie przedstawionym na rysunku.
w trapezie przedstawionym na rysunku. 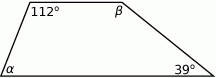
 i
i  w trapezie przedstawionym na rysunku.
w trapezie przedstawionym na rysunku. 
 i
i  w trapezie przedstawionym na rysunku.
w trapezie przedstawionym na rysunku. 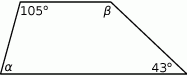
 i
i  w trapezie przedstawionym na rysunku.
w trapezie przedstawionym na rysunku. 
 podzielono na 3 równe części i połączono kolejno punkty podziału, w wyniku czego otrzymano ośmiokąt (rysunek).
podzielono na 3 równe części i połączono kolejno punkty podziału, w wyniku czego otrzymano ośmiokąt (rysunek). 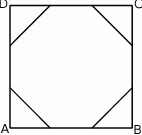
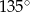 .
. 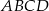 .
. 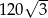 , a pole jego powierzchni całkowitej wynosi
, a pole jego powierzchni całkowitej wynosi 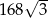 . Oblicz długość krawędzi podstawy i długość przekątnej ściany bocznej tego graniastosłupa. Zapisz obliczenia.
. Oblicz długość krawędzi podstawy i długość przekątnej ściany bocznej tego graniastosłupa. Zapisz obliczenia. 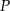 jest równe 4.
jest równe 4. 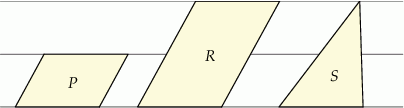
 jest równe 8.
jest równe 8. jest równe 4.
jest równe 4.  jest równe 4.
jest równe 4. 
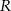 jest równe 12.
jest równe 12.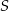 jest równe 8.
jest równe 8. 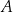 znajdowały się piłeczki, z których każda była w jednym z trzech kolorów: czerwonym, zielonym lub niebieskim. Liczby piłeczek czerwonych, zielonych i niebieskich znajdujących się w pudełku
znajdowały się piłeczki, z których każda była w jednym z trzech kolorów: czerwonym, zielonym lub niebieskim. Liczby piłeczek czerwonych, zielonych i niebieskich znajdujących się w pudełku 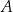 były – odpowiednio – kolejnymi liczbami podzielnymi przez 12. Połowę piłeczek czerwonych, połowę zielonych i połowę niebieskich przełożono do pojemnika
były – odpowiednio – kolejnymi liczbami podzielnymi przez 12. Połowę piłeczek czerwonych, połowę zielonych i połowę niebieskich przełożono do pojemnika 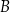 , a wszystkie piłeczki, które pozostały w pojemniku
, a wszystkie piłeczki, które pozostały w pojemniku 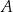 przełożono do pojemnika
przełożono do pojemnika 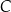 . Następnie, wszystkie piłeczki z pojemnika
. Następnie, wszystkie piłeczki z pojemnika 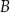 podzielono na 6 identycznych zestawów, a wszystkie piłeczki z pojemnika
podzielono na 6 identycznych zestawów, a wszystkie piłeczki z pojemnika 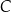 podzielono na 3 identyczne zestawy. Po dokonaniu tego podziału pokazało się, że w każdym zestawie utworzonym z piłeczek w pudełku
podzielono na 3 identyczne zestawy. Po dokonaniu tego podziału pokazało się, że w każdym zestawie utworzonym z piłeczek w pudełku 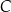 jest o 6 niebieskich piłeczek więcej, niż liczba piłeczek zielonych w zestawie utworzonym z piłeczek z pudełka
jest o 6 niebieskich piłeczek więcej, niż liczba piłeczek zielonych w zestawie utworzonym z piłeczek z pudełka 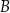 . Ile piłeczek czerwonych było początkowo w pudełku
. Ile piłeczek czerwonych było początkowo w pudełku 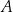 ?
? 
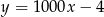
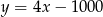
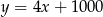
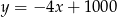
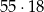 .
. 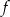 przyporządkowuje każdej liczbie ze zbioru
przyporządkowuje każdej liczbie ze zbioru 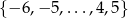 liczbę o 3 większą.
liczbę o 3 większą. 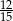 całej dostawy. Ile kilogramów mąki trzeba jeszcze dostarczyć do sklepu?
całej dostawy. Ile kilogramów mąki trzeba jeszcze dostarczyć do sklepu?  .
. 
 i
i  ?
?