Promień okręgu opisanego na prostokącie o bokach: 6 cm i 8 cm jest równy:
A) 7 cm B) 6,5 cm C) 5 cm D) 10 cm
/Szkoła podstawowa
Narysuj dowolny trójkąt oraz trójkąt do niego symetryczny:
- względem prostej zawierającej jeden z boków;
- względem prostej przecinającej dwa boki trójkąta;
- względem prostej zawierającej jedną z wysokości trójkąta.
Funkcja 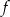 przyporządkowuje każdej liczbie ze zbioru
przyporządkowuje każdej liczbie ze zbioru 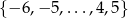 liczbę o 3 większą.
liczbę o 3 większą.
- Narysuj tabelkę, a następnie wykres tej funkcji.
- Zapisz wzór tej funkcji.
- Jaka jest najmniejsza, a jaka największa wartość tej funkcji?
- Ustal miejsca zerowe tej funkcji.
Do sklepu dostarczono 136 kg mąki, co stanowi 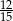 całej dostawy. Ile kilogramów mąki trzeba jeszcze dostarczyć do sklepu?
całej dostawy. Ile kilogramów mąki trzeba jeszcze dostarczyć do sklepu?
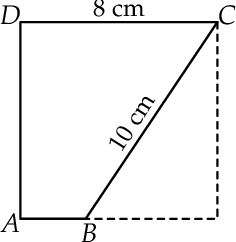
Z kwadratu o boku długości 8 cm wycięto trójkąt prostokątny o przeciwprostokątnej długości 10 cm w sposób pokazany na rysunku. Oblicz pole otrzymanego czworokąta 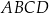 .
.
Pewien towar, obłożony 7–procentowym podatkiem VAT, kosztuje 1712 zł. O ile złotych wzrosłaby cena tego towaru, gdyby został on obłożony 22-procentowym podatkiem VAT?
Pewien towar, obłożony 8–procentowym podatkiem VAT, kosztuje 1296 zł. O ile złotych wzrosłaby cena tego towaru, gdyby został on obłożony 23-procentowym podatkiem VAT?
Na której osi liczbowej prawidłowo zaznaczono liczby 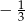 i
i 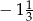 ?
?
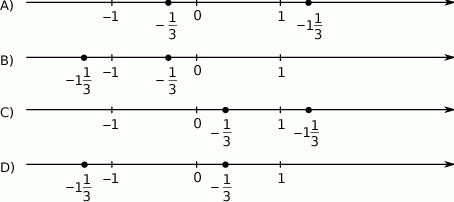
Tabela przedstawia funkcję określoną jednym z poniższych wzorów. Którym?
 | 1 | 2 | 3 | 4 |
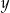 | 0 | 4 | 8 | 12 |
A) 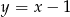 B)
B) 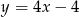 C)
C) 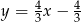 D)
D) 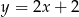
Tabela przedstawia funkcję określoną jednym z poniższych wzorów. Którym?
 | 1 | 2 | 3 | 4 |
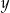 | 0 | 1 | 2 | 3 |
A) 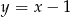 B)
B) 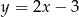 C)
C) 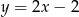 D)
D) 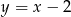
Tabela przedstawia funkcję określoną jednym z poniższych wzorów. Którym?
 | 1 | 2 | 3 | 4 |
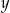 | 4 | 7 | 10 | 13 |
A) 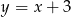 B)
B) 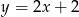 C)
C) 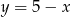 D)
D) 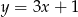
Jabłka i gruszki pakowano do pojemników, przy czym do jednego pojemnika wkładano 64 gruszki lub 80 jabłek. Po zapakowaniu owoców okazało się, że zapakowano dokładnie tyle samo jabłek, co gruszek.
Jaka jest najmniejsza możliwa liczba pojemników, do których zapakowano te owoce?
A) 5 B) 18 C) 9 D) 4
Jeśli długość jednego boku prostokąta zwiększymy o 20%, a długość drugiego boku prostokąta zmniejszymy o 5%, to pole prostokąta zwiększy się o:
A) 12% B) 14% C) 15% D) 16%
Jeśli długość jednego boku prostokąta zmniejszymy o 20%, a długość drugiego boku prostokąta zwiększymy o 5%, to pole prostokąta zmniejszy się o:
A) 12% B) 14% C) 15% D) 16%
Z drutu miedzianego o długości 11 metrów odcięto kawałek, którego długość mierzona w centymetrach jest równa długości pozostałej części drutu mierzonej w decymetrach. Oblicz długość odciętego kawałka drutu.
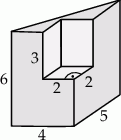
Bryła przedstawiona na poniższym rysunku powstała przez wycięcie z graniastosłupa prostego trójkątnego innego graniastosłupa prostego. Oblicz pole powierzchni i objętość tej bryły.
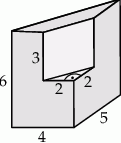
Bryła przedstawiona na poniższym rysunku powstała przez wycięcie z graniastosłupa prostego trójkątnego innego graniastosłupa prostego. Oblicz pole powierzchni i objętość tej bryły.
Wyznacz miejsce zerowe funkcji 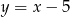 .
.
Znajdź miejsca zerowe funkcji 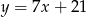 .
.
Znajdź miejsca zerowe funkcji 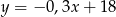 .
.
Znajdź miejsca zerowe funkcji 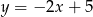 .
.
Znajdź miejsca zerowe funkcji 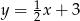 .
.
Jeżeli odcinek 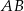 przecina oś
przecina oś 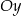 układu współrzędnych, to końce tego odcinka mogą mieć współrzędne
układu współrzędnych, to końce tego odcinka mogą mieć współrzędne
A) 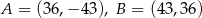 B)
B) 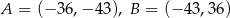
C) 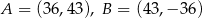 D)
D) 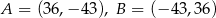
Na rysunku przedstawiono wykres pewnej funkcji.
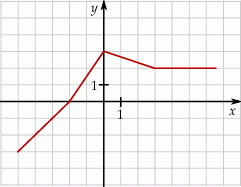
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Funkcja przyjmuje wartość 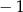 dla argumentu dla argumentu 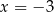 . . | P | F |
Dla wszystkich argumentów 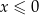 funkcja przyjmuje wartości ujemne. funkcja przyjmuje wartości ujemne. | P | F |
Na rysunku przedstawiono wykres pewnej funkcji.
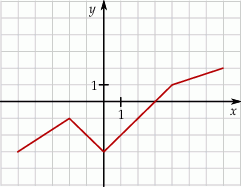
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Funkcja przyjmuje wartość 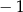 dla argumentu dla argumentu 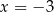 . . | P | F |
Dla wszystkich argumentów 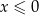 funkcja przyjmuje wartości ujemne. funkcja przyjmuje wartości ujemne. | P | F |
Na rysunku przedstawiono wykres pewnej funkcji.
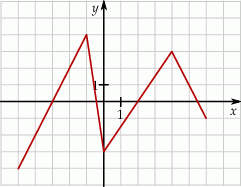
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Funkcja przyjmuje wartość 3 dla 4 argumentów. | P | F |
Dla wszystkich argumentów 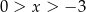 funkcja przyjmuje wartości dodatnie. funkcja przyjmuje wartości dodatnie. | P | F |
Ela i Ania dostały w prezencie po jednym zestawie puzzli o takiej samej liczbie elementów. Ela ułożyła  swoich puzzli, a Ania
swoich puzzli, a Ania 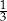 swoich. Dziewczynki ułożyły łącznie 440 elementów. Oblicz, z ilu elementów składa się jeden zestaw puzzli.
swoich. Dziewczynki ułożyły łącznie 440 elementów. Oblicz, z ilu elementów składa się jeden zestaw puzzli.
Napój otrzymano, po tym jak rozcieńczono 450 ml soku wodą w stosunku 1 : 10. Ile napoju otrzymano?
A) Więcej niż 4 litry, ale mniej niż 4,5 litra.
B) Dokładnie 4,5 litra.
C) Więcej niż 4,5 litra, ale mniej niż 5 litrów.
D) Dokładnie 5 litrów.
E) Więcej niż 5 litrów.
Na rysunku przedstawiono sześciokąt foremny o boku równym 2 cm. Przekątna 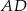 dzieli go na dwa przystające trapezy równoramienne.
dzieli go na dwa przystające trapezy równoramienne.
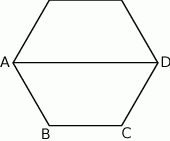
Wysokość trapezu 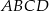 jest równa
jest równa
A) 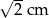 B)
B) 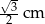 C)
C) 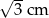 D) 2 cm
D) 2 cm
Na rysunku przedstawiono sześciokąt foremny 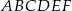 o boku równym 1 cm.
o boku równym 1 cm.
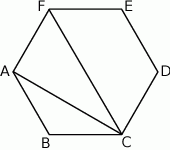
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Przekątna 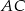 ma długość ma długość 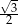 . . | P | F |
Przekątna 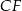 ma długość ma długość 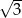 . . | P | F |
Na rysunku przedstawiono sześciokąt foremny o boku równym 4 cm. Przekątna 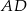 dzieli go na dwa przystające trapezy równoramienne.
dzieli go na dwa przystające trapezy równoramienne.
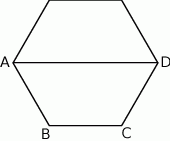
Pole trapezu 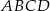 jest równe
jest równe
A) 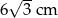 B)
B) 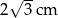 C)
C) 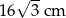 D)
D) 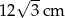
Pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego jest równe 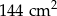 . Pole podstawy tej bryły stanowi 80% pola powierzchni bocznej tego ostrosłupa. Oblicz długość krawędzi podstawy tej bryły. Zapisz obliczenia.
. Pole podstawy tej bryły stanowi 80% pola powierzchni bocznej tego ostrosłupa. Oblicz długość krawędzi podstawy tej bryły. Zapisz obliczenia.
Znajdź liczbę, której 37% wynosi: 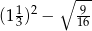 .
.

