Na rysunku przedstawiono graniastosłup 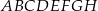 i ostrosłup
i ostrosłup 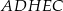 .
.
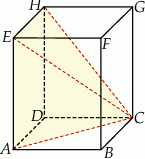
Objętość graniastosłupa jest większa od objętości ostrosłupa o 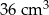 . Objętość ostrosłupa
. Objętość ostrosłupa 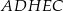 jest równa A/B.
jest równa A/B.
A) 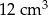 B)
B) 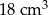
Objętość graniastosłupa 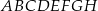 jest równa C/D.
jest równa C/D.
C) 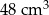 D)
D) 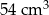
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na rysunku przedstawiono graniastosłup 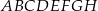 i ostrosłup
i ostrosłup 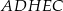 .
.

Objętość graniastosłupa jest większa od objętości ostrosłupa o 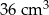 . Objętość ostrosłupa
. Objętość ostrosłupa 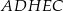 jest równa A/B.
jest równa A/B.
A) 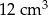 B)
B) 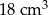
Objętość graniastosłupa 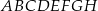 jest równa C/D.
jest równa C/D.
C) 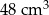 D)
D) 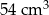
Na rysunku przedstawiono prostokąt 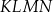 o bokach długości 24 cm i 10 cm.
o bokach długości 24 cm i 10 cm.

Czy wewnątrz tego prostokąta można umieścić odcinek 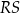 o długości
o długości 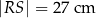 ? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | długość odcinka 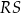 jest większa od długości odcinka jest większa od długości odcinka 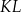 i większa od długości odcinka i większa od długości odcinka 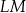 . . |
| B) | suma kwadratów długości odcinków 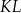 i i 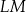 jest mniejsza niż kwadrat długości odcinka jest mniejsza niż kwadrat długości odcinka 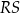 . . |
| C) | suma długości odcinków 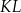 i i 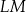 jest większa od długości odcinka jest większa od długości odcinka 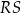 . . |
Na rysunku przedstawiono siatkę nietypowej sześciennej kostki do gry. Rzucamy jeden raz taką kostką.
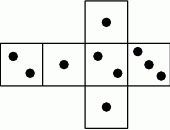
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wyrzucenia nieparzystej liczby oczek jest 2 razy większe niż prawdopodobieństwo wyrzucenia parzystej liczby oczek. | P | F |
Prawdopodobieństwo wyrzucenia liczby oczek mniejszej od 3 jest równe  . . | P | F |
Na rysunku przedstawiono siatkę nietypowej sześciennej kostki do gry. Rzucamy jeden raz taką kostką.

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wyrzucenia nieparzystej liczby oczek jest 2 razy większe niż prawdopodobieństwo wyrzucenia parzystej liczby oczek. | P | F |
Prawdopodobieństwo wyrzucenia liczby oczek mniejszej od 3 jest równe  . . | P | F |
Na rysunku przedstawiono siatkę nietypowej ośmiościennej kostki do gry. Rzucamy jeden raz taką kostką.
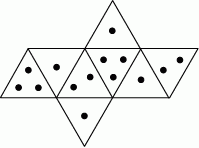
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wyrzucenia nieparzystej liczby oczek jest 3 razy większe niż prawdopodobieństwo wyrzucenia parzystej liczby oczek. | P | F |
Prawdopodobieństwo wyrzucenia liczby oczek większej od 1 jest równe 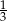 . . | P | F |
Na rysunku przedstawiono siatkę nietypowej dwunastościennej kostki do gry. Rzucamy jeden raz taką kostką.
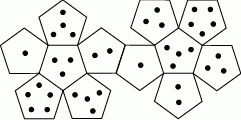
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wyrzucenia nieparzystej liczby oczek jest większe niż prawdopodobieństwo wyrzucenia parzystej liczby oczek. | P | F |
Prawdopodobieństwo wyrzucenia liczby oczek większej od 3 jest mniejsze od 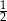 . . | P | F |
Dany jest prostokąt o wymiarach 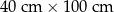 . Jeżeli każdy z dłuższych boków tego prostokąta wydłużymy o 20%, a każdy z krótszych boków skrócimy o 20%, to w wyniku obu przekształceń pole tego prostokąta
. Jeżeli każdy z dłuższych boków tego prostokąta wydłużymy o 20%, a każdy z krótszych boków skrócimy o 20%, to w wyniku obu przekształceń pole tego prostokąta
A) zwiększy się o 8% B) zwiększy się o 4%
C) zmniejszy się o 8% D) zmniejszy się o 4%
Dany jest prostokąt o wymiarach 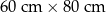 . Jeżeli każdy z dłuższych boków tego prostokąta wydłużymy o 10%, a każdy z krótszych boków skrócimy o 10%, to w wyniku obu przekształceń pole tego prostokąta
. Jeżeli każdy z dłuższych boków tego prostokąta wydłużymy o 10%, a każdy z krótszych boków skrócimy o 10%, to w wyniku obu przekształceń pole tego prostokąta
A) zwiększy się o 2% B) zwiększy się o 1%
C) zmniejszy się o 1% D) zmniejszy się o 2%
Długość przekątnej prostokąta przedstawionego na rysunku jest równa
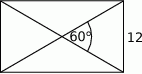
A) 12 B) 16 C) 20 D) 24
Suma kątów wewnętrznych pięciokąta foremnego jest równa
A) 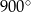 B)
B) 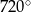 C)
C) 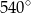 D)
D) 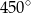
Na wycieczkę wyjechało 38 uczniów. Dzieci spały w 15 pokojach. Dziewczynki spały w pokojach dwuosobowych, a chłopcy spali w pokojach trzyosobowych. Wszystkie miejsca w pokojach były zajęte. Ile dziewczynek i ilu chłopców było na wycieczce? Zapisz obliczenia.
Każdy z 240 uczniów pewnej szkoły otrzymał 3 lub 4 darmowe bilety do kina. W sumie rozdano 880 biletów. Ilu uczniów otrzymało 3, a ilu 4 bilety? Zapisz obliczenia.
Przekątna w pewnym prostokącie jest 3 razy dłuższa niż krótszy bok tego prostokąta. W prostokącie do niego podobnym krótszy bok ma 1,5 cm. Jaką długość ma przekątna tego prostokąta?
W pewnej szkole do egzaminu gimnazjalnego przystąpiło o 60 chłopców więcej niż dziewcząt. Chłopcy stanowili 65% liczby osób piszących egzamin. Ile dziewcząt przystąpiło do tego egzaminu?
A) 200 B) 130 C) 70 D) 39
W pewnej szkole do egzaminu gimnazjalnego przystąpiło o 20 chłopców mniej niż dziewcząt. Chłopcy stanowili 45% liczby osób piszących egzamin. Ile dziewcząt przystąpiło do tego egzaminu?
A) 140 B) 110 C) 120 D) 90
Pewną kwotę rozdzielono na trzy nagrody pieniężne. Marcin dostał 2 razy więcej pieniędzy niż Jędrek, a Kamil 2 razy mniej niż Jędrek. Uzasadnij, że Kamil otrzymał 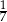 tej kwoty.
tej kwoty.
Pewną liczbę cukierków rozdzielono pomiędzy trzy osoby. Kasia otrzymała 3 razy mniej cukierków niż Zosia, a Ela 2 razy więcej niż Zosia. Uzasadnij, że Kasia otrzymała 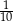 wszystkich cukierków.
wszystkich cukierków.
Spośród wszystkich liczb trzycyfrowych o sumie cyfr równej 6 wybrano liczbę największą i liczbę najmniejszą. Suma wybranych liczb jest równa
A) 714 B) 705 C) 606 D) 327
Spośród wszystkich liczb trzycyfrowych o sumie cyfr równej 7 wybrano liczbę największą i liczbę najmniejszą. Suma wybranych liczb jest równa
A) 806 B) 716 C) 860 D) 707
Poniżej zapisano trzy liczby:
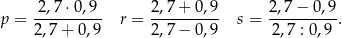
Który zapis przedstawia poprawnie uporządkowane liczby 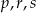 od najmniejszej do największej?
od najmniejszej do największej?
A) 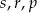 B)
B) 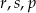 C)
C) 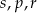 D)
D) 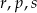
Na przedstawienie sprzedano 200 biletów po 25 zł i 35 zł. Po potrąceniu 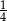 kwoty uzyskanej ze sprzedaży biletów na koszty związane z wynajęciem sali organizatorzy mieli 4650 zł zysku. Ile sprzedano biletów tańszych, a ile droższych ?
kwoty uzyskanej ze sprzedaży biletów na koszty związane z wynajęciem sali organizatorzy mieli 4650 zł zysku. Ile sprzedano biletów tańszych, a ile droższych ?
Na przedstawienie sprzedano 300 biletów po 15 zł i 20 zł. Po potrąceniu 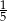 kwoty uzyskanej ze sprzedaży biletów na koszty związane z wynajęciem sali organizatorzy mieli 4176 zł zysku. Ile sprzedano biletów tańszych, a ile droższych ?
kwoty uzyskanej ze sprzedaży biletów na koszty związane z wynajęciem sali organizatorzy mieli 4176 zł zysku. Ile sprzedano biletów tańszych, a ile droższych ?
Wzrost podatku VAT z 7% do 22% spowodował wzrost ceny pewnego towaru o 5,55 zł. Cena tego towaru bez podatku VAT jest równa
A) 37 zł B) 39,59 zł C) 42,55 zł D) 25,23 zł
Wzrost podatku VAT z 7% do 22% spowodował wzrost ceny pewnego towaru o 6,45 zł. Cena tego towaru przed wprowadzeniem podatku VAT była równa
A) 5,48 zł B) 43 zł C) 49,45 zł D) 96,75 zł
Wzrost podatku VAT z 7% do 22% spowodował wzrost ceny pewnego towaru o 10,65 zł. Cena tego towaru przed wprowadzeniem podatku VAT była równa
A) 92,61 zł B) 12,25 zł C) 71 zł D) 81,65 zł
Ponumeruj poniższe czynności od 1 do 4 według kolejności prowadzącej do skonstruowania symetralnej odcinka 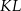 .
.
. . . . . Kreślimy okręgi o promieniu  i środkach w
i środkach w 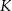 i
i 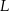 .
.
. . . . . Prowadzimy prostą przechodzącą przez punkty wspólne okręgów.
. . . . . Wybieramy odcinek  większy od połowy długości odcinka
większy od połowy długości odcinka 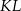 .
.
. . . . . Wyznaczamy punkty wspólne okręgów.
Janek ma 39 znaczków pocztowych w jednej kopercie i 16 w drugiej i chce dołożyć do każdej koperty tyle samo znaczków w tym celu, żeby w pierwszej było 2 razy więcej znaczków niż w drugiej. Po ile znaczków powinien dołożyć do każdej koperty?
Dane jest równanie
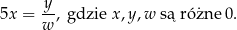
Zadaniem Pawła było przekształcanie tego równania tak, aby wyznaczyć 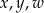 . Paweł otrzymał trzy równania:
. Paweł otrzymał trzy równania:
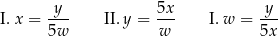
A) I i II B) II i III C) I i III D) I, II, III
Z urny, w której są wyłącznie kule białe, czarne i niebieskie losujemy 1 kulę.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Jeżeli prawdopodobieństwo wylosowania kuli białej jest równe prawdopodobieństwu wylosowania kuli, która nie jest biała, to prawdopodobieństwo wylosowania kuli niebieskiej jest równe  . . | P | F |
Jeżeli prawdopodobieństwo wylosowania kuli białej jest takie samo jak prawdopodobieństwo wylosowania kuli czarnej i jest równe 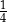 , to znaczy, że połowę wszystkich kul w urnie stanowią kule niebieskie. , to znaczy, że połowę wszystkich kul w urnie stanowią kule niebieskie. | P | F |
Narysowana poniżej figura składa się z kwadratu i trzech ćwiartek kół.
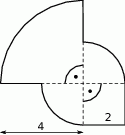
Pole tej figury jest równe
A) 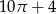 B)
B) 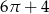 C)
C) 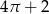 D)
D) 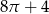
Brzeg narysowanej figury składa się 5 półokręgów.

Pole tej figury jest równe
A) 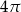 B)
B) 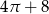 C)
C) 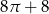 D)
D) 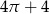
Narysowana poniżej figura składa się z kwadratu i trzech ćwiartek kół.
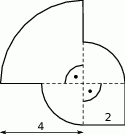
Obwód tej figury jest równy
A) 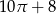 B)
B) 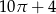 C)
C) 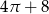 D)
D) 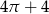
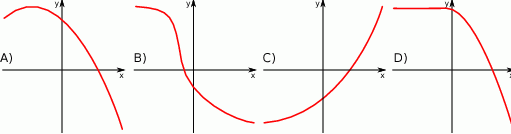
Który z wykresów przedstawia wykres funkcji rosnącej?
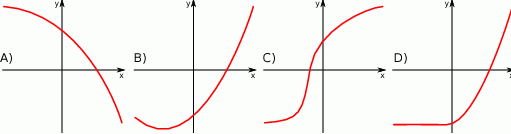
Który z wykresów przedstawia wykres funkcji malejącej?