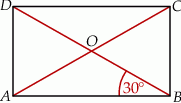
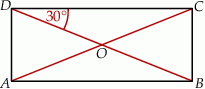
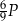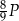W czworokącie 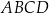 przekątne przecinają się w punkcie
przekątne przecinają się w punkcie 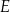 oraz
oraz 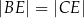 . Przekątna
. Przekątna 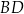 dzieli czworokąt
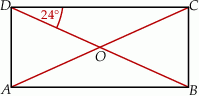
dzieli czworokąt 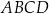 na trójkąt równoboczny i trójkąt równoramienny (zobacz rysunek).
na trójkąt równoboczny i trójkąt równoramienny (zobacz rysunek).
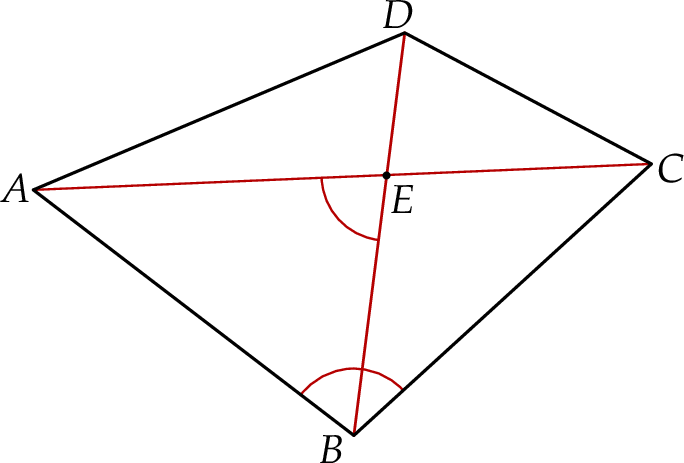
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąt 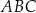 ma miarę ma miarę 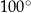 . . | P | F |
Kąt 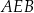 ma miarę ma miarę 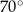 . . | P | F |


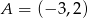 i
i 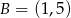 .
. 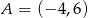 i
i 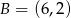 .
. 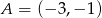 i
i 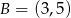 .
. 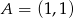 i
i 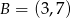 .
. 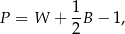
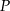 oznacza pole wielokąta,
oznacza pole wielokąta, 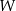 – liczbę punktów kratowych leżących wewnątrz wielokąta, a
– liczbę punktów kratowych leżących wewnątrz wielokąta, a 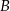 – liczbę punktów kratowych leżących na brzegu tego wielokąta.
– liczbę punktów kratowych leżących na brzegu tego wielokąta. 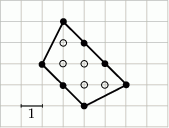
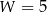 oraz
oraz 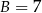 , zatem
, zatem 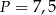 .
. 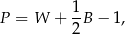
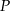 oznacza pole wielokąta,
oznacza pole wielokąta, 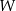 – liczbę punktów kratowych leżących wewnątrz wielokąta, a
– liczbę punktów kratowych leżących wewnątrz wielokąta, a 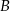 – liczbę punktów kratowych leżących na brzegu tego wielokąta.
– liczbę punktów kratowych leżących na brzegu tego wielokąta. 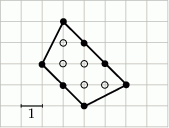
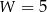 oraz
oraz 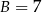 , zatem
, zatem 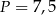 .
. 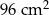
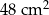
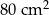
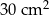
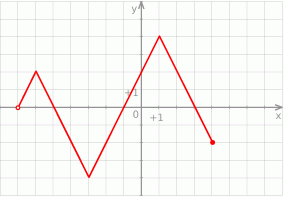
 .
. 
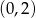 .
. 
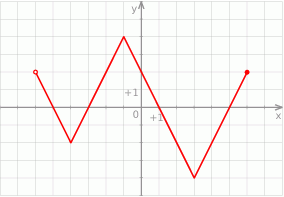
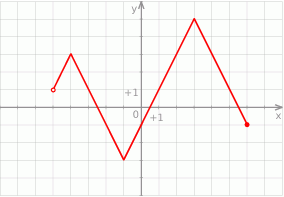
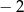 i 1.
i 1. 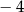 i jednocześnie mniejszych od 1 funkcja przyjmuje wartości ujemne.
i jednocześnie mniejszych od 1 funkcja przyjmuje wartości ujemne. 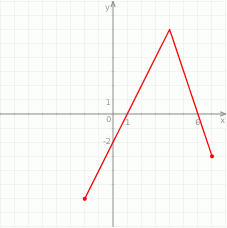
 . Sprawdź czy liczba
. Sprawdź czy liczba  należy do danego przedziału.
należy do danego przedziału.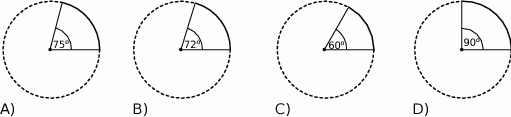
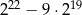 jest równa
jest równa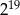
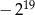
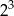
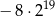
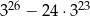 jest równa
jest równa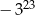
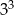
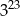
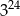
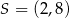 jest środkiem odcinka
jest środkiem odcinka 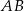 , gdzie
, gdzie 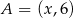 i
i 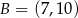 dla
dla  równego
równego 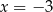
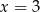
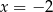
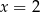
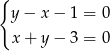 jest para
jest para 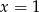 i
i 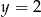
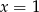 i
i 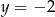
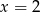 i
i 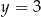
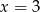 i
i 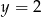
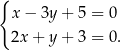
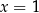 i
i 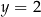
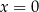 i
i 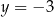
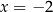 i
i 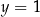
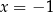 i
i 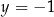
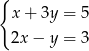 jest
jest 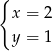
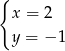
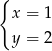
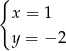
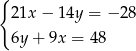 jest para liczb
jest para liczb 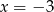 i
i 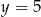
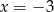 i
i 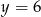
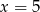 i
i 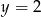
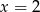 i
i 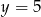
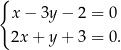
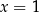 i
i 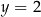
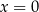 i
i 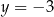
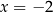 i
i 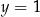
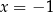 i
i 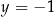
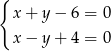 opisuje w układzie współrzędnych na płaszczyźnie punkt
opisuje w układzie współrzędnych na płaszczyźnie punkt 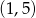
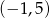
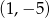
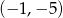
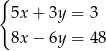 jest para liczb
jest para liczb 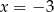 i
i 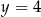
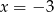 i
i 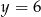
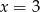 i
i 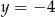
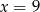 i
i 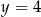
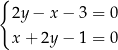 jest para
jest para 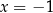 i
i 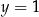
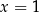 i
i 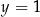
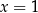 i
i 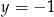
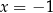 i
i 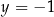
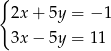 jest
jest 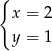
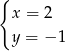
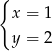
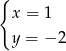
 , a jedna ściana boczna ma pole równe
, a jedna ściana boczna ma pole równe 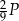 . Pole powierzchni bocznej tego ostrosłupa jest równe A/B.
. Pole powierzchni bocznej tego ostrosłupa jest równe A/B.