Beczka ma pojemność 67,2 litra, dzbanek - 1,6 litra, a kubek ma pojemność 5 razy mniejszą niż dzbanek. Napełnienie dzbanka wodą z kranu trwa 20 s, pokonanie drogi od kranu do beczki trwa 10 s i tyle samo trwa powrót do kranu. Wylewanie wody z dzbanka trwa 5 s.
- Ile czasu zajmie napełnienie beczki wodą za pomocą dzbanka?
- Ile czasu zajęłoby napełnienie beczki wodą za pomocą kubka? Przyjmijmy, że dojście do beczki i powrót do kranu z kubkiem w ręku trwa tyle samo, co z dzbankiem.
W obu sytuacjach należy przyjąć, że na początku i na końcu stoimy przy beczce.

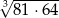 jest równa
jest równa 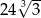
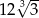
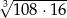 jest równa
jest równa 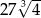
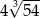
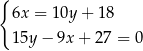
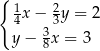
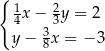
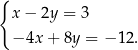
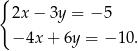
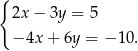
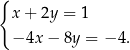
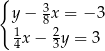
 kroków. Ile kroków zrobi Ewa w czasie 3 minut tego spaceru?
kroków. Ile kroków zrobi Ewa w czasie 3 minut tego spaceru?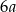
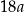
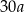
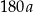
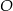 , który jest styczny do wszystkich boków trapezu równoramiennego
, który jest styczny do wszystkich boków trapezu równoramiennego 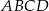 . Ramiona
. Ramiona 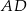 i
i 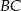 są styczne do tego okręgu odpowiednio w punktach
są styczne do tego okręgu odpowiednio w punktach 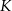 i
i 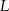 . Kąt wypukły
. Kąt wypukły 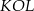 ma miarę
ma miarę 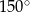 .
. 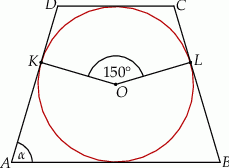
 kąta ostrego tego trapezu jest równa
kąta ostrego tego trapezu jest równa 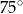
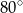
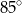
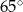
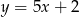 .
. 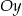 .
. 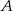 do wierzchołka będącego drugim końcem przekątnej sześcianu wychodzącej z wierzchołka
do wierzchołka będącego drugim końcem przekątnej sześcianu wychodzącej z wierzchołka 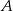 , przy czym była to droga najkrótsza. Narysuj siatkę sześcianu i oblicz odległość, jaką pokonała mrówka, jeżeli krawędź sześcianu ma długość
, przy czym była to droga najkrótsza. Narysuj siatkę sześcianu i oblicz odległość, jaką pokonała mrówka, jeżeli krawędź sześcianu ma długość 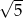 .
. 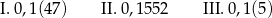
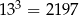 i
i 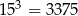 , oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
, oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe. 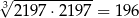
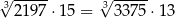
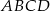 narysowano dwa półokręgi o średnicach
narysowano dwa półokręgi o średnicach 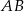 i
i 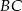 (patrz rysunek).
(patrz rysunek). 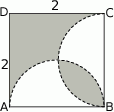
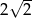
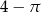
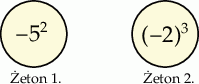
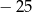 i
i 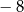
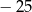 i 8
i 8 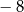
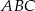 prowadzimy dwusieczną kąta
prowadzimy dwusieczną kąta 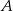 i przez punkt
i przez punkt 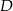 przecięcia się tej dwusiecznej z bokiem
przecięcia się tej dwusiecznej z bokiem 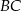 prowadzimy proste równoległe do boków
prowadzimy proste równoległe do boków 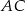 i
i 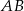 , które przecinają te boki odpowiednio w punktach
, które przecinają te boki odpowiednio w punktach 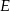 i
i 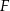 . Wykaż, że czworokąt
. Wykaż, że czworokąt 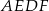 jest rombem. Czy można uogólnić to twierdzenie na dwusieczne kątów zewnętrznych?
jest rombem. Czy można uogólnić to twierdzenie na dwusieczne kątów zewnętrznych? 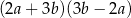 jest równe
jest równe 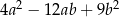
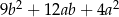
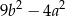
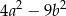
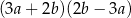 jest równe
jest równe 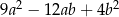
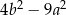
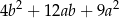
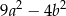
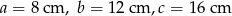 . Oblicz obwód trójkąta podobnego w skali 5.
. Oblicz obwód trójkąta podobnego w skali 5. 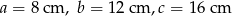 . Oblicz obwód trójkąta podobnego w skali
. Oblicz obwód trójkąta podobnego w skali 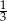 .
. 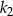 jest o 10% większa od długości boku kwadratu
jest o 10% większa od długości boku kwadratu 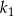 . Wówczas pole kwadratu
. Wówczas pole kwadratu 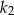 jest większe od pola kwadratu
jest większe od pola kwadratu 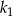 o
o