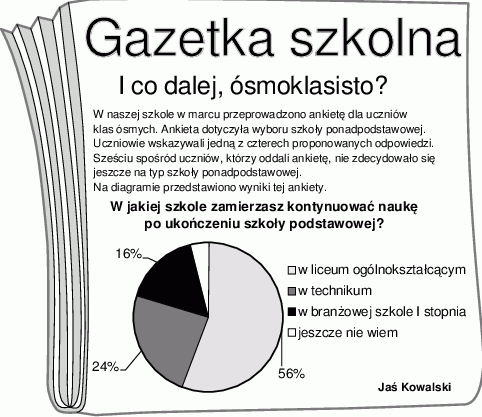
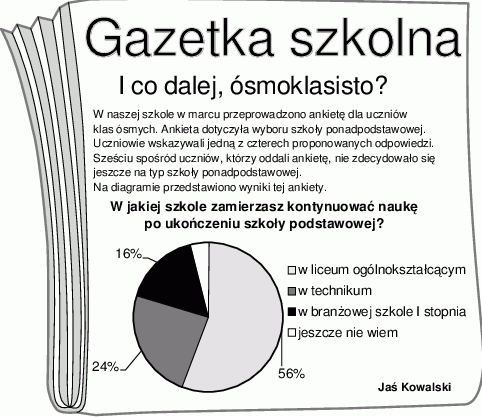
W szkole Adama w gazetce szkolnej ukazał się artykuł, dotyczący wyboru przez ósmoklasistów szkoły ponadpodstawowej.
Poniżej zapisano trzy prawdziwe informacje.
I. Ankietę oddało łącznie 150 uczniów.
II. W ankiecie wzięli udział wszyscy uczniowie klas ósmych.
III. Łącznie mniej niż połowa uczniów biorących udział w ankiecie zamierza kontynuować naukę w technikum lub w branżowej szkole.
Które z informacji – I, II, III – wynikają z analizy danych zamieszczonych w treści artykułu?
A) Tylko I i II. B) Tylko I i III. C) Tylko II i III. D) Wszystkie – I, II i III.
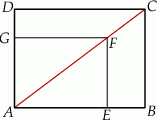
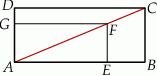
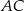 prostokąta
prostokąta 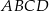 ma długość 70. Na boku
ma długość 70. Na boku 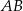 obrano punkt
obrano punkt 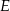 , na przekątnej
, na przekątnej 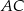 obrano punkt
obrano punkt 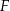 , a na boku
, a na boku 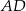 obrano punkt
obrano punkt 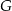 – tak, że czworokąt
– tak, że czworokąt 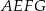 jest prostokątem (zobacz rysunek). Ponadto
jest prostokątem (zobacz rysunek). Ponadto 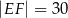 i
i 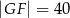 .
. 
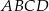 jest równy
jest równy 
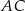 prostokąta
prostokąta 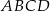 ma długość 104. Na boku
ma długość 104. Na boku 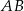 obrano punkt
obrano punkt 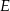 , na przekątnej
, na przekątnej 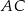 obrano punkt
obrano punkt 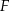 , a na boku
, a na boku 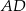 obrano punkt
obrano punkt 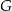 – tak, że czworokąt
– tak, że czworokąt 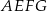 jest prostokątem (zobacz rysunek). Ponadto
jest prostokątem (zobacz rysunek). Ponadto 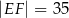 i
i 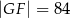 .
. 
 jest równy
jest równy 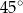 .
. 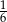 całej książki.
całej książki. 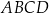 , w którym przekątna
, w którym przekątna 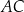 jest prostopadła do ramienia
jest prostopadła do ramienia 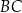 ,
, 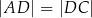 oraz
oraz 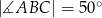 (zobacz rysunek).
(zobacz rysunek). 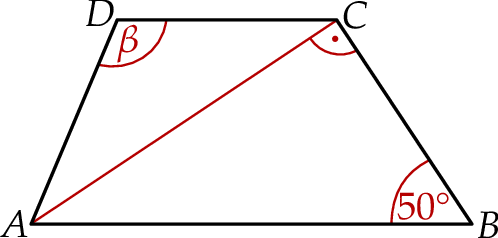
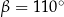
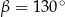
 , w którym bok
, w którym bok  jest równoległy do boku
jest równoległy do boku 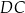 . W tym trapezie poprowadzono odcinek
. W tym trapezie poprowadzono odcinek 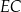 równoległy do boku
równoległy do boku 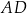 , podano miary dwóch kątów oraz oznaczono kąt
, podano miary dwóch kątów oraz oznaczono kąt  (zobacz rysunek).
(zobacz rysunek). 
 ma miarę
ma miarę 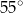
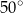
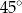
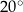
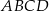 , w którym przekątna
, w którym przekątna 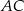 jest prostopadła do ramienia
jest prostopadła do ramienia 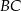 ,
, 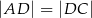 oraz
oraz 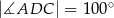 (zobacz rysunek).
(zobacz rysunek). 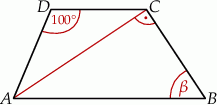
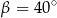
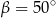
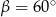
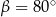
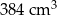 .
. 
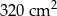
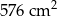
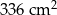
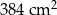
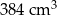 .
. 
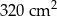
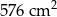
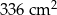
 i
i 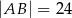 . Odcinek
. Odcinek 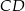 jest wysokością trójkąta
jest wysokością trójkąta 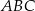 , a odcinek
, a odcinek 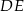 jest wysokością trójkąta
jest wysokością trójkąta 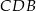 (zobacz rysunek).
(zobacz rysunek). 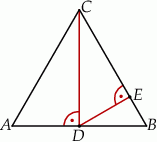
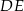 .
. 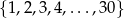 losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest kwadratem liczby całkowitej, jest równe
losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest kwadratem liczby całkowitej, jest równe 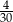
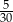
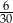
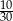
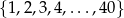 losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest kwadratem liczby całkowitej, jest równe
losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest kwadratem liczby całkowitej, jest równe 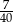
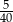
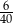
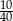
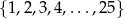 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby, która jest kwadratem liczby całkowitej, jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby, która jest kwadratem liczby całkowitej, jest równe 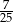
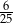
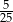
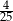
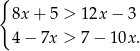
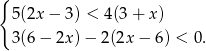
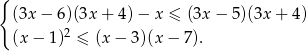
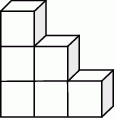
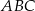 , w którym
, w którym 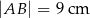 oraz odcinek
oraz odcinek 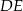 równoległy do boku
równoległy do boku  trójkąta, którego długość jest równa 6 cm.
trójkąta, którego długość jest równa 6 cm. 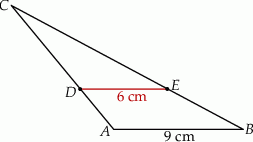
 jest równe
jest równe 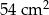 , a pole trapezu
, a pole trapezu 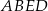 jest o 25% większe od pola trójkąta
jest o 25% większe od pola trójkąta 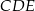 . Oblicz wysokość trapezu
. Oblicz wysokość trapezu 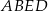 .
. 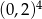
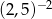
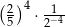
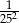
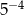 jest równa liczbom
jest równa liczbom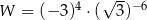 pomnożono przez 2. Wartość tego wyrażenia
pomnożono przez 2. Wartość tego wyrażenia 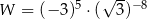 pomnożono przez 3. Wartość tego wyrażenia
pomnożono przez 3. Wartość tego wyrażenia 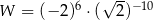 pomnożono przez 2. Wartość tego wyrażenia
pomnożono przez 2. Wartość tego wyrażenia 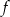 przyporządkowuje każdej liczbie naturalnej większej od 1 liczbę liczb pierwszych mniejszych od
przyporządkowuje każdej liczbie naturalnej większej od 1 liczbę liczb pierwszych mniejszych od  . Liczba
. Liczba 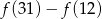 jest równa
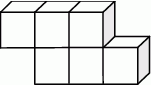
jest równa 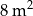 powierzchni?
powierzchni? 