Funkcja 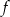 przyporządkowuje każdej liczbie naturalnej większej od 1 liczbę liczb pierwszych mniejszych od
przyporządkowuje każdej liczbie naturalnej większej od 1 liczbę liczb pierwszych mniejszych od  . Liczba
. Liczba 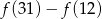 jest równa
jest równa
A) 5 B) 6 C) 4 D) 10
/Szkoła podstawowa
Ile kwadratowych płytek o boku 2 dm potrzeba do wyłożenia dna i wewnętrznych ścian basenu o długości 10 m, szerokości 6 m i głębokości 2 m ?
Objętość prostopadłościennego basenu o szerokości 6 m i długości 10 m jest równa 120 000 litrów. Ile litrów farby potrzeba do pomalowania dna i ścian basenu, jeżeli jeden litr farby wystarcza do pomalowania 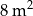 powierzchni?
powierzchni?
Ile kwadratowych płytek o boku 3 dm potrzeba do wyłożenia dna i wewnętrznych ścian basenu o długości 9 m, szerokości 6 m i głębokości 3 m ?
Podczas suszenia grzyby tracą 80% swojej masy. Ile ważą po wysuszeniu 2 kilogramy grzybów?
A) 0,20 kg B) 0,24 kg C) 0,4 kg D) 0,96 kg
Podczas suszenia grzyby tracą 80% swojej masy. Ile waży po wysuszeniu 1 kg grzybów?
A) 0,20 kg B) 0,24 kg C) 0,4 kg D) 0,96 kg
Podczas suszenia grzyby tracą 80% swojej masy. Ile waży po wysuszeniu 2,4 kg grzybów?
A) 0,40 kg B) 0,48 kg C) 0,8 kg D) 0,96 kg
Dotąd wydobyto ok. 120 tys. ton złota, z czego około 72 tys. ton znajduje się w rękach prywatnych. Jaki procent złota znajduje się w rękach prywatnych?
Dane są liczby: 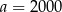 ,
, 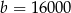 ,
, 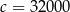 . Wartość wyrażenia
. Wartość wyrażenia 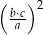 jest równa
jest równa
A) 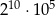 B)
B) 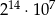 C)
C) 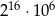 D)
D) 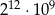
Liczby 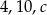 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
Liczby 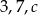 są długościami boków trójkąta równoramiennego. Oblicz długość boku
są długościami boków trójkąta równoramiennego. Oblicz długość boku  .
.
Liczby 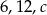 są długościami boków trójkąta równoramiennego. Oblicz długość boku
są długościami boków trójkąta równoramiennego. Oblicz długość boku  .
.
Pary liczb 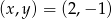 i
i 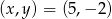 należą do zbioru rozwiązań układu równań
należą do zbioru rozwiązań układu równań
A) 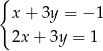 B)
B) 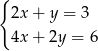 C)
C) 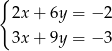 D)
D) 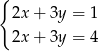
Pary liczb 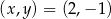 i
i 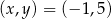 należą do zbioru rozwiązań układu równań
należą do zbioru rozwiązań układu równań
A) 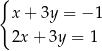 B)
B) 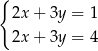 C)
C) 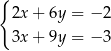 D)
D) 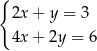
W kasie są banknoty 10–złotowe, 20–złotowe i 50–złotowe. Liczba banknotów 10–złotowych jest taka sama jak liczba banknotów 50–złotowych i o 32% mniejsza od liczby banknotów 20–złotowych. Łączna wartość wszystkich banknotów 10 i 20–złotowych jest o 540 złotych mniejsza od łącznej wartości wszystkich banknotów 50–złotowych. Oblicz, ile jest wszystkich banknotów w kasie.
Wszystkie wierzchołki czworokąta 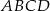 leżą na okręgu oraz
leżą na okręgu oraz 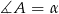 . Oblicz miarę kąta
. Oblicz miarę kąta 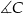 .
.
Do napełniania basenu służą dwa zawory. Jeżeli oba zawory są odkręcone jednocześnie, to basen napełnia się w ciągu 30 minut. Jeżeli odkręcony jest wyłącznie pierwszy zawór, to basen napełnia się w ciągu 66 minut. Jeżeli odkręcony jest wyłącznie drugi zawór, to basen napełnia się w ciągu A/B minut.
A) 60 B) 55
Objętość wody, która przepłynie przez zawór pierwszy w ciągu 6 minut jest taka sama jak objętość wody, która przepłynie przez zawór drugi w ciągu C/D minut.
C) 4 D) 5
Na rysunku przedstawiono fragment siatki graniastosłupa prawidłowego trójkątnego.
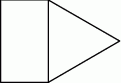
Pole narysowanego trójkąta jest równe 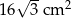 , a pole prostokąta jest równe
, a pole prostokąta jest równe 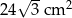 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
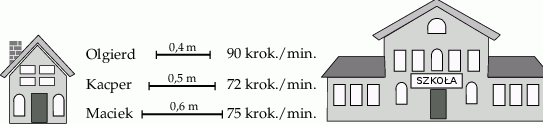
Trzech braci: Olgierd, Kacper i Maciek pokonują tę samą drogę z domu do szkoły. Olgierd stawia kroki długości 0,4 m w tempie 90 kroków na minutę, Kacper stawia kroki długości 0,5 m w tempie 72 kroków na minutę, a Maciek stawia kroki długości 0,6 m w tempie 75 kroków na minutę. Olgierd i Kacper przyszli do szkoły dokładnie w tym samym momencie, przy czym Kacper zrobił 900 kroków mniej od Olgierda. Oblicz, ile minut zajmie droga do szkoły Maćkowi.
Dane są liczby: 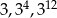 . Iloczyn tych liczb jest równy
. Iloczyn tych liczb jest równy
A) 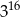 B)
B) 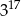 C)
C) 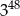 D)
D) 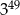
Dane są liczby: 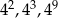 . Iloczyn tych liczb jest równy
. Iloczyn tych liczb jest równy
A) 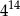 B)
B) 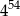 C)
C) 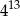 D)
D) 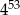
Na loterii jest 10 losów, z których 4 są wygrywające. Kupujemy jeden los. Prawdopodobieństwo zdarzenia, że nie wygramy nagrody, jest równe
A)  B)
B)  C)
C)  D)
D) 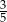
Na loterii jest 14 losów, z których 6 jest wygrywających. Kupujemy jeden los. Prawdopodobieństwo zdarzenia, że nie wygramy nagrody jest równe
A)  B)
B)  C)
C) 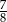 D)
D) 
W pudełku jest 50 kuponów, wśród których jest 15 kuponów przegrywających, a pozostałe kupony są wygrywające. Z tego pudełka w sposób losowy wyciągamy jeden kupon. Prawdopodobieństwo zdarzenia polegającego na tym, że wyciągniemy kupon wygrywający, jest równe
A) 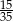 B)
B) 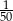 C)
C) 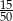 D)
D) 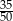
Na loterii jest 12 losów, z których 8 jest przegrywających. Kupujemy jeden los. Prawdopodobieństwo zdarzenia, że wygramy nagrodę jest równe
A) 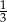 B)
B) 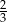 C)
C) 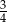 D)
D) 
Na loterii jest 20 losów, z których 8 jest wygrywających. Kupujemy jeden los. Prawdopodobieństwo zdarzenia, że nie wygramy nagrody jest równe
A) 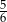 B)
B) 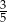 C)
C) 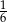 D)
D) 
W poniższej tabeli podano powierzchnię terytoriów (w milionach kilometrów kwadratowych), sześciu największych państw.
| Rosja | Kanada | USA | Chiny | Brazylia | Australia |
| 17,08 | 9,98 | 9,63 | 9,6 | 8,51 | 7,69 |
Powierzchnia lądów na Ziemi wynosi 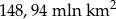 . Czy podane państwa zajmują w sumie ponad połowę powierzchni lądów? Oszacuj wyniki, nie wykonując dokładnych rachunków.
. Czy podane państwa zajmują w sumie ponad połowę powierzchni lądów? Oszacuj wyniki, nie wykonując dokładnych rachunków.
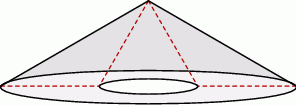
Trójkąt równoramienny o kącie 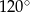 i ramieniu długości 6 obrócono względem zewnętrznej wysokości, otrzymując wydrążoną bryłę. Oblicz objętość tej bryły.
i ramieniu długości 6 obrócono względem zewnętrznej wysokości, otrzymując wydrążoną bryłę. Oblicz objętość tej bryły.
Oblicz pole powierzchni zacieniowanego odcinka koła.
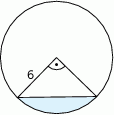
Oblicz pole powierzchni zacieniowanego odcinka koła.
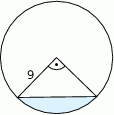
Oblicz pole powierzchni zacieniowanego odcinka koła.
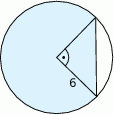
Oblicz pole powierzchni zacieniowanego odcinka koła.
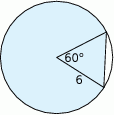
Oblicz pole powierzchni zacieniowanego odcinka koła.
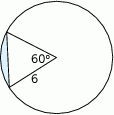
Oblicz: 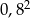 .
.
Oblicz: 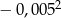 .
.
Oblicz: 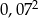 .
.
Oblicz: 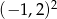 .
.
Oblicz: 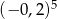 .
.
Oblicz: 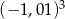 .
.
Oblicz: 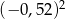 .
.
Oblicz: 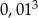 .
.
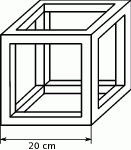
Na rysunku przedstawiono model sześcianu wykonany z listewek, których przekrój poprzeczny jest kwadratem o boku 2 cm. Krawędź sześcianu ma długość 20 cm. Oblicz jaka jest powierzchnia całkowita tego modelu. Zapisz obliczenia.
W trakcie przygotowań do zawodów pływackich Szymon i Bartosz pływali równolegle do brzegu jeziora na dystansie 2 km. Wykresy przedstawiają zależność między odległością chłopców od miejsca startu, a czasem pływania.
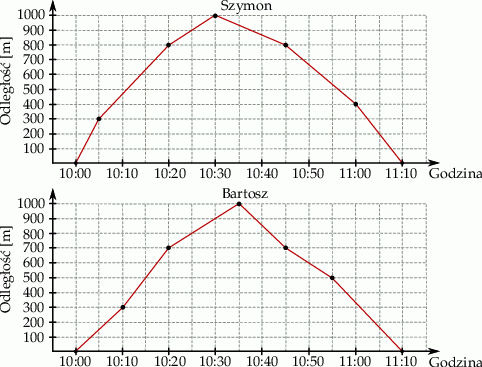
Ile razy między godziną 10:05 a 11:05 Szymon i Bartosz znajdowali się w tej samej odległości od miejsca startu?
A) 0 B) 1 C) 2 D) 4

