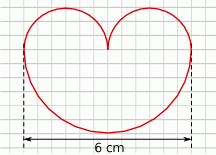
Oblicz jaką średnicę ma okrąg, którego długość jest równa długości figury przedstawionej na rysunku.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz jaką średnicę ma okrąg, którego długość jest równa długości figury przedstawionej na rysunku.

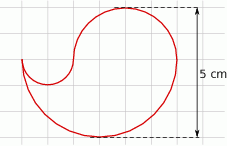
Oblicz jaki promień ma okrąg, którego długość jest równa długości figury przedstawionej na rysunku.
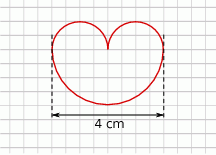
Oblicz jaką średnicę ma okrąg, którego długość jest równa długości figury przedstawionej na rysunku.
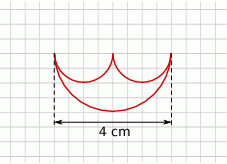
Oblicz jaką średnicę ma okrąg, którego długość jest równa długości figury przedstawionej na rysunku.
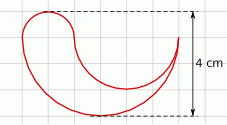
Oblicz jaką średnicę ma okrąg, którego długość jest równa długości figury przedstawionej na rysunku.
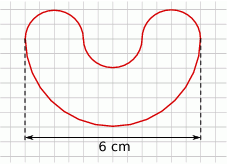
Oblicz jaki promień ma okrąg, którego długość jest równa długości figury przedstawionej na rysunku.
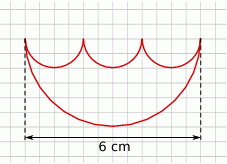
Oblicz długość figury przedstawionej na rysunku.
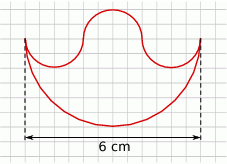
Oblicz długość figury przedstawionej na rysunku.
Graniastosłup prawidłowy czworokątny przecięto płaszczyzną, która zawiera krawędź podstawy oraz przechodzi przez środek przeciwległej krawędzi bocznej (zobacz rysunek).
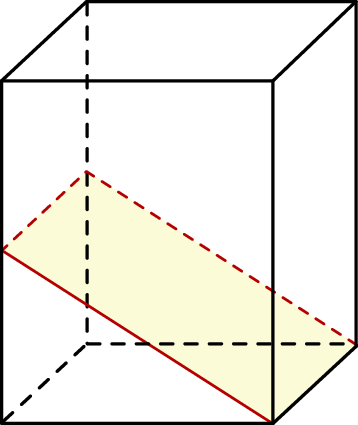
Oblicz jaki jest stosunek objętości dwóch brył na jakie został podzielony ten graniastosłup.
Przekrój osiowy stożka jest trójkątem równobocznym o polu 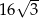 . Oblicz objętość i pole powierzchni całkowitej tego stożka.
. Oblicz objętość i pole powierzchni całkowitej tego stożka.
W pewnej klasie stosunek liczby dziewcząt do liczby chłopców jest równy 4:5. Losujemy jedną osobę z tej klasy. Prawdopodobieństwo tego, że będzie to dziewczyna, jest równe
A) 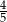 B)
B)  C)
C) 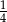 D)
D) 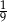
Średni wiek w pewnej sześcioosobowej grupie tematycznej na konferencji naukowej wynosił 49 lat. Najmłodszy uczestnik zrezygnował i wówczas średnia wieku wzrosła do 53 lat. Ile lat miał najmłodszy uczestnik?
Magda wydała na książkę połowę kwoty otrzymanej od mamy, a za 40% tego, co jej zostało, kupiła bilet do kina. Ile procent kwoty otrzymanej od mamy pozostało Magdzie?
A) 30% B) 60% C) 10% D) 20%
Andrzej połowę kwoty otrzymanej od taty przeznaczył na nową kurtkę, a 20% tego, co mu pozostało przeznaczył na bilet do kina. Ile procent kwoty otrzymanej od taty pozostało Andrzejowi?
A) 30% B) 80% C) 40% D) 20%
Na dwudziestu karteczkach napisano wszystkie liczby naturalne od 1 do 20 (na każdej karteczce napisano jedną liczbę). Spośród tych karteczek wybieramy w sposób losowy jedną. Niech 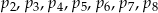 oznaczają prawdopodobieństwa, że na wylosowanej karteczce jest napisana liczba podzielna odpowiednio przez 2, 3, 4, 5, 6, 7, 8.
oznaczają prawdopodobieństwa, że na wylosowanej karteczce jest napisana liczba podzielna odpowiednio przez 2, 3, 4, 5, 6, 7, 8.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba  jest mniejsza od każdej z liczb: jest mniejsza od każdej z liczb:  . . | P | F |
Liczba 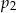 nie jest największą spośród liczb nie jest największą spośród liczb 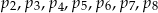 . . | P | F |
Wojtek miał 30 monet dwuzłotowych i 48 monet pięciozłotowych. Połowę monet pięciozłotowych wymienił na monety dwuzłotowe. Kwota z wymiany monet pięciozłotowych stanowiła równowartość kwoty, którą otrzymał w monetach dwuzłotowych. Oblicz, ile łącznie monet dwuzłotowych ma teraz Wojtek.
Która z figur ma większe pole: kwadrat o boku 8 cm, czy koło o średnicy 10 cm?
W pudełku znajdują się kule w trzech kolorach. Kul niebieskich jest o 30 więcej niż kul zielonych, a kul czerwonych jest o 70 więcej niż kul niebieskich. Kule zielone i czerwone stanowią 75% wszystkich kul znajdujących się w pudełku. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W pudełku jest cztery razy więcej kul niebieskich niż zielonych. | P | F |
| W pudełku jest 40 kul niebieskich. | P | F |
W układzie współrzędnych zaznaczono punkt 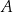 .
.

Punkt symetryczny do punktu 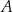 względem początku układu współrzędnych ma współrzędne
względem początku układu współrzędnych ma współrzędne
A) 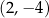 B)
B) 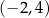 C)
C) 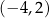 D)
D) 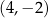
W układzie współrzędnych zaznaczono punkt 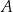 .
.

Punkt symetryczny do punktu 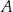 względem początku układu współrzędnych ma współrzędne
względem początku układu współrzędnych ma współrzędne
A) 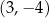 B)
B) 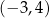 C)
C) 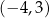 D)
D) 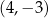
W fabryce zabawek znajduje się 10 maszyn do produkcji plastikowych samochodów. Średnia wydajność jednej maszyny wynosi 2100 samochodów dziennie. W okresie przedświątecznym uruchomiono jedną dodatkową maszynę, w wyniku czego średnia dzienna wydajność pojedynczego urządzenia zmalała o 4%. Oblicz ile samochodów dziennie produkuje dodatkowa maszyna.
Liczba  , która spełnia nierówność
, która spełnia nierówność 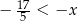
A) może być równa 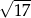 . B) może być równa 3,5.
. B) może być równa 3,5.
C) może być równa 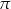 . D) może być dowolną liczbą dodatnią.
. D) może być dowolną liczbą dodatnią.
Liczba 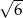 nie jest równa
nie jest równa
A) wysokości trójkąta równobocznego o boku długości 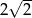
B) długości przekątnej kwadratu o boku długości 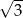
C) polu trójkąta równobocznego o boku długości 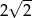
D) polu kwadratu o boku długości 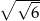
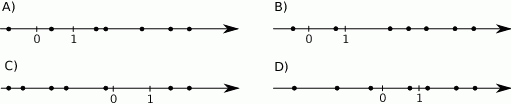
Na rysunkach przedstawiono osie liczbowe, a na każdej z nich kropkami zaznaczono siedem liczb.
Na którym rysunku jedna z tych liczb jest medianą pozostałych sześciu liczb?
W pudełku znajduje się 30 losów, w tym 5 losów wygrywających i 25 losów przegrywających. Po wyciągnięciu los nie jest zwracany do pudełka. Ania wybrała pięć losów i wszystkie były przegrywające. Po Ani jeden los wyciągnął Kuba.
Jakie jest prawdopodobieństwo, że Kuba wyciągnął los przegrywający?
A)  B)
B)  C)
C) 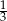 D)
D) 
W pudełku znajdowały się piłeczki białe i czarne – łącznie 72. Wśród wszystkich piłeczek 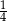 stanowiły piłeczki czarne. Wyciągnięto 12 piłeczek, wśród których żadna nie była czarna. Bartek – jako trzynasty – losuje jedną piłeczkę. Prawdopodobieństwo wylosowania przez Bartka piłeczki czarnej wynosi
stanowiły piłeczki czarne. Wyciągnięto 12 piłeczek, wśród których żadna nie była czarna. Bartek – jako trzynasty – losuje jedną piłeczkę. Prawdopodobieństwo wylosowania przez Bartka piłeczki czarnej wynosi
A) 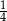 B)
B) 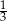 C)
C) 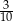 D)
D) 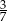
W pudełku znajdowały się piłeczki niebieskie i czerwone – łącznie 96. Wśród wszystkich piłeczek  stanowiły piłeczki czerwone. Wyciągnięto 16 piłeczek, wśród których żadna nie była czerwona. Kasia – jako siedemnasta – losuje jedną piłeczkę. Prawdopodobieństwo wylosowania przez Kasię piłeczki czerwonej wynosi
stanowiły piłeczki czerwone. Wyciągnięto 16 piłeczek, wśród których żadna nie była czerwona. Kasia – jako siedemnasta – losuje jedną piłeczkę. Prawdopodobieństwo wylosowania przez Kasię piłeczki czerwonej wynosi
A) 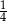 B)
B) 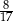 C)
C) 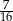 D)
D) 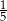
Cenę laptopa obniżono najpierw o 15%, a później o 150 zł. Po obu obniżkach laptop kosztuje 2400 zł.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Przed tymi dwoma obniżkami laptop kosztował 3000 zł. | P | F |
| Po obu obniżkach cena laptopa stanowi 85% ceny początkowej. | P | F |
Cenę roweru podwyższono najpierw o 35%, a później o 150 zł. Po obu podwyżkach rower kosztuje 4200 zł.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Przed tymi dwoma podwyżkami rower kosztował 3200 zł. | P | F |
| Po obu podwyżkach cena roweru stanowi 140% ceny początkowej. | P | F |
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Wartość wyrażenia 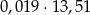 jest równa wartości wyrażenia jest równa wartości wyrażenia 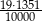 . . | P | F |
Wartość wyrażenia 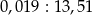 jest równa wartości wyrażenia jest równa wartości wyrażenia 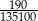 . . | P | F |
Do liczby 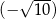 dodajemy 5. Otrzymany wynik jest liczbą
dodajemy 5. Otrzymany wynik jest liczbą
A) większą od 1. B) dodatnią mniejszą od 1.
C) mniejszą od 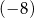 . D) ujemną większą od
. D) ujemną większą od 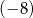 .
.
Do liczby 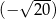 dodajemy 5. Otrzymany wynik jest liczbą
dodajemy 5. Otrzymany wynik jest liczbą
A) większą od 1. B) dodatnią mniejszą od 1.
C) mniejszą od 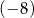 . D) ujemną większą od
. D) ujemną większą od 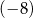 .
.
W pudełku było wyłącznie 216 kulek zielonych i 57 kulek niebieskich. Do tego pudełka dołożono pewną liczbę kulek niebieskich, a następnie usunięto tyle kulek zielonych, ile było kulek niebieskich w pudełku. Po tych zmianach prawdopodobieństwo wylosowania kulki niebieskiej jest równe  . Ile kulek zielonych usunięto z pudełka?
. Ile kulek zielonych usunięto z pudełka?
A) 87 B) 29 C) 144 D) 58
