Wiedząc, że funkcja określona jest wzorem 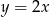 uzupełnij tabelkę, a następnie narysuj wykres tej funkcji.
uzupełnij tabelkę, a następnie narysuj wykres tej funkcji.
 | 1 | 2 | 3 | ||
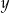 | 6 | 12 | 15 |
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wiedząc, że funkcja określona jest wzorem 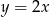 uzupełnij tabelkę, a następnie narysuj wykres tej funkcji.
uzupełnij tabelkę, a następnie narysuj wykres tej funkcji.
 | 1 | 2 | 3 | ||
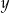 | 6 | 12 | 15 |
W trapezie prostokątnym 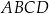 dane są długości podstaw
dane są długości podstaw 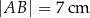 i
i 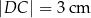 oraz długość ramienia prostopadłego do postaw
oraz długość ramienia prostopadłego do postaw 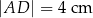 (zobacz rysunek).
(zobacz rysunek).
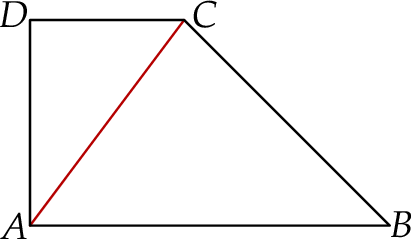
Oblicz odległość punktu 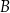 od przekątnej
od przekątnej 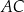 trapezu
trapezu 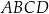 .
.
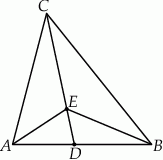
Na dwusiecznej 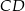 trójkąta
trójkąta 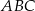 , w którym
, w którym 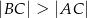 wybrano punkt
wybrano punkt 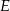 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 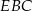 jest większe od pola trójkąta
jest większe od pola trójkąta 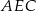 .
.
Dane są cztery wyrażenia:
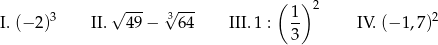
Największą wartość ma wyrażenie
A) I B) II C) III D) IV
Dane są trzy liczby:
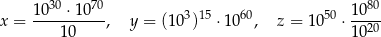
Która z tych liczb jest mniejsza od liczby 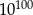 ?
?
A) Tylko  . B) Tylko
. B) Tylko 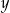 . C) Tylko
. C) Tylko  . D) Każda z liczb
. D) Każda z liczb 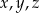 .
.
Dane są trzy liczby:
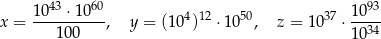
Która z tych liczb jest większa od liczby 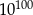 ?
?
A) Tylko  . B) Tylko
. B) Tylko  i
i 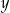 . C) Tylko
. C) Tylko 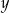 i
i  . D) Każda z liczb
. D) Każda z liczb 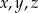 .
.
Ewa ma o 25% pieniędzy więcej niż Joasia. O ile procent Joasia ma mniej pieniędzy niż Ewa?
A) 25% B) 20% C) 50% D) 100%
Janek ma o 20% pieniędzy mniej niż Antek. O ile procent Antek ma więcej pieniędzy niż Janek?
A) 25% B) 20% C) 50% D) 100%
Oblicz pole trójkąta o wierzchołkach: 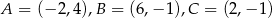 .
.
Oblicz pole trójkąta o wierzchołkach: 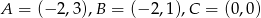 .
.
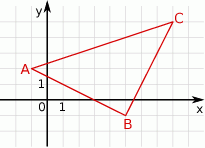
W układzie współrzędnych dane są punkty 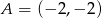 ,
, 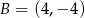 ,
, 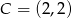 i
i 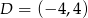 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Czworokąt 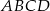 jest trapezem. jest trapezem. | P | F |
Czworokąt  posiada oś symetrii. posiada oś symetrii. | P | F |
Szklane naczynie w kształcie prostopadłościanu o wymiarach 6 cm, 15 cm i 18 cm napełniono częściowo wodą i szczelnie zamknięto. Następnie naczynie postawiono na jego ścianie o największej powierzchni i wtedy woda sięgała do wysokości 4 cm. Kiedy naczynie postawiono na ścianie o najmniejszej powierzchni, to woda sięgała do wysokości
A) 8 cm B) 10 cm C) 12 cm D) 16 cm
Szklane naczynie w kształcie prostopadłościanu o wymiarach 9 cm, 12 cm i 21 cm napełniono częściowo wodą i szczelnie zamknięto. Następnie naczynie postawiono na jego ścianie o największej powierzchni i wtedy woda sięgała do wysokości 6 cm. Kiedy naczynie postawiono na ścianie o najmniejszej powierzchni, to woda sięgała do wysokości
A) 8 cm B) 10 cm C) 12 cm D) 14 cm
Oblicz pole trójkąta przedstawionego na rysunku.
Wykonano następującą konstrukcję.
1. Narysowano trapez równoramienny  , w którym
, w którym 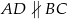 .
.
2. Wykreślono symetralne odcinków 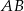 i
i 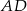 i ich punkt przecięcia oznaczono literą
i ich punkt przecięcia oznaczono literą 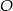 .
.
3. Narysowano okrąg o środku w punkcie 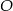 i promieniu
i promieniu 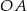 .
.
Skonstruowany w opisany powyżej sposób okrąg
A) przechodzi przez wszystkie wierzchołki tego trapezu.
B) jest styczny do wszystkich boków tego trapezu.
C) jest styczny do podstaw tego trapezu.
D) przechodzi przez środki ramion trapezu.
Małe trójkąty równoboczne o bokach długości 1 układano obok siebie tak, że uzyskiwano kolejne, coraz większe trójkąty równoboczne, według reguły przedstawionej na poniższym rysunku.
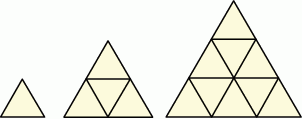
Ile małych trójkątów równobocznych należy użyć, aby ułożyć trójkąt równoboczny o podstawie równej 5?
A) 9 B) 16 C) 25 D) 50
Jeżeli 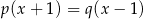 to
to
A) 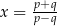 , gdy
, gdy 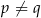 B)
B) 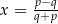 , gdy
, gdy 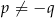
C) 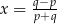 , gdy
, gdy 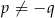 D)
D) 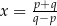 , gdy
, gdy 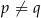
Jeżeli 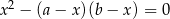 to
to
A) 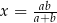 , gdy
, gdy 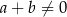 B)
B) 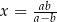 , gdy
, gdy 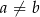
C) 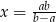 , gdy
, gdy 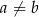 D)
D) 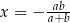 , gdy
, gdy 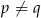
Dane są trzy wyrażenia:
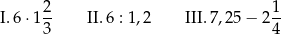
Liczbami całkowitymi są wartości wyrażeń
A) I, II i III B) Tylko I i II C) Tylko II i III D) Tylko I i III
Dane są trzy wyrażenia:
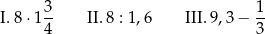
Liczbami całkowitymi są wartości wyrażeń
A) I, II i III B) Tylko I i II C) Tylko II i III D) Tylko I i III
Do akwarium z prostokątną podstawą o wymiarach 70 cm na 30 cm uczniowie włożyli dwukilogramowy kamień. Poziom wody podniósł się wówczas o 0,4 cm. Wykorzystując wyniki pomiarów oblicz masę 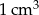 kamienia.
kamienia.
Na rysunkach I–IV przedstawiono cztery pary trójkątów.
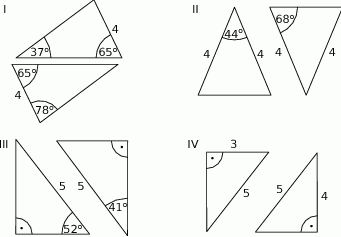
Na którym rysunku trójkąty nie są przystające?
A) I B) II C) III D) IV
Na rysunkach I–IV przedstawiono cztery pary trójkątów.
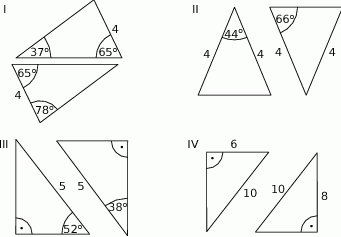
Na którym rysunku trójkąty nie są przystające?
A) I B) II C) III D) IV
Jakim procentem liczby której 1,5% wynosi 4 jest liczba która stanowi 33,3% liczby 12,6.
Zaokrąglij podane w tabelce długości najdłuższych rzek świata do dziesiątek kilometrów.
| Rzeka | Kontynent | Długość (w km) |
| Nil | Afryka | 6695 |
| Amazonka | Ameryka Płd. | 6437 |
| Jangcy | Azja | 6379 |
| Missisipi - Missouri | Ameryka Płn. | 6264 |
| Ob - Irtysz | Azja | 5411 |
| Huang - Ho | Azja | 4676 |
| Kongo | Afryka | 4667 |
Zaokrąglij podane w tabelce długości najdłuższych rzek świata do tysięcy kilometrów.
| Rzeka | Kontynent | Długość (w km) |
| Nil | Afryka | 6695 |
| Amazonka | Ameryka Płd. | 6437 |
| Jangcy | Azja | 6379 |
| Missisipi - Missouri | Ameryka Płn. | 6264 |
| Ob - Irtysz | Azja | 5411 |
| Huang - Ho | Azja | 4676 |
| Kongo | Afryka | 4667 |
Zaokrąglij podane w tabelce długości najdłuższych rzek świata do setek kilometrów.
| Rzeka | Kontynent | Długość (w km) |
| Nil | Afryka | 6695 |
| Amazonka | Ameryka Płd. | 6437 |
| Jangcy | Azja | 6379 |
| Missisipi - Missouri | Ameryka Płn. | 6264 |
| Ob - Irtysz | Azja | 5411 |
| Huang - Ho | Azja | 4676 |
| Kongo | Afryka | 4667 |
Kasia napisała na tablicy 6 kolejnych wielokrotności liczby 9. Uzasadnij, że suma pierwszych trzech z tych liczb jest o 81 mniejsza od sumy trzech ostatnich.
Pole powierzchni mieszkania jest równe 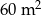 . Janek sporządził plan tego mieszkania. Jaką skalę zastosował Janek, jeśli pole powierzchni planu mieszkania było równe
. Janek sporządził plan tego mieszkania. Jaką skalę zastosował Janek, jeśli pole powierzchni planu mieszkania było równe 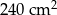 .
.
Wyznacz skalę mapy, na której jezioro o rzeczywistej powierzchni 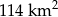 , zajmuje obszar
, zajmuje obszar 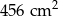 .
.
