Do 6 naczyń rozlano pewną ilość wody, przy czym do pierwszych czterech naczyń nalano łącznie tyle samo wody, ile do dwóch pozostałych.
Średnia arytmetyczna ilości wody w pierwszych czterech naczyniach
A) jest równa średniej ilości wody w dwóch ostatnich naczyniach
B) jest równa średniej ilości wody we wszystkich naczyniach
C) jest dwa razy mniejsza od średniej ilości wody w dwóch ostatnich naczyniach
D) jest dwa razy mniejsza od średniej ilości wody we wszystkich naczyniach
/Szkoła podstawowa
Hel używany jest do wypełniania balonów z powodu swej małej gęstości wynoszącej 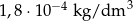 . Ile razy jest on lżejszy od powietrza, którego gęstość wynosi
. Ile razy jest on lżejszy od powietrza, którego gęstość wynosi 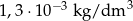 ?
?
Oblicz wysokość prostopadłościanu, którego podstawa jest prostokątem o wymiarach 3 i 4, a pole powierzchni całkowitej wynosi 94.
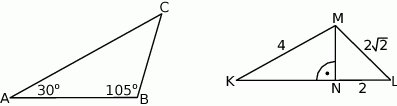
Uzasadnij, że trójkąty 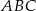 i
i 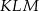 przedstawione na rysunku są podobne.
przedstawione na rysunku są podobne.
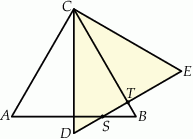
Trójkąty  i
i 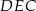 są przystającymi trójkątami równobocznymi o boku długości 6. Odcinki
są przystającymi trójkątami równobocznymi o boku długości 6. Odcinki 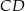 i
i 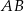 są prostopadłe, a odcinek
są prostopadłe, a odcinek 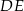 przecina odcinki
przecina odcinki 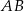 i
i 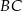 w punktach
w punktach 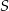 i
i 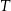 odpowiednio (zobacz rysunek). Oblicz długość odcinka
odpowiednio (zobacz rysunek). Oblicz długość odcinka 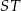 .
.
Wyrażenie 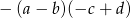 jest równe wyrażeniu
jest równe wyrażeniu
A) 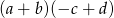 B)
B) 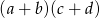 C)
C) 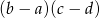 D)
D) 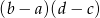
Album do zdjęć ma 21 stron. W albumie są 63 zdjęcia. Na każdej stronie jest taka sama liczba zdjęć. Które wyrażenie opisuje liczbę zdjęć znajdujących się na jednej stronie albumu?
A) 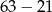 B)
B) 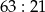 C)
C) 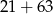 D)
D) 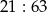
W równoległoboku 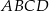 przekątna
przekątna 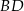 ma długość
ma długość 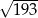 , a wysokość
, a wysokość 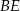 dzieli bok
dzieli bok 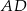 na odcinki o długościach
na odcinki o długościach 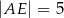 i
i 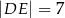 (zobacz rysunek).
(zobacz rysunek).
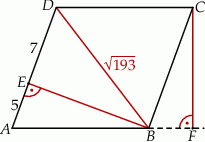
Oblicz długość wysokości 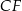 tego równoległoboku.
tego równoległoboku.
Średnia arytmetyczna zestawu liczb: 13, 16, 11, 4, 7, 9 zwiększy się o 25%, gdy w miejsce 7 wpiszemy liczbę
A) 75 B) 2,5 C) 15 D) 22
Średnia arytmetyczna zestawu liczb: 12, 5, 13, 9, 2, 7 zwiększy się o 75%, gdy w miejsce 2 wpiszemy liczbę
A) 36 B) 84 C) 38 D) 14
Do wykresu funkcji liniowej 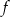 należą punkty
należą punkty 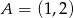 i
i 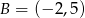 . Funkcja
. Funkcja 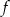 ma wzór
ma wzór
A) 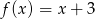 B)
B) 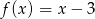 C)
C) 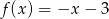 D)
D) 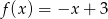
Do wykresu funkcji liniowej 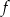 należą punkty
należą punkty 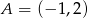 i
i 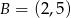 . Funkcja
. Funkcja 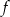 ma wzór
ma wzór
A) 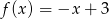 B)
B) 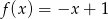 C)
C) 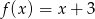 D)
D) 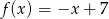
Do wykresu funkcji liniowej 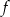 należą punkty
należą punkty 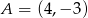 i
i 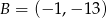 . Funkcja
. Funkcja 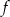 opisana jest wzorem
opisana jest wzorem
A) 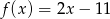 B)
B) 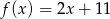 C)
C) 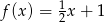 D)
D) 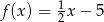
Do wykresu funkcji liniowej 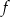 należą punkty
należą punkty 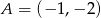 i
i 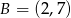 . Funkcja
. Funkcja 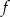 ma wzór
ma wzór
A) 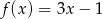 B)
B) 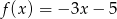 C)
C) 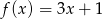 D)
D) 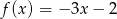
O funkcji liniowej 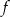 wiadomo, że
wiadomo, że 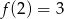 oraz punkt
oraz punkt 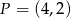 należy do jej wykresu. Wzór funkcji
należy do jej wykresu. Wzór funkcji 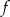 to
to
A) 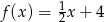 B)
B) 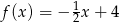 C)
C) 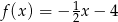 D)
D) 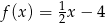
O funkcji liniowej 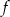 wiadomo, że
wiadomo, że 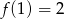 . Do wykresu tej funkcji należy punkt
. Do wykresu tej funkcji należy punkt 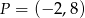 . Wzór funkcji
. Wzór funkcji 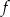 to
to
A) 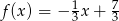 B)
B) 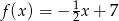 C)
C) 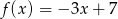 D)
D) 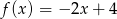
O funkcji liniowej 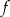 wiadomo, że
wiadomo, że 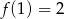 . Do wykresu tej funkcji należy punkt
. Do wykresu tej funkcji należy punkt 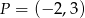 . Wzór funkcji
. Wzór funkcji 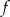 to
to
A) 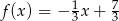 B)
B) 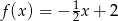 C)
C) 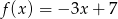 D)
D) 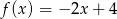
Przez punkty 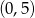 i
i 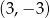 przechodzi wykres funkcji
przechodzi wykres funkcji
A) 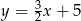 B)
B) 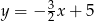 C)
C) 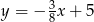 D)
D) 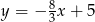
Przez punkty 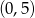 i
i 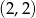 przechodzi wykres funkcji
przechodzi wykres funkcji
A) 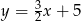 B)
B) 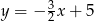 C)
C) 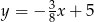 D)
D) 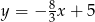
Przez punkty 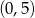 i
i 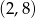 przechodzi wykres funkcji
przechodzi wykres funkcji
A) 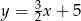 B)
B)  C)
C) 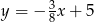 D)
D) 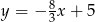
Podczas gotowania potrawa traci 60% zawartości witaminy C, 10% witaminy 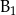 i po 5% witamin
i po 5% witamin 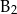 i E.
i E.
| Witamina | Zapotrzebowanie (w mg) |
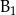 | 1,6 |
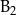 | 1,5 |
| E | 13 |
| C | 60 |
Oblicz na podstawie tabeli, ile tych witamin powinna zawierać potrawa przed gotowaniem, aby po przyrządzeniu mogła zaspokoić dzienne zapotrzebowanie na witaminy.
Oblicz pole powierzchni całkowitej i objętość prostopadłościanu 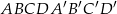 , w którym krawędź
, w którym krawędź 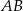 ma długość 10 cm i tworzy z przekątną
ma długość 10 cm i tworzy z przekątną 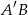 ściany bocznej kąt
ściany bocznej kąt 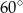 , a krawędź
, a krawędź 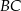 jest o cztery centymetry krótsza od krawędzi
jest o cztery centymetry krótsza od krawędzi 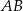 .
.
Liczba 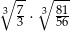 jest równa
jest równa
A) 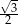 B)
B) 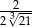 C)
C)  D)
D) 
Wartość wyrażenia 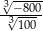 jest równa
jest równa
A) 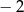 B)
B) 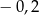 C) 2 D) 0,2
C) 2 D) 0,2
Liczba 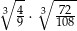 jest równa
jest równa
A)  B)
B) 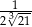 C)
C) 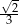 D)
D) 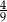
Liczba 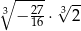 jest równa
jest równa
A) 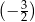 B)
B)  C)
C)  D)
D) 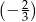
Liczba 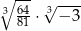 jest równa
jest równa
A) 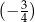 B)
B) 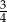 C)
C) 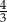 D)
D) 
Liczba 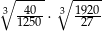 jest równa
jest równa
A) 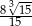 B)
B) 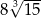 C) 8 D)
C) 8 D) 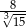
Z kartonu wykonano modele sześcianu i graniastosłupa prawidłowego czworokątnego. Podstawa sześcianu jest taka sama jak podstawa graniastosłupa. Na wykonanie sześcianu zużyto 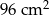 kartonu, a na graniastosłup o
kartonu, a na graniastosłup o 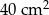 więcej (nie wliczając powierzchni zakładek).
więcej (nie wliczając powierzchni zakładek).
Korzystając z powyższych informacji, oceń prawdziwość poniższych zdań (P – prawda, F – fałsz).
Na wykonanie jednej ściany sześcianu zużyto 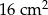 kartonu. kartonu. | P | F |
| Podstawą każdej z tych brył jest kwadrat o boku 4 cm. | P | F |
Pole powierzchni bocznej graniastosłupa jest równe 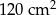 . . | P | F |
| Wysokość graniastosłupa jest równa 6 cm. | P | F |
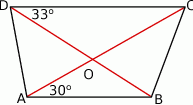
Oblicz miarę kąta ostrego pod którym przecinają się przekątne trapezu przedstawionego na rysunku.
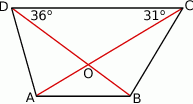
Oblicz miarę kąta ostrego pod którym przecinają się przekątne trapezu przedstawionego na rysunku.
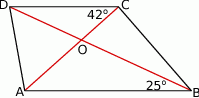
Oblicz miarę kąta ostrego pod którym przecinają się przekątne trapezu przedstawionego na rysunku.
W pudełku znajduje się 14 par skarpetek, w tym 8 par skarpetek czerwonych i 6 par skarpetek niebieskich. Ania losowo wybiera z pojemnika 14 skarpetek. Prawdopodobieństwo, że Ania wybrała co najmniej dwie skarpetki czerwone jest równe
A) 1 B) 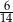 C)
C)  D)
D) 
Ośmiościan foremny jest bryłą zbudowaną z ośmiu przystających trójkątów równobocznych (zobacz rysunek).
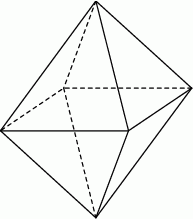
Oblicz objętość i pole powierzchni ośmiościanu foremnego, którego krawędź ma długość 6 cm.
Uzasadnij, że kąt ostry między dwusiecznymi kątów ostrych trójkąta prostokątnego jest równy 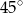 .
.
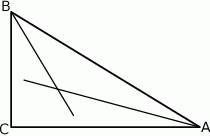
Uzasadnij, że trójkąty prostokątne 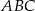 i
i 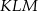 przedstawione na rysunku są podobne.
przedstawione na rysunku są podobne.
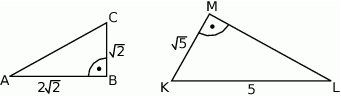
Największy wspólny dzielnik liczb 120 i 180, to
A) 90 B) 20 C) 30 D) 60

